Çoklu doğrusal regresyonun beş varsayımı
Çoklu doğrusal regresyon, birden fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz istatistiksel bir yöntemdir.
Ancak çoklu doğrusal regresyon gerçekleştirmeden önce ilk olarak beş varsayımın karşılandığından emin olmalıyız:
1. Doğrusal ilişki: Her yordayıcı değişken ile yanıt değişkeni arasında doğrusal bir ilişki vardır.
2. Çoklu doğrusallığın olmaması: yordayıcı değişkenlerin hiçbiri birbiriyle yüksek düzeyde korelasyona sahip değildir.
3. Bağımsızlık: Gözlemler bağımsızdır.
4. Homoskedastisite: artıklar doğrusal modelin her noktasında sabit bir varyansa sahiptir.
5. Çok değişkenli normallik: Model artıkları normal dağılıma sahiptir.
Bu varsayımlardan bir veya birkaçı karşılanmazsa çoklu doğrusal regresyon sonuçları güvenilir olmayabilir.
Bu yazıda her bir varsayım için bir açıklama, varsayımın karşılanıp karşılanmadığının nasıl belirleneceği ve varsayım karşılanmazsa ne yapılacağına dair açıklamalar sunuyoruz.
Hipotez 1: Doğrusal ilişki
Çoklu doğrusal regresyon, her yordayıcı değişken ile yanıt değişkeni arasında doğrusal bir ilişki olduğunu varsayar.
Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir
Bu varsayımın karşılanıp karşılanmadığını belirlemenin en basit yolu, her öngörücü değişkenin ve yanıt değişkeninin bir dağılım grafiğini oluşturmaktır.
Bu, iki değişken arasında doğrusal bir ilişki olup olmadığını görsel olarak görmenizi sağlar.
Dağılım grafiğindeki noktalar yaklaşık olarak düz bir çapraz çizgi boyunca uzanıyorsa değişkenler arasında muhtemelen doğrusal bir ilişki vardır.
Örneğin, aşağıdaki grafikteki noktaların düz bir çizgi üzerinde düşmesi, bu özel yordayıcı değişken (x) ile yanıt değişkeni (y) arasında doğrusal bir ilişki olduğunu gösterir:
Bu varsayıma uyulmazsa ne yapılmalı?
Bir veya daha fazla yordayıcı değişken ile yanıt değişkeni arasında doğrusal bir ilişki yoksa, birkaç seçeneğimiz vardır:
1. Tahmin değişkenine, örneğin log veya karekök alarak doğrusal olmayan bir dönüşüm uygulayın. Bu çoğu zaman ilişkiyi daha doğrusal bir ilişkiye dönüştürebilir.
2. Modele başka bir yordayıcı değişken ekleyin. Örneğin, x’e karşı y grafiği parabolik bir şekle sahipse, modele ek bir tahmin değişkeni olarak X2’yi eklemek mantıklı olabilir.
3. Tahmin değişkenini modelden çıkarın. En uç durumda, belirli bir yordayıcı değişken ile yanıt değişkeni arasında doğrusal bir ilişki yoksa, yordayıcı değişkenin modele dahil edilmesi yararlı olmayabilir.
Hipotez 2: çoklu bağlantı yok
Çoklu doğrusal regresyon, yordayıcı değişkenlerden hiçbirinin birbiriyle yüksek düzeyde korelasyona sahip olmadığını varsayar.
Bir veya daha fazla yordayıcı değişken yüksek düzeyde korelasyona sahip olduğunda, regresyon modeli çoklu doğrusallıktan muzdarip olur ve bu da modelin katsayı tahminlerini güvenilmez hale getirir.
Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir
Bu varsayımın karşılanıp karşılanmadığını belirlemenin en basit yolu, her bir yordayıcı değişken için VIF değerini hesaplamaktır.
VIF değerleri 1’den başlar ve üst sınırı yoktur. Genellikle 5*’in üzerindeki VIF değerleri potansiyel çoklu doğrusallığı gösterir.
Aşağıdaki eğitimler, çeşitli istatistiksel yazılımlarda VIF’nin nasıl hesaplanacağını gösterir:
*Bazen araştırmacılar, çalışma alanına bağlı olarak bunun yerine 10 VIF değerini kullanırlar.
Bu varsayıma uyulmazsa ne yapılmalı?
Bir veya daha fazla yordayıcı değişkenin VIF değeri 5’ten büyükse, bu sorunu çözmenin en kolay yolu, yüksek VIF değerlerine sahip yordayıcı değişkeni/değişkenleri kaldırmaktır.
Alternatif olarak, her bir tahmin değişkenini modelde tutmak istiyorsanız, yüksek korelasyonlu tahmin değişkenlerini ele almak üzere tasarlanmış ridge regresyonu , kement regresyonu veya kısmi en küçük kareler regresyonu gibi farklı bir istatistiksel yöntem kullanabilirsiniz.
Hipotez 3: Bağımsızlık
Çoklu doğrusal regresyon, veri setindeki her gözlemin bağımsız olduğunu varsayar.
Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir
Bu varsayımın karşılanıp karşılanmadığını belirlemenin en basit yolu, artıkların (ve dolayısıyla gözlemlerin) otokorelasyon sergileyip sergilemediğini bize söyleyen resmi bir istatistiksel test olan Durbin-Watson testini gerçekleştirmektir.
Bu varsayıma uyulmazsa ne yapılmalı?
Bu varsayımın nasıl ihlal edildiğine bağlı olarak birkaç seçeneğiniz vardır:
- Pozitif seri korelasyon için bağımlı ve/veya bağımsız değişkenin gecikmelerini modele eklemeyi düşünün.
- Negatif seri korelasyon için değişkenlerinizden hiçbirinin aşırı gecikmediğinden emin olun.
- Mevsimsel korelasyon için modele mevsimsel kuklalar eklemeyi düşünün.
Hipotez 4: Eşvaranlık
Çoklu doğrusal regresyon, artıkların doğrusal modeldeki her noktada sabit varyansa sahip olduğunu varsayar. Durum böyle olmadığında, artıklar değişen varyanstan muzdariptir.
Bir regresyon analizinde değişen varyans mevcut olduğunda, regresyon modelinin sonuçları güvenilmez hale gelir.
Spesifik olarak, heteroskedastisite, regresyon katsayısı tahminlerinin varyansını arttırır, ancak regresyon modeli bunu hesaba katmaz. Bu, gerçekte öyle olmadığı halde, bir regresyon modelinin, modeldeki bir terimin istatistiksel olarak anlamlı olduğunu iddia etme olasılığını çok daha artırır.
Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir
Bu varsayımın karşılanıp karşılanmadığını belirlemenin en kolay yolu, standartlaştırılmış artıkların tahmin edilen değerlere karşı bir grafiğini oluşturmaktır.
Bir veri kümesine bir regresyon modeli yerleştirdikten sonra, yanıt değişkeninin tahmin edilen değerlerini x ekseninde ve modelin standartlaştırılmış artıklarını x ekseninde görüntüleyen bir dağılım grafiği oluşturabilirsiniz. y.
Dağılım grafiğindeki noktalar bir trend sergiliyorsa, değişen varyans mevcut demektir.
Aşağıdaki grafik, heteroskedastisitenin sorun olmadığı bir regresyon modeli örneğini göstermektedir:
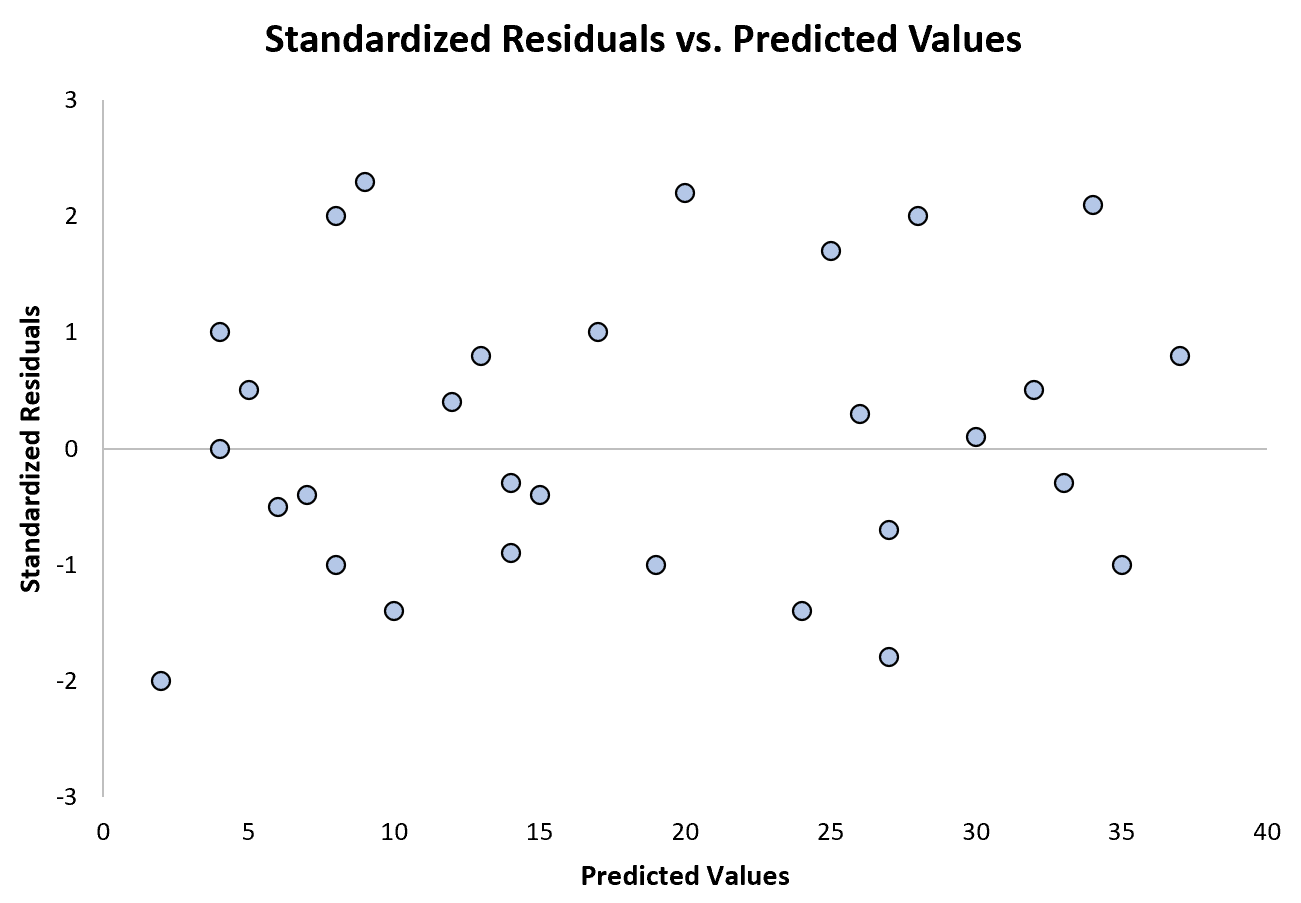
Standartlaştırılmış artıkların net bir model olmadan sıfır etrafında dağıldığını unutmayın.
Aşağıdaki grafik, değişen varyansın bir sorun olduğu bir regresyon modeli örneğini göstermektedir:
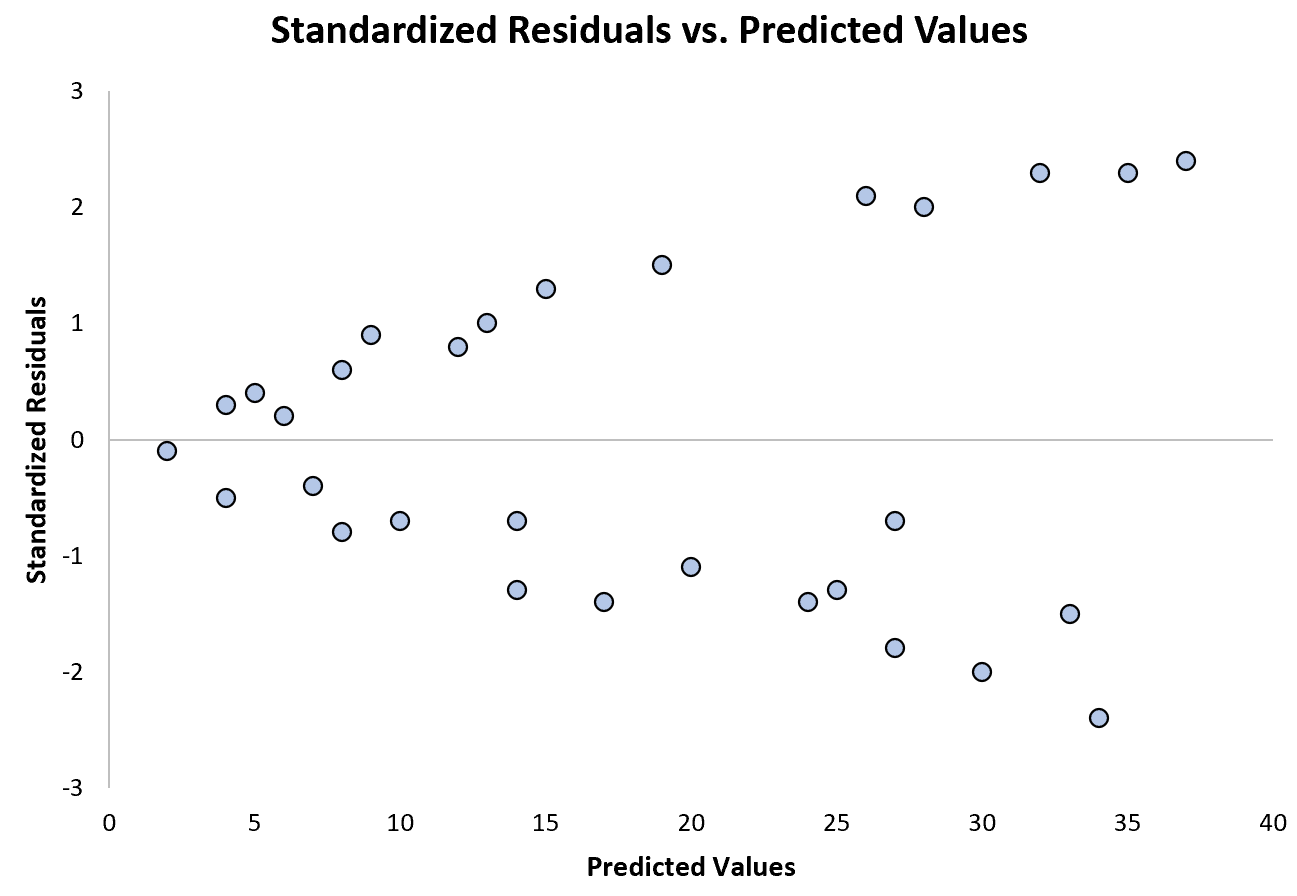
Tahmin edilen değerler arttıkça standartlaştırılmış artıkların nasıl daha fazla yayıldığına dikkat edin. Bu “koni” şekli değişen varyansın klasik bir işaretidir:
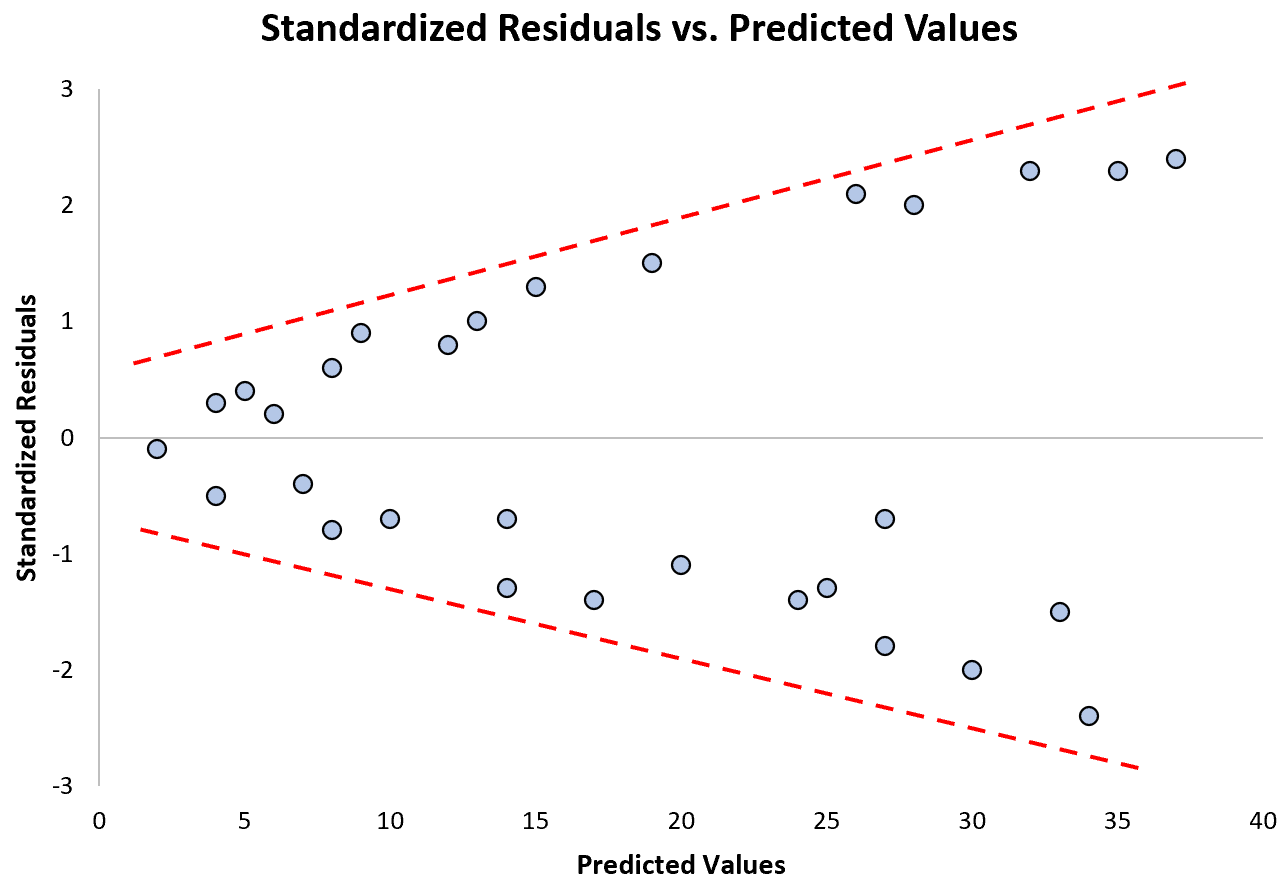
Bu varsayıma uyulmazsa ne yapılmalı?
Heteroskedasticity’yi düzeltmenin üç yaygın yolu vardır:
1. Yanıt değişkenini dönüştürün. Heteroskedasticity ile başa çıkmanın en yaygın yolu, yanıt değişkeninin tüm değerlerinin logunu, karekökünü veya küp kökünü alarak yanıt değişkenini dönüştürmektir. Bu genellikle heteroskedastisitenin ortadan kalkmasıyla sonuçlanır.
2. Yanıt değişkenini yeniden tanımlayın. Yanıt değişkenini yeniden tanımlamanın bir yolu, ham değer yerine bir oran kullanmaktır. Örneğin, bir şehirdeki çiçekçi sayısını tahmin etmek için nüfus büyüklüğünü kullanmak yerine, kişi başına düşen çiçekçi sayısını tahmin etmek için nüfus büyüklüğünü kullanabiliriz.
Çoğu durumda bu, çiçekçilerin sayısından ziyade kişi başına düşen çiçekçilerin sayısını ölçtüğümüz için daha büyük popülasyonlarda doğal olarak oluşan değişkenliği azaltır.
3. Ağırlıklı regresyon kullanın. Değişen varyanslılığı düzeltmenin başka bir yolu, her veri noktasına, uydurulmuş değerinin varyansına dayalı olarak bir ağırlık atayan ağırlıklı regresyon kullanmaktır.
Temel olarak bu, daha yüksek varyansa sahip veri noktalarına düşük ağırlık vererek bunların kalan karelerini azaltır. Uygun ağırlıklar kullanıldığında değişen varyans sorunu ortadan kaldırılabilir.
İlgili : R’de Ağırlıklı Regresyon Nasıl Gerçekleştirilir
Varsayım 4: Çok değişkenli normallik
Çoklu doğrusal regresyon, model artıklarının normal şekilde dağıldığını varsayar.
Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir
Bu varsayımın karşılanıp karşılanmadığını kontrol etmenin iki yaygın yolu vardır:
1. QQ grafiklerini kullanarak hipotezi görsel olarak doğrulayın .
Kantil-kantil grafiğinin kısaltması olan QQ grafiği, bir modelin artıklarının normal dağılıma uyup uymadığını belirlemek için kullanabileceğimiz bir grafik türüdür. Grafikteki noktalar kabaca düz bir çapraz çizgi oluşturuyorsa normallik varsayımı karşılanmıştır.
Aşağıdaki QQ grafiği kabaca normal dağılıma uyan bir kalıntı örneğini göstermektedir:
Bununla birlikte, aşağıdaki QQ grafiği, artıkların düz bir çapraz çizgiden açıkça saptığı ve normal dağılıma uymadıklarını gösteren bir durumun örneğini göstermektedir:
2. Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre veya D’Agostino-Pearson gibi resmi bir istatistiksel test kullanarak hipotezi doğrulayın.
Bu testlerin büyük numune boyutlarına duyarlı olduğunu unutmayın; yani, numune boyutunuz çok büyük olduğunda genellikle artıkların normal olmadığı sonucuna varırlar. Bu hipotezi doğrulamak için QQ grafiği gibi grafiksel yöntemleri kullanmanın genellikle daha kolay olmasının nedeni budur.
Bu varsayıma uyulmazsa ne yapılmalı?
Normallik varsayımı karşılanmazsa birkaç seçeneğiniz vardır:
1. Öncelikle verilerde normallik varsayımının ihlaline yol açacak aşırı uç değerlerin mevcut olup olmadığını kontrol edin.
2. Daha sonra yanıt değişkenine, örneğin yanıt değişkeninin tüm değerlerinin karekökünü, logunu veya küp kökünü alarak doğrusal olmayan bir dönüşüm uygulayabilirsiniz. Bu genellikle model artıklarının daha normal bir dağılımıyla sonuçlanır.
Ek kaynaklar
Aşağıdaki eğitimler çoklu doğrusal regresyon ve varsayımları hakkında ek bilgi sağlar:
Çoklu Doğrusal Regresyona Giriş
Regresyon Analizinde Değişken Varyans Kılavuzu
Regresyonda Çoklu Bağlantı ve VIF Kılavuzu
Aşağıdaki eğitimlerde, farklı istatistiksel yazılımlar kullanılarak çoklu doğrusal regresyonun nasıl gerçekleştirileceğine ilişkin adım adım örnekler verilmektedir:
Excel’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
SPSS’de çoklu doğrusal regresyon nasıl gerçekleştirilir
Stata’da çoklu doğrusal regresyon nasıl gerçekleştirilir
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil