Dağılım grafiği

Bu makalede dağılım grafiklerinin ne olduğu açıklanmaktadır. Böylelikle nokta bulutunun ne için kullanıldığını, nokta bulutunun nasıl oluşturulacağını, nasıl yorumlanacağını ve nokta bulutu örneklerini keşfedeceksiniz.

Nokta bulutu nedir?

Dağılım grafiği veya dağılım grafiği , iki değişkenden oluşan bir veri kümesinin iki Kartezyen koordinat ekseninde grafiklendiği bir tür istatistiksel diyagramdır.

Bu nedenle, iki istatistiksel değişken arasındaki ilişkiyi analiz etmek için dağılım grafikleri kullanılır.

Dağılım grafiklerinin korelasyon diyagramı veya dağılım grafiği gibi birkaç farklı adı vardır.

Dağılım diyagramının tıpkı Pareto şeması, neden-sonuç diyagramı, akış şeması vb. gibi kalite kontrolün temel araçlarından biri olarak kabul edildiğini belirtmek gerekir.

Dağılım grafiği nasıl yapılır

Bir dağılım grafiği oluşturmak için aşağıdaki adımları izlemeniz gerekir:

1. Analiz etmek istediğiniz örnekten istatistiksel verileri toplayın. Bir dağılım grafiği oluşturmak için en az iki niceliksel değişkenin olması gerektiğini unutmayın.
2. Dağılım grafiğinin iki eksenini çizin.
3. Grafiği çizilecek iki istatistiksel değişkeni belirleyin.
4. Grafiğin her ekseninin ölçeğini kalibre edin. Bunu yapmak için öncelikle her değişkenin minimum ve maksimumunu bulmanız ve bu değerlere göre her ekseni ölçeklendirmeniz önerilir.
5. Dağılım grafiğindeki her veri çiftini bir noktayla temsil edin.
6. Elde edilen dağılım diyagramını analiz edin ve yorumlayın.

Dağılım grafiği örneği

Dağılım diyagramının tanımını ve oluşumuna ilişkin teoriyi gördükten sonra, bu bölümde örnek olarak bu türden bir diyagram sunulmaktadır.

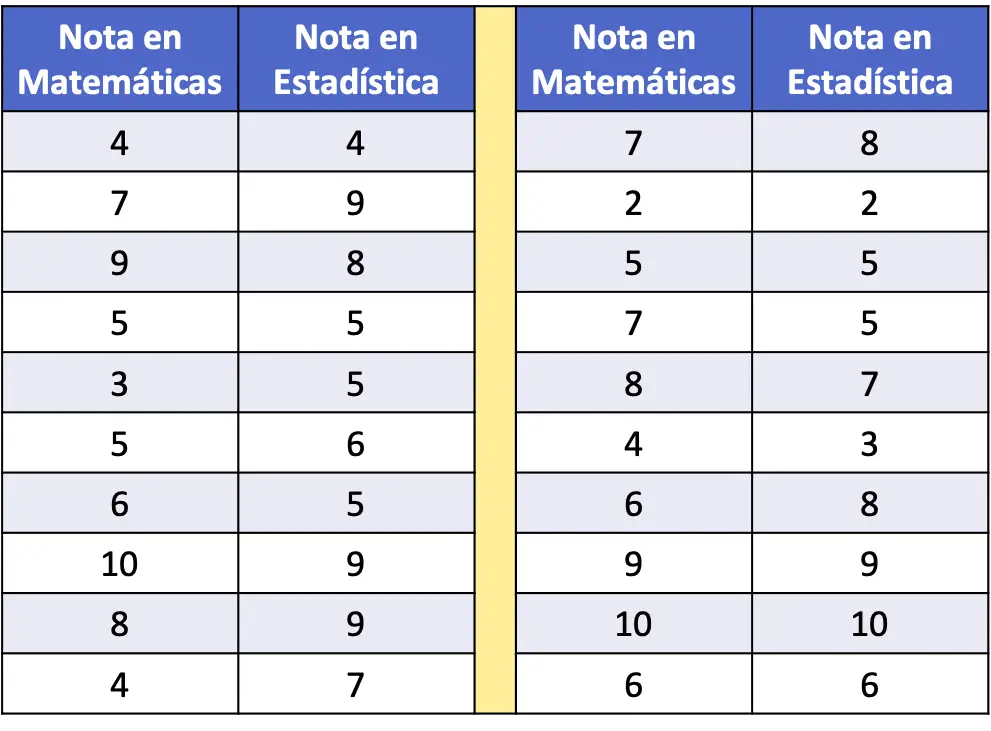
• Aşağıdaki frekans tablosunda 20 kişilik bir örneklemin matematik ve istatistik puanları veri olarak toplanmıştır. Veri kümesini bir dağılım grafiğine çizin ve analiz edin.

Veri serisini bir dağılım grafiğinde temsil etmek için, iki ekseni çizmemiz, bunları kalibre etmemiz ve her veri çifti için grafik üzerinde bir nokta çizmemiz yeterlidir. Grafikteki bir noktanın, değerlerinin her birine karşılık gelen hayali çizgilerin kesişim noktasına yerleştirildiğini unutmayın.

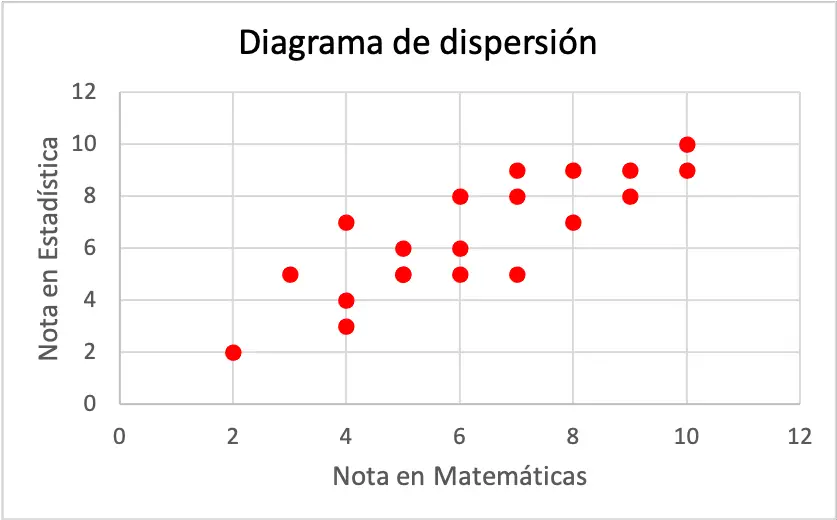
Dağılım grafiğinin her ekseni bir değişkeni temsil eder. Daha doğrusu yatay eksen matematikte alınan nota, dikey eksen ise istatistikte alınan nota karşılık gelir.

Dağılım grafiğinden görebileceğiniz gibi, iki değişken arasında pozitif bir korelasyon var çünkü bir değişken artarken diğer değişken de artıyor. Dolayısıyla bir öğrencinin matematikte daha iyi not alması durumunda istatistikte de daha iyi not alması ihtimalinin daha yüksek olduğu ve bunun tersinin de geçerli olduğu sonucuna varılmıştır.

Ancak önceki sonuç, bir değişkenin diğerinin nedeni olduğu anlamına gelmez, çünkü matematikte iyi bir not almak, hiçbir şey yapmadan istatistikte otomatik olarak iyi bir not almayı garanti etmez; bunun yerine kişi her iki konuyu da çalışmalıdır. Bir sonraki bölümde bu kavram hakkında daha detaylı bilgi vereceğiz.

Dağılım grafiği ve korelasyon

Bir dağılım diyagramından iki değişken arasındaki korelasyonun türünü belirlemek mümkündür:

• Doğrudan korelasyon (veya pozitif korelasyon) : Bir değişken arttığında diğeri de artar.
• Ters korelasyon (veya negatif korelasyon) : Bir değişken arttığında diğeri azalır ve bunun tersi de geçerlidir; bir değişken azaldığında diğeri artar.
• Sıfır korelasyon (Korelasyon yok) : İki değişken arasında herhangi bir ilişki yoktur.

Benzer şekilde, iki değişken arasındaki korelasyonun doğrudan ya da ters olmasına bakılmaksızın, korelasyon, iki değişken arasındaki ilişkinin güçlü ya da zayıf olmasına göre de sınıflandırılabilir.

• Güçlü korelasyon: İki değişken yakından bağlantılıdır. Noktalar nokta bulutu üzerinde bir araya getirilir. Bu, değişkenler arasındaki ilişkinin tanımlanmasını kolaylaştırır.
• Düşük korelasyon : İki değişken arasında bir ilişki vardır ancak tanımlanması zordur. Nokta bulutunda noktalar birbirinden uzaktadır.

Öte yandan korelasyon, bir formül kullanılarak sayısal olarak da hesaplanabilir; bu, iki farklı değişkenin ne kadar yakından ilişkili olduğunu matematiksel olarak bilmenizi sağlar. Nasıl çalıştığını görmek için aşağıdaki bağlantıya tıklayın:

Unutmayın ki iki değişken arasında korelasyon olsa bile bu, aralarında nedensellik olduğu anlamına gelmez; yani iki değişken arasındaki korelasyon, bir değişkendeki değişimin diğerindeki değişimin nedeni olduğu anlamına gelmez. değişken.

Yani, önceki bölümdeki dağılım grafiği gibi, matematik notu ile istatistik notu arasında pozitif bir korelasyon olmasına rağmen, matematikte iyi bir not almak, istatistikte de iyi bir not almak anlamına gelmez, çünkü sadece matematik çalışırsanız kesinlikle başarısız olursunuz. istatistiklerde. Dolayısıyla iki değişken birbiriyle ilişkilidir ancak sebep ve sonuç değildir.

Daha fazlasını öğrenmek için aşağıdaki yazıya devam edebilirsiniz:

Nokta bulutunun avantajları ve dezavantajları

Dağılım grafiğinin özelliklerinden dolayı bu tür istatistiksel grafiğin avantajları ve dezavantajları vardır.

Avantajı:

• Bir dizi veriyi dağılım grafiğinde temsil etmek oldukça basittir.
• Dağılım grafiği, iki değişken arasındaki ilişkiyi görsel olarak analiz etmenize olanak tanıyarak sonuç çıkarmayı kolaylaştırır.
• Dağılım grafikleri aynı zamanda derinlemesine bir istatistiksel çalışmada ön veri araştırması olarak da kullanılabilir.

Dezavantajları:

• Bu tür diyagramlar niteliksel değişkenleri temsil etmede kullanışlı değildir.
• Bir dağılım grafiğini yorumlamak, iki değişken arasında hatalı neden-sonuç sonucuna varılmasına yol açabilir.
• Dağılım grafikleri ikiden fazla değişken arasındaki ilişkiyi analiz etmenize izin vermez.