Dağıtım işlevi

İle Dr.benjamin anderson Ağustos 5, 2023 Olasılık 0 Yorum

Bu yazıda dağıtım fonksiyonunun açıklamasını, değerlerinin nasıl hesaplandığını ve dağıtım fonksiyonunun gerçek dünyadan bir örneğini bulacaksınız. Ayrıca dağılım fonksiyonu ile yoğunluk fonksiyonu arasındaki farkları da görebileceksiniz.

Dağıtım fonksiyonu nedir?

Kümülatif dağılım fonksiyonu olarak da adlandırılan dağılım fonksiyonu , bir dağılımın kümülatif olasılığını gösteren matematiksel bir fonksiyondur. Yani herhangi bir değere ait dağılım fonksiyonunun görüntüsü, değişkenin o değeri veya daha düşük bir değeri alma olasılığına eşittir.

Kümülatif dağıtım fonksiyonu, genel sembolü büyük F olmasına rağmen FDA kısaltmasıyla da anılabilir.

Bu nedenle dağıtım fonksiyonu aşağıdaki formülle tanımlanır:

$F(x)=P[X\leq x]$

Dağıtım fonksiyonu nasıl hesaplanır

Daha sonra olasılık dağılımının kesikli veya sürekli olmasına bağlı olarak dağılım fonksiyonunun değerinin nasıl hesaplanacağını açıklıyoruz.

Gizli kutu

Rastgele değişken ayrık ise, kümülatif dağılım fonksiyonu x’e eşit veya ondan küçük tüm değerlerin olasılıklarının toplamına eşittir.

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

Altın

$f(u)$

ayrık değişkenle ilişkili olasılık fonksiyonudur.

Devam eden dava

Rastgele değişken sürekli ise, kümülatif dağılım fonksiyonu yoğunluk fonksiyonunun eksi sonsuzdan söz konusu değere kadar olan integraline eşdeğerdir.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

Altın

$f(u)$

sürekli değişkenle ilişkili yoğunluk fonksiyonudur.

Dağıtım Fonksiyonu Örneği

Artık dağıtım fonksiyonunun tanımını bildiğimize göre, bir dağıtım fonksiyonu değerinin nasıl hesaplanacağını öğrenmek için adım adım pratik bir örneğe bakalım.

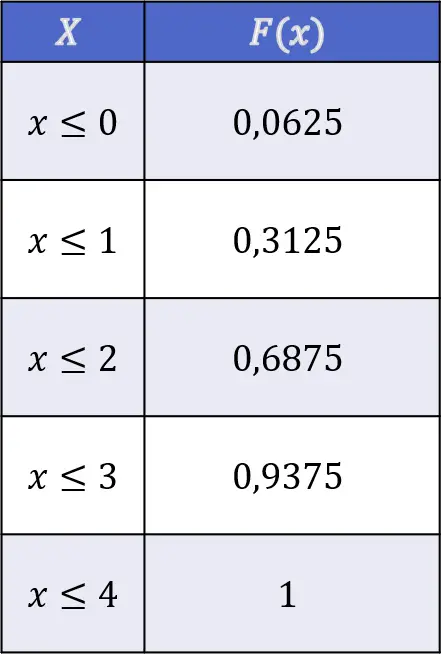
Bir madeni paranın dört kez atılmasıyla ilgili rastgele deney için dağılım fonksiyonunu hesaplayın.

Alıştırmayı çözmek için öncelikle dört yazı-tura atışı sırasında elde edilen tura sayısıyla ilgili tüm olasılıkları hesaplamanız gerekir:

dört madeni parayı havaya atma olasılığı

Dolayısıyla kesikli bir değişken olduğundan dağılım fonksiyonunun görüntülerini belirlemek için söz konusu değişkenin değerine kadar olasılıkları toplamak yeterlidir:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

Böylece dört bağımsız paranın atılmasıyla tura atılmasının dağılım fonksiyonunun değerleri aşağıdaki gibidir:

Dağıtım fonksiyonunun özellikleri

Değişkenin türünden bağımsız olarak dağıtım fonksiyonu her zaman aşağıdaki özelliklere sahiptir:

Kümülatif dağılım fonksiyonunun değeri 0 ile 1 dahil arasındadır.

$0\leq F(x) \leq 1$

X sonsuza giderken bir dağılım fonksiyonunun limiti 1’e eşittir.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

Öte yandan, x eksi sonsuza yaklaşırken bir dağılım fonksiyonunun limiti sıfırdır.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

Özellikleri gereği dağılım fonksiyonu monotondur ve azalmaz.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

Ayrıca, eğer
$a\leq b$

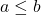
aşağıdaki denklemler sağlanır.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Dağıtım fonksiyonu ve yoğunluk fonksiyonu

Son olarak, bu iki istatistiksel kavram sıklıkla karıştırıldığı için dağılım fonksiyonu ile yoğunluk fonksiyonu arasındaki farkın ne olduğunu göreceğiz.

Dağılım fonksiyonu ile yoğunluk fonksiyonu arasındaki fark, tanımladıkları olasılık türüdür. Yoğunluk fonksiyonu değişkenin belirli bir değer alma olasılığını, dağılım fonksiyonu ise değişkenin kümülatif olasılığını açıklar.

Yani değişkenin belirli bir değere eşit veya daha küçük olma olasılığını hesaplamak için dağılım fonksiyonu kullanılır.

Yoğunluk fonksiyonunun yalnızca sürekli değişkenlere atıfta bulunduğunu, dolayısıyla bu ayrımın yalnızca üzerinde çalışılan değişkenin sürekli olması durumunda anlamlı olduğunu unutmayın.

Ortalaması 1 ve standart sapması 0,5 olan normal bir dağılım izleyen bir değişkenin yoğunluk fonksiyonuyla karşılaştırıldığında dağılım fonksiyonunun grafiksel gösteriminin nasıl değiştiğine dikkat edin:

dağıtım fonksiyonu ile yoğunluk fonksiyonu arasındaki fark

Yoğunluk işlevi hakkında daha fazla bilgi edinmek için aşağıdaki makaleye bakın:

➤ Bakınız: yoğunluk fonksiyonu

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil