Anova varsayımları nasıl kontrol edilir

Tek yönlü ANOVA, üç veya daha fazla bağımsız grubun ortalamaları arasında anlamlı bir fark olup olmadığını belirlemek için kullanılan istatistiksel bir testtir.

Tek yönlü ANOVA’yı ne zaman kullanabileceğimize bir örnek:

90 kişilik bir sınıfı rastgele 30 kişilik üç gruba ayırıyorsunuz. Her grup bir sınava hazırlanmak için bir ay boyunca farklı bir çalışma tekniği kullanıyor. Ay sonunda tüm öğrenciler aynı sınava girerler.

Çalışma tekniğinin sınav puanları üzerinde etkisi olup olmadığını bilmek istiyorsunuz. Yani üç grubun ortalama puanları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü bir ANOVA gerçekleştirirsiniz.

Tek yönlü ANOVA yapmadan önce üç varsayımın karşılandığını doğrulamamız gerekir.

1. Normallik – Her örnek normal dağılmış bir popülasyondan alınmıştır.

2. Eşit varyanslar – Örneklerin alındığı popülasyonların varyansları eşittir.

3. Bağımsızlık – Her grup içindeki gözlemler birbirinden bağımsızdır ve gruplar içindeki gözlemler rastgele örnekleme yoluyla elde edilmiştir.

Bu varsayımlar karşılanmazsa tek yönlü ANOVA’mızın sonuçları güvenilir olmayabilir.

Bu yazıda bu varsayımların nasıl kontrol edileceğini ve bunlardan herhangi birinin ihlal edilmesi durumunda ne yapılacağını açıklıyoruz.

Varsayım #1: normallik

ANOVA, her örneğin normal dağılmış bir popülasyondan alındığını varsayar.

R’de bu hipotez nasıl kontrol edilir:

Bu hipotezi doğrulamak için iki yaklaşım kullanabiliriz:

• Histogramları veya QQ grafiklerini kullanarak hipotezi görsel olarak doğrulayın.
• Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre veya D’Agostino-Pearson gibi resmi istatistiksel testleri kullanarak hipotezi doğrulayın.

Örneğin, bir kilo verme deneyine katılmak üzere 90 kişiyi işe aldığımızı ve 30 kişiyi bir ay boyunca Program A, Program B veya Program C’yi takip etmek üzere rastgele atadığımızı varsayalım. Programın kilo kaybı üzerinde bir etkisi olup olmadığını görmek için tek yönlü bir ANOVA yapmak istiyoruz. Aşağıdaki kod, histogramlar, QQ grafikleri ve Shapiro-Wilk testi kullanılarak normallik varsayımının nasıl kontrol edileceğini gösterir.

1. ANOVA modelini takın.

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. Yanıt değerlerinin histogramını oluşturun.

 #create histogram
hist(data$weight_loss)

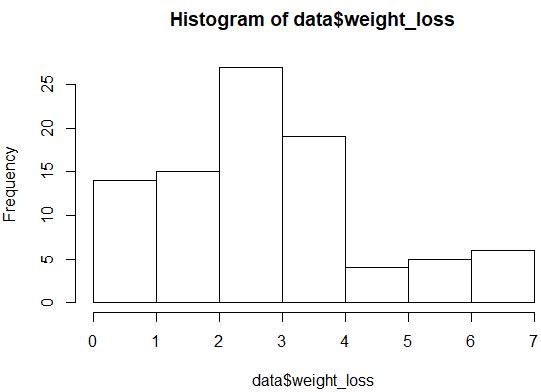
Dağılım çok normal bir dağılıma sahip görünmüyor (örneğin “çan” şeklinde değil), ancak dağılıma yeniden bakmak için bir QQ grafiği de oluşturabiliriz.

3. Artıkların QQ grafiğini oluşturun

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

Genel olarak, eğer veri noktaları bir QQ grafiğinde düz bir çapraz çizgi boyunca yer alıyorsa, o zaman veri seti muhtemelen normal bir dağılım izliyor demektir. Bu durumda, uçlar boyunca çizgiden gözle görülür bir sapma olduğunu görebiliriz, bu da verilerin normal şekilde dağılmadığını gösterebilir.

4. Normallik için Shapiro-Wilk testini gerçekleştirin.

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

Shapiro-Wilk testi, örneklerin normal dağılımdan geldiği şeklindeki sıfır hipotezini, örneklerin normal dağılımdan gelmediği şeklindeki alternatif hipoteze karşı test eder. Bu durumda testin p değeri 0,005999 olup alfa düzeyi olan 0,05’ten düşüktür. Bu durum örneklerin normal dağılıma uymadığını göstermektedir.

Bu varsayıma uyulmazsa ne yapılmalı:

Genel olarak tek yönlü bir ANOVA, örneklem boyutları yeterince büyük olduğu sürece normallik varsayımının ihlallerine karşı oldukça sağlam kabul edilir.

Ek olarak, çok büyük örnekleriniz varsa Shapiro-Wilk testi gibi istatistiksel testler neredeyse her zaman verilerinizin normal olmadığını söyleyecektir. Bu nedenle, histogramlar ve QQ grafikleri gibi grafikleri kullanarak verilerinizi görsel olarak incelemek genellikle en iyisidir. Sadece grafiklere bakarak verilerin normal dağılıp dağılmadığına dair oldukça iyi bir fikir edinebilirsiniz.

Normallik varsayımı ciddi şekilde ihlal edilmişse veya sadece çok muhafazakar olmak istiyorsanız iki seçeneğiniz vardır:

(1) Dağılımların daha normal dağılması için verilerinizin yanıt değerlerini dönüştürün.

(2) Normallik varsayımını gerektirmeyen Kruskal-Wallis testi gibi eşdeğer bir parametrik olmayan test gerçekleştirin.

Varsayım #2: eşit varyans

ANOVA, örneklerin alındığı popülasyonların varyanslarının eşit olduğunu varsayar.

R’de bu hipotez nasıl kontrol edilir:

Bu hipotezi R’de iki yaklaşım kullanarak doğrulayabiliriz:

• Kutu grafiklerini kullanarak hipotezi görsel olarak doğrulayın.
• Bartlett testi gibi resmi istatistiksel testleri kullanarak hipotezi test edin.

Aşağıdaki kod, daha önce oluşturduğumuz sahte kilo verme veri kümesini kullanarak bunun nasıl yapılacağını göstermektedir.

1. Kutu grafikleri oluşturun.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

Her gruptaki kilo kaybındaki farklılık, her kutu grafiğinin uzunluğuna göre gözlemlenebilir. Kutu ne kadar uzun olursa varyans da o kadar yüksek olur. Örneğin Program A ve Program B ile karşılaştırıldığında Program C katılımcıları için varyansın biraz daha yüksek olduğunu görebiliriz.

2. Bartlett testini gerçekleştirin.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

Bartlett testi, örneklerin eşit varyansa sahip olduğunu ifade eden boş hipotezi, örneklerin eşit varyansa sahip olmadığı alternatif hipotezine karşı test eder. Bu durumda testin p değeri 0,01599 olup alfa düzeyi olan 0,05’ten düşüktür. Bu durum örneklerin hepsinin aynı varyansa sahip olmadığını göstermektedir.

Bu varsayıma uyulmazsa ne yapılmalı:

Genel olarak, tek yönlü bir ANOVA, her grup aynı örneklem büyüklüğüne sahip olduğu sürece eşit varyans varsayımının ihlallerine karşı oldukça sağlam kabul edilir.

Ancak örneklem büyüklükleri aynı değilse ve bu varsayım ciddi şekilde ihlal ediliyorsa bunun yerine tek yönlü ANOVA’nın parametrik olmayan versiyonu olan Kruskal-Wallis testini çalıştırabilirsiniz.

Varsayım #3: Bağımsızlık

ANOVA şunu varsayar:

• Her grubun gözlemleri diğer tüm grupların gözlemlerinden bağımsızdır.
• Her gruptaki gözlemler rastgele bir örnekle elde edildi.

Bu hipotez nasıl doğrulanır:

Her gruptaki gözlemlerin bağımsız olduğunu ve bunların rastgele bir örnekle elde edildiğini doğrulamak için kullanabileceğiniz resmi bir test yoktur. Bu varsayımı karşılamanın tek yolu rastgele bir tasarım kullanmaktır.

Bu varsayıma uyulmazsa ne yapılmalı:

Ne yazık ki bu varsayım karşılanmazsa yapabileceğiniz pek bir şey yok. Basitçe söylemek gerekirse, veriler her gruptaki gözlemlerin diğer gruplardaki gözlemlerden bağımsız olmayacak şekilde toplanmışsa veya her gruptaki gözlemler rastgele bir süreçle elde edilmemişse ANOVA sonuçları güvenilir olmayacaktır. .

Bu varsayım karşılanmazsa yapılacak en iyi şey, deneyi rastgele bir tasarım kullanarak yeniden oluşturmaktır.

Daha fazla okuma:

R’de tek yönlü ANOVA nasıl gerçekleştirilir
Excel’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir