Google e-tablolar'da doğrusal regresyon nasıl gerçekleştirilir?

Doğrusal regresyon, bir veya daha fazla açıklayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanılabilen bir yöntemdir.

Yalnızca bir açıklayıcı değişken olduğunda basit doğrusal regresyon, iki veya daha fazla açıklayıcı değişken olduğunda çoklu doğrusal regresyon kullanırız.

Her iki regresyon türü de aşağıdaki sözdizimini kullanan Google E-Tablolar LINEST() işlevi kullanılarak gerçekleştirilebilir:

DOT (bilinen_veriler_y, bilinen_veriler_x, hesapla_b, ayrıntılı)

Altın:

• bilinen_data_y: yanıt değerleri dizisi
• bilinen_data_x: Açıklayıcı değerler tablosu
• hesapla_b: kesmenin hesaplanıp hesaplanmayacağını belirtir. Bu, varsayılan olarak DOĞRU’dur ve doğrusal regresyon için bunu bu şekilde bırakıyoruz.
• ayrıntılı: Yalnızca eğim ve kesişme noktasının ötesinde ek regresyon istatistikleri sağlanıp sağlanmayacağını belirtir. Bu varsayılan olarak YANLIŞ’tır ancak örneklerimizde bunun DOĞRU olduğunu belirteceğiz.

Aşağıdaki örnekler bu fonksiyonun pratikte nasıl kullanılacağını göstermektedir.

Google E-Tablolar’da basit doğrusal regresyon

Çalışılan saatlerle sınav sonuçları arasındaki ilişkiyi anlamak istediğimizi varsayalım. Sınava çalışmak ve sınavda alınan not.

Bu ilişkiyi araştırmak için, açıklayıcı değişken olarak çalışılan saatleri ve yanıt değişkeni olarak sınav puanlarını kullanarak basit bir doğrusal regresyon gerçekleştirebiliriz.

Aşağıdaki ekran görüntüsü, D2 hücresinde kullanılan aşağıdaki formülle 20 öğrenciden oluşan bir veri kümesini kullanarak basit bir doğrusal regresyonun nasıl gerçekleştirileceğini gösterir:

= SATIR ( B2:B21 , A2:A21 , DOĞRU , DOĞRU )

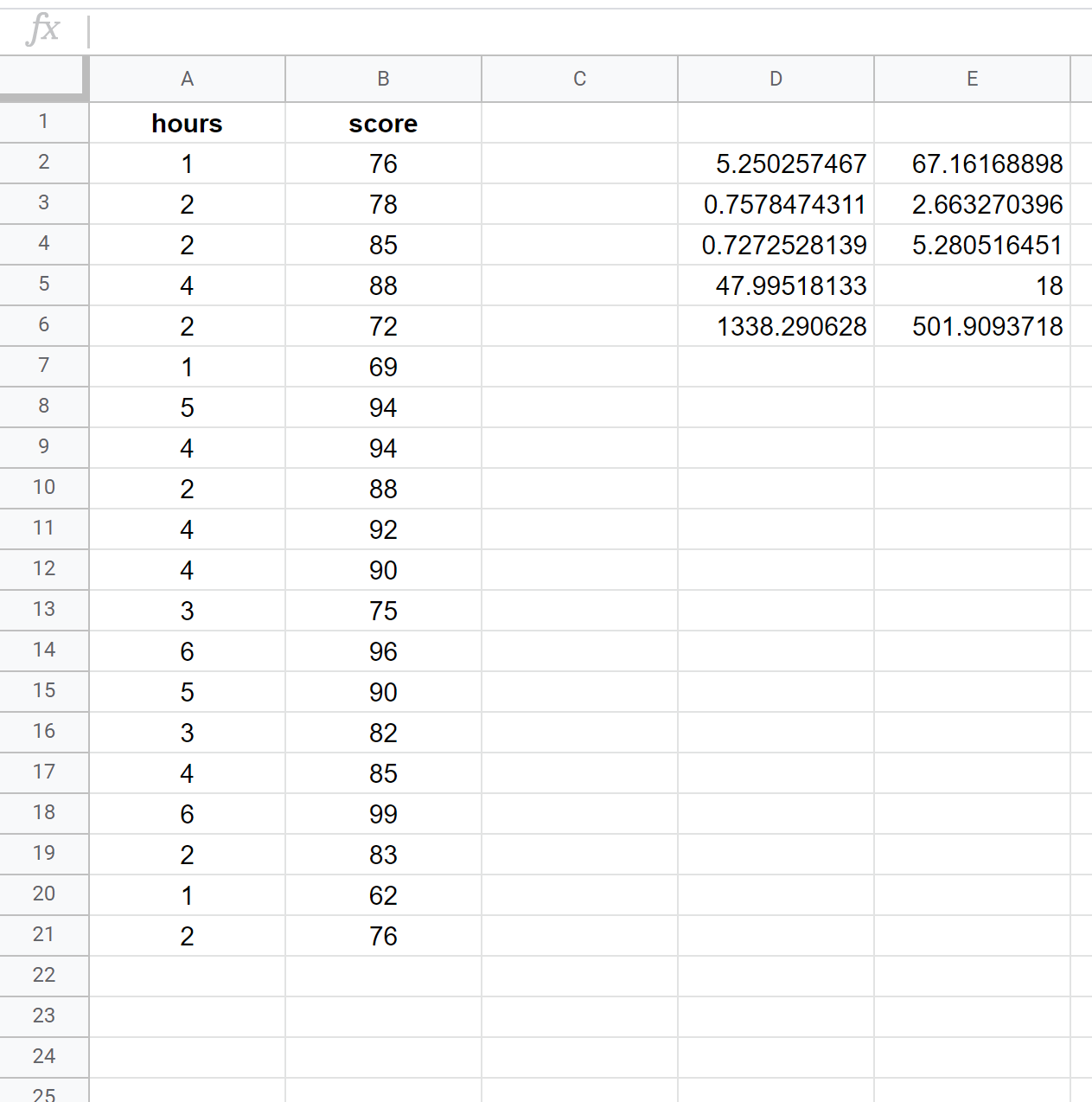
Aşağıdaki ekran görüntüsü çıktı için ek açıklamalar sağlar:

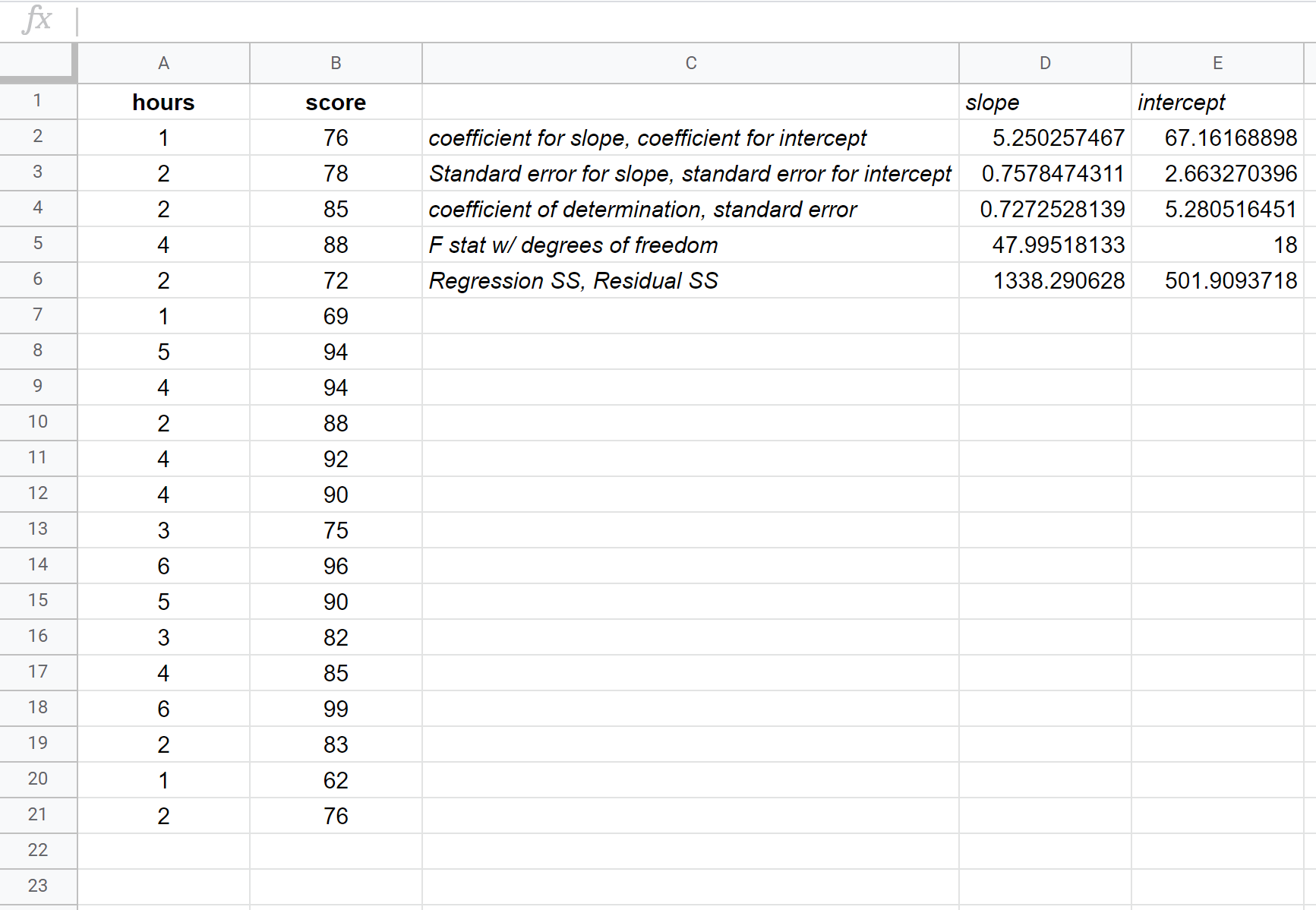
Sonuçtaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

R Kare: 0,72725 . Buna belirleme katsayısı denir. Açıklayıcı değişken tarafından açıklanabilen, yanıt değişkenindeki varyansın oranıdır. Bu örnekte sınav puanlarındaki değişimin yaklaşık %72,73’ü çalışılan saat sayısıyla açıklanabilir.

Standart hata: 5.2805 . Bu, gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu örnekte gözlemlenen değerler regresyon doğrusundan ortalama 5,2805 birim sapmaktadır.

Katsayılar: Katsayılar bize tahmini regresyon denklemini yazmak için gereken sayıları verir. Bu örnekte tahmini regresyon denklemi şöyledir:

Sınav puanı = 67,16 + 5,2503*(saat)

Saat katsayısını, çalışılan her ek saat için sınav puanının ortalama 5,2503 artması gerektiği şeklinde yorumluyoruz. Kesişme katsayısını, sıfır saat okuyan bir öğrenci için beklenen sınav puanının 67,16 olduğu şeklinde yorumluyoruz.

Bu tahmini regresyon denklemini, çalışma saati sayısına bağlı olarak bir öğrencinin beklenen sınav puanını hesaplamak için kullanabiliriz. Örneğin üç saat ders çalışan bir öğrencinin sınav puanının 82,91 olması gerekir:

Sınav puanı = 67,16 + 5,2503*(3) = 82,91

Google E-Tablolarda Çoklu Doğrusal Regresyon

Diyelim ki, ders çalışmak için harcanan saatlerin ve alınan hazırlık sınavlarının sayısının, bir öğrencinin belirli bir üniversiteye giriş sınavından aldığı notu etkileyip etkilemediğini bilmek istiyoruz.

Bu ilişkiyi araştırmak için çalışılan saatleri ve alınan hazırlık sınavlarını açıklayıcı değişkenler olarak ve sınav sonuçlarını yanıt değişkeni olarak kullanarak çoklu doğrusal regresyon gerçekleştirebiliriz.

Aşağıdaki ekran görüntüsü, E2 hücresinde kullanılan aşağıdaki formülle 20 öğrenciden oluşan bir veri kümesini kullanarak çoklu doğrusal regresyonun nasıl gerçekleştirileceğini gösterir:

= SAĞ ( C2:C21 , A2:B21 , DOĞRU , DOĞRU )

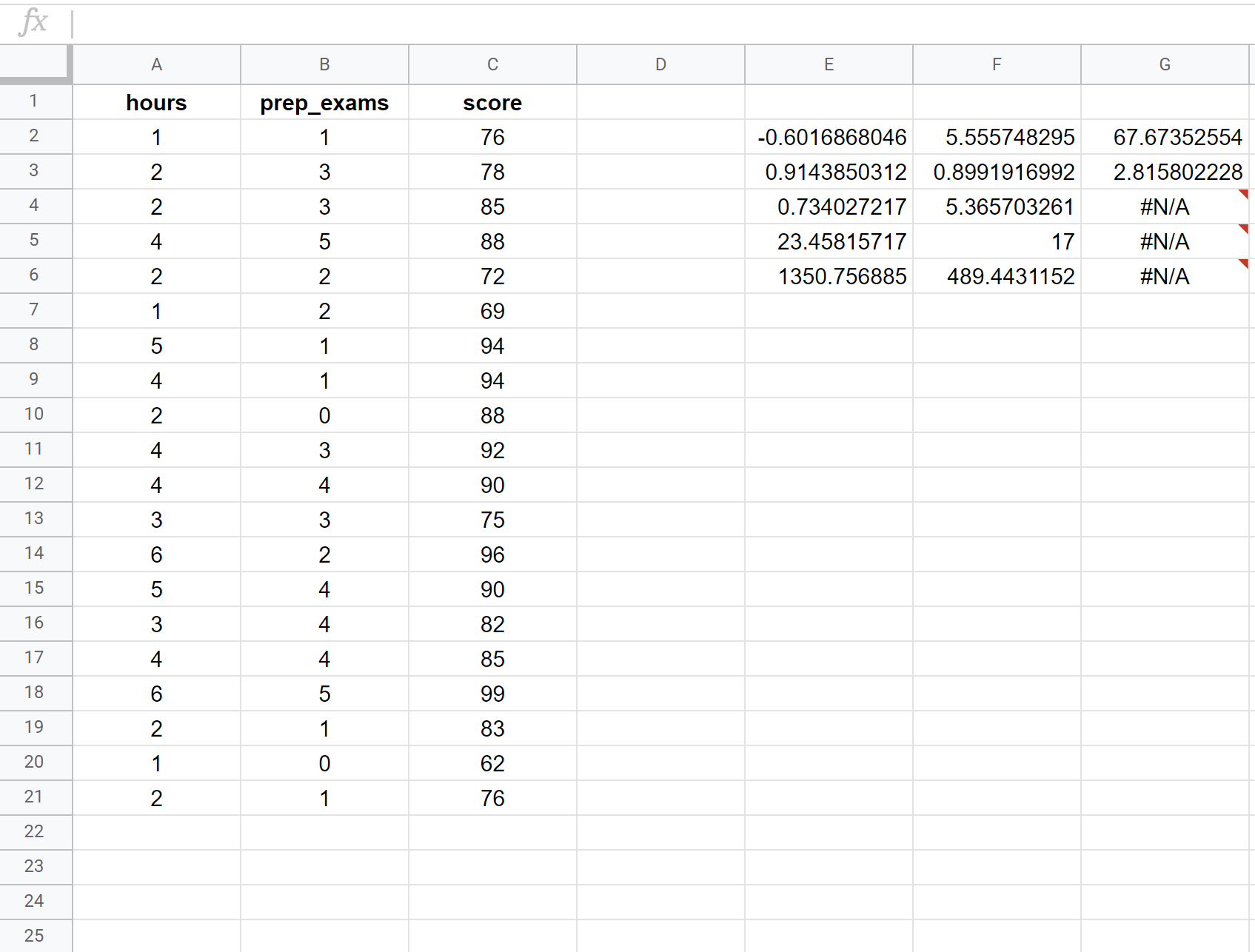
Sonuçtaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

R Kare: 0,734 . Buna belirleme katsayısı denir. Açıklayıcı değişkenler tarafından açıklanabilen yanıt değişkeninin varyansının oranıdır. Bu örnekte sınav puanlarındaki farklılığın %73,4’ü çalışılan saat ve girilen hazırlık sınavı sayısıyla açıklanmaktadır.

Standart hata: 5,3657 . Bu, gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu örnekte gözlemlenen değerler regresyon doğrusundan ortalama 5,3657 birim sapmaktadır.

Tahmini regresyon denklemi: Aşağıdaki tahmini regresyon denklemini oluşturmak için model çıktısındaki katsayıları kullanabiliriz:

Sınav puanı = 67,67 + 5,56*(saat) – 0,60*(hazırlık sınavları)

Bu tahmini regresyon denklemini, bir öğrencinin çalışma saati ve girdiği deneme sınavlarının sayısına bağlı olarak beklenen sınav puanını hesaplamak için kullanabiliriz. Örneğin üç saat çalışıp hazırlık sınavına giren bir öğrencinin notunun 83,75 olması gerekir:

Sınav puanı = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Ek kaynaklar

Aşağıdaki eğitimlerde Google E-Tablolar’da diğer yaygın görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

Google E-Tablolarda polinom regresyonu nasıl gerçekleştirilir?
Google E-Tablolarda Artık Grafik Nasıl Oluşturulur