Doğrusal regresyonun dört varsayımı

Doğrusal regresyon , iki değişken (x ve y) arasındaki ilişkiyi anlamak için kullanabileceğimiz yararlı bir istatistiksel yöntemdir. Ancak doğrusal regresyon gerçekleştirmeden önce dört varsayımın karşılandığından emin olmalıyız:

1. Doğrusal ilişki: Bağımsız değişken x ile bağımlı değişken y arasında doğrusal bir ilişki vardır.

2. Bağımsızlık: Artıklar bağımsızdır. Özellikle zaman serisi verilerinde ardışık artıklar arasında bir korelasyon yoktur.

3. Homoskedastisite: Artıklar x’in her seviyesinde sabit bir varyansa sahiptir.

4. Normallik: Model artıkları normal dağılıma sahiptir.

Bu varsayımlardan bir veya daha fazlası karşılanmazsa, doğrusal regresyonumuzun sonuçları güvenilmez ve hatta yanıltıcı olabilir.

Bu yazıda her bir varsayım için bir açıklama, varsayımın karşılanıp karşılanmadığının nasıl belirleneceği ve varsayım karşılanmazsa ne yapılacağına dair açıklamalar sunuyoruz.

Hipotez 1: Doğrusal ilişki

Açıklama

Doğrusal regresyonun ilk varsayımı, bağımsız değişken x ile bağımsız değişken y arasında doğrusal bir ilişki olduğudur.

Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir

Bu varsayımın karşılanıp karşılanmadığını tespit etmenin en basit yolu, x’e karşı y’nin dağılım grafiğini oluşturmaktır. Bu, iki değişken arasında doğrusal bir ilişki olup olmadığını görsel olarak görmenizi sağlar. Grafikteki noktaların düz bir çizgi boyunca uzandığı görülüyorsa, o zaman iki değişken arasında bir tür doğrusal ilişki vardır ve bu varsayım karşılanır.

Örneğin, aşağıdaki grafikteki noktaların düz bir çizgi üzerinde düşmesi x ile y arasında doğrusal bir ilişki olduğunu gösterir:

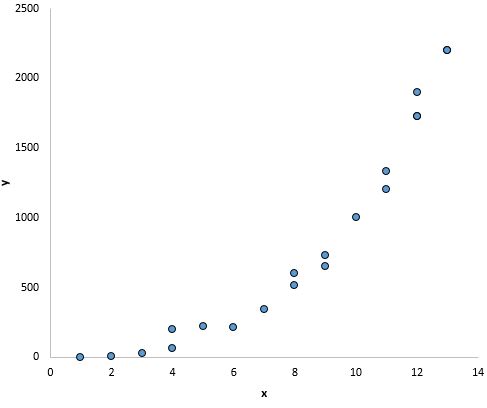
Ancak aşağıdaki grafikte x ile y arasında doğrusal bir ilişki görünmüyor:

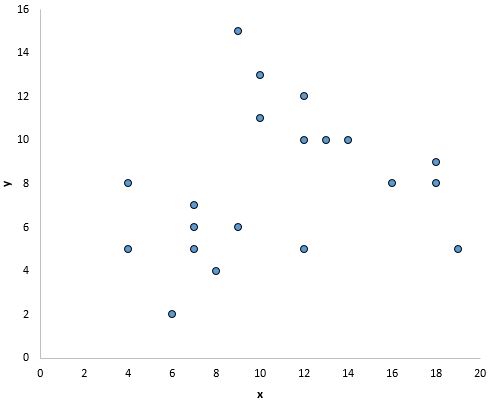
Ve bu grafikte x ile y arasında net bir ilişki var gibi görünüyor ancak doğrusal bir ilişki yok :

Bu varsayıma uyulmazsa ne yapılmalı?

X ve y için değerlerin dağılım grafiğini oluşturursanız ve iki değişken arasında doğrusal bir ilişki olmadığını tespit ederseniz, birkaç seçeneğiniz vardır:

1. Bağımsız ve/veya bağımlı değişkene doğrusal olmayan bir dönüşüm uygulayın. Yaygın örnekler arasında bağımsız ve/veya bağımlı değişkenin logunun, karekökünün veya tersinin alınması yer alır.

2. Modele başka bir bağımsız değişken ekleyin. Örneğin, x’e karşı y’nin grafiği parabolik bir şekle sahipse, modele ek bir bağımsız değişken olarak X ^2’yi eklemek mantıklı olabilir.

Hipotez 2: Bağımsızlık

Açıklama

Doğrusal regresyonun bir sonraki varsayımı, artıkların bağımsız olmasıdır. Bu özellikle zaman serisi verileriyle çalışırken geçerlidir. İdeal olarak ardışık artıklar arasında bir trend olmasını istemeyiz. Örneğin kalıntıların zamanla sürekli olarak artmaması gerekir.

Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir

Bu varsayımın geçerli olup olmadığını test etmenin en basit yolu, artıkların zamana karşı grafiği olan, artıkların zaman serisi grafiğine bakmaktır. İdeal olarak, artık otokorelasyonların çoğu, n’nin örnek boyutu olduğu n’nin karekökünde yaklaşık olarak +/- 2’de yer alan sıfır çevresindeki %95 güven bantları içerisine düşmelidir. Ayrıca Durbin-Watson testini kullanarak bu varsayımın karşılanıp karşılanmadığını resmi olarak test edebilirsiniz.

Bu varsayıma uyulmazsa ne yapılmalı?

Bu varsayımın nasıl ihlal edildiğine bağlı olarak birkaç seçeneğiniz vardır:

• Pozitif seri korelasyon için bağımlı ve/veya bağımsız değişkenin gecikmelerini modele eklemeyi düşünün.
• Negatif seri korelasyon için değişkenlerinizden hiçbirinin aşırı gecikmediğinden emin olun.
• Mevsimsel korelasyon için modele mevsimsel kuklalar eklemeyi düşünün.

Hipotez 3: Homoskedasticity

Açıklama

Doğrusal regresyonun bir sonraki varsayımı, artıkların her x seviyesinde sabit varyansa sahip olduğudur. Buna homoskedastisite denir. Durum böyle olmadığında, artıklar değişen varyanstan muzdariptir.

Bir regresyon analizinde değişen varyans mevcut olduğunda, analiz sonuçlarına inanmak zorlaşır. Spesifik olarak, heteroskedastisite, regresyon katsayısı tahminlerinin varyansını arttırır, ancak regresyon modeli bunu hesaba katmaz. Bu, gerçekte öyle olmadığı halde, bir regresyon modelinin, modeldeki bir terimin istatistiksel olarak anlamlı olduğunu iddia etme olasılığını çok daha artırır.

Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir

Heteroskedasticity’yi tespit etmenin en kolay yolu uygun bir değer/artık grafiği oluşturmaktır.

Bir veri kümesine bir regresyon çizgisi yerleştirdikten sonra, modelin uydurulmuş değerlerini, bu uydurulmuş değerlerin artıklarına karşı gösteren bir dağılım grafiği oluşturabilirsiniz. Aşağıdaki dağılım grafiği, içinde heteroskedastisitenin mevcut olduğu artık değere karşı uygun değerin tipik bir grafiğini göstermektedir.

Takılan değerler arttıkça artıkların nasıl daha fazla yayıldığına dikkat edin. Bu “koni” şekli değişen varyansın klasik bir işaretidir:

Bu varsayıma uyulmazsa ne yapılmalı?

Heteroskedasticity’yi düzeltmenin üç yaygın yolu vardır:

1. Bağımlı değişkeni dönüştürün. Yaygın bir dönüşüm, bağımlı değişkenin logunu almaktır. Örneğin, bir şehirdeki çiçekçi sayısını (bağımlı değişken) tahmin etmek için nüfus büyüklüğünü (bağımsız değişken) kullanırsak, bunun yerine bir kasabadaki çiçekçi sayısının logaritmasını tahmin etmek için nüfus büyüklüğünü kullanmayı deneyebiliriz. Orijinal bağımlı değişken yerine bağımlı değişkenin logunun kullanılması çoğu zaman değişen varyansın ortadan kalkmasıyla sonuçlanır.

2. Bağımlı değişkeni yeniden tanımlayın. Bağımlı değişkeni yeniden tanımlamanın yaygın bir yolu, ham değer yerine bir oran kullanmaktır. Örneğin, bir şehirdeki çiçekçi sayısını tahmin etmek için nüfus büyüklüğünü kullanmak yerine, kişi başına düşen çiçekçi sayısını tahmin etmek için nüfus büyüklüğünü kullanabiliriz. Çoğu durumda bu, çiçekçilerin sayısından ziyade kişi başına düşen çiçekçilerin sayısını ölçtüğümüz için daha büyük popülasyonlarda doğal olarak oluşan değişkenliği azaltır.

3. Ağırlıklı regresyon kullanın. Heteroskedasticity’yi düzeltmenin başka bir yolu da ağırlıklı regresyon kullanmaktır. Bu regresyon türü, her veri noktasına, uydurulan değerin varyansına bağlı olarak bir ağırlık atar. Temel olarak bu, daha yüksek varyansa sahip veri noktalarına düşük ağırlık vererek bunların kalan karelerini azaltır. Uygun ağırlıklar kullanıldığında değişen varyans sorunu ortadan kaldırılabilir.

Hipotez 4: normallik

Açıklama

Doğrusal regresyonun bir sonraki varsayımı, artıkların normal şekilde dağıldığıdır.

Bu varsayımın karşılanıp karşılanmadığı nasıl belirlenir

Bu varsayımın karşılanıp karşılanmadığını kontrol etmenin iki yaygın yolu vardır:

1. QQ grafiklerini kullanarak hipotezi görsel olarak doğrulayın .

Kantil-kantil grafiğinin kısaltması olan QQ grafiği, bir modelin artıklarının normal dağılıma uyup uymadığını belirlemek için kullanabileceğimiz bir grafik türüdür. Grafikteki noktalar kabaca düz bir çapraz çizgi oluşturuyorsa normallik varsayımı karşılanmıştır.

Aşağıdaki QQ grafiği kabaca normal dağılıma uyan bir kalıntı örneğini göstermektedir:

Bununla birlikte, aşağıdaki QQ grafiği, artıkların düz bir çapraz çizgiden açıkça saptığı ve normal dağılıma uymadıklarını gösteren bir durumun örneğini göstermektedir:

2. Normallik varsayımını ayrıca Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre veya D’Agostino-Pearson gibi resmi istatistiksel testleri kullanarak da kontrol edebilirsiniz. Ancak, bu testlerin büyük örneklem boyutlarına duyarlı olduğunu unutmayın; yani, örneklem boyutunuz büyük olduğunda genellikle artıkların normal olmadığı sonucuna varırlar. Bu hipotezi doğrulamak için QQ grafiği gibi grafiksel yöntemleri kullanmanın genellikle daha kolay olmasının nedeni budur.

Bu varsayıma uyulmazsa ne yapılmalı?

Normallik varsayımı karşılanmazsa birkaç seçeneğiniz vardır:

• Öncelikle aykırı değerlerin dağıtım üzerinde büyük bir etkisinin olup olmadığını kontrol edin. Aykırı değerler varsa bunların veri girişi hatası değil, gerçek değerler olduğundan emin olun.
• Daha sonra bağımsız ve/veya bağımlı değişkene doğrusal olmayan bir dönüşüm uygulayabilirsiniz. Yaygın örnekler arasında bağımsız ve/veya bağımlı değişkenin logunun, karekökünün veya tersinin alınması yer alır.

Daha fazla okuma:

Basit Doğrusal Regresyona Giriş
Regresyon Analizinde Heteroskedastisiteyi Anlamak
R’de QQ grafiği nasıl oluşturulur ve yorumlanır