R'de dunnett testi nasıl yapılır

Post hoc testi, hangi grup ortalamalarının birbirinden istatistiksel olarak önemli ölçüde farklı olduğunu belirlemek için ANOVA’nın ardından gerçekleştirilen bir test türüdür.

Çalışma gruplarından biri kontrol grubu olarak kabul edilirse post-hoc test olarak Dunnett testini kullanmalıyız.

Bu eğitimde R’de Dunnett testinin nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: R’de Dunnett testi

Bir öğretmenin, iki yeni çalışma tekniğinin öğrencilerinin sınav puanlarını iyileştirme potansiyeline sahip olup olmadığını bilmek istediğini varsayalım. Bunu test etmek için 30 öğrenciden oluşan sınıfını rastgele aşağıdaki üç gruba ayırır:

• Kontrol grubu: 10 öğrenci
• Yeni teknik çalışma 1: 10 öğrenci
• Yeni teknik çalışma 2: 10 öğrenci

Bir hafta kendilerine verilen çalışma tekniğini kullandıktan sonra her öğrenci aynı sınava girer.

Bir veri seti oluşturmak, grup ortalamalarını görselleştirmek, tek yönlü ANOVA gerçekleştirmek ve son olarak hangi yeni çalışma tekniğinin (varsa) kontrol grubuna kıyasla farklı sonuçlar ürettiğini belirlemek için Dunnett testini gerçekleştirmek için R’de aşağıdaki adımları kullanabiliriz. .

Adım 1: Veri kümesini oluşturun.

Aşağıdaki kod, 30 öğrencinin tamamının sınav sonuçlarını içeren bir veri kümesinin nasıl oluşturulacağını gösterir:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Adım 2: Her grubun sınav sonuçlarını görüntüleyin.

Aşağıdaki kod, her grup için sınav sonuçlarının dağılımını görselleştirmek amacıyla kutu grafiklerinin nasıl oluşturulacağını gösterir:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

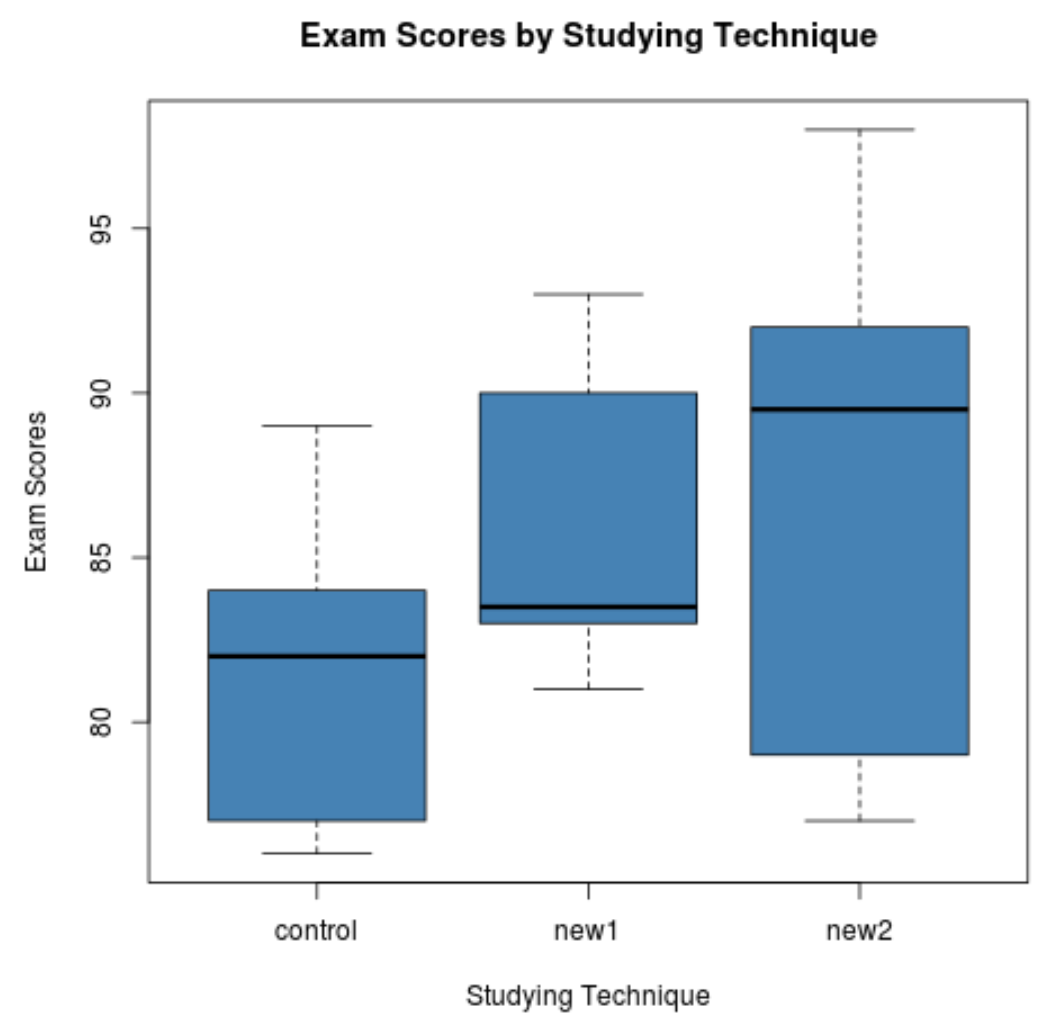
Sadece kutu grafiklerinden sınav puanlarının dağılımının her çalışma tekniği için çok farklı olduğunu görebiliriz. Daha sonra bu farklılıkların istatistiksel olarak anlamlı olup olmadığını belirlemek için tek yönlü bir ANOVA gerçekleştireceğiz.

İlgili: R’de Tek Bir Grafikte Çoklu Kutu Grafiği Nasıl Çizilir

Adım 3: Tek yönlü ANOVA gerçekleştirin.

Aşağıdaki kod, her gruptaki ortalama sınav puanları arasındaki farkları test etmek için tek yönlü ANOVA’nın nasıl gerçekleştirileceğini gösterir:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Genel p değeri ( 0,0476 ) 0,05’ten küçük olduğundan bu durum her grubun aynı ortalama sınav puanına sahip olmadığını gösterir. Daha sonra, hangi çalışma tekniğinin kontrol grubununkinden farklı ortalama sınav puanları ürettiğini belirlemek için Dunnett testini uygulayacağız.

Adım 4: Dunnett testini gerçekleştirin.

R’de Dunnett testini gerçekleştirmek için DescTools kütüphanesindeki aşağıdaki sözdizimini kullanan DunnettTest() fonksiyonunu kullanabiliriz:

Dunnett testi(x, g)

Altın:

• x: veri değerlerinin sayısal bir vektörü (örneğin sınav sonuçları)
• g: Grupların adlarını belirten bir vektör (örn. çalışma tekniği)

Aşağıdaki kod, örneğimiz için bu işlevin nasıl kullanılacağını gösterir:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

Sonucun yorumlanma şekli şu şekildedir:

• Yeni çalışma tekniği 1 ile kontrol grubu arasındaki sınav puanları arasındaki ortalama fark 4,2’dir. Karşılık gelen p değeri 0,1787’dir .
• Yeni çalışma tekniği 2 ile kontrol grubu arasındaki sınav puanları arasındaki ortalama fark 6,4’tür. Karşılık gelen p değeri 0,0296’dır .

Sonuçlara göre, Teknik 2’nin çalışılmasının, kontrol grubundan önemli ölçüde farklı (p = 0,0296) ortalama sınav puanları üreten tek teknik olduğunu görebiliriz.

Ek kaynaklar

Tek Yönlü ANOVA’ya Giriş
R’de tek yönlü ANOVA nasıl gerçekleştirilir
R’de Tukey testi nasıl yapılır?