İki yönlü anova'nın manuel olarak gerçekleştirilmesi
İki faktöre bölünmüş üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için iki yönlü ANOVA kullanılır.
Bu eğitimde iki yönlü ANOVA’nın manuel olarak nasıl gerçekleştirileceği açıklanmaktadır.
Örnek: Manuel iki yönlü ANOVA
Bir botanikçinin bitki büyümesinin güneş ışığına maruz kalma ve sulama sıklığından etkilenip etkilenmediğini bilmek istediğini varsayalım. 40 tohum ekiyor ve bir ay boyunca farklı güneş koşulları ve sulama sıklığı koşullarında büyümelerini sağlıyor.
Bir ay sonra her bitkinin yüksekliğini kaydediyor. Sonuçlar aşağıda gösterilmektedir:

Yukarıdaki tabloda her bir koşul kombinasyonunda beş bitkinin yetiştirildiğini görüyoruz.
Örneğin, beş bitki günlük sulamayla ve güneş ışığı olmadan büyütüldü ve iki ay sonra boyları 4,8 inç, 4,4 inç, 3,2 inç, 3,9 inç ve 4,4 inç oldu:

İki yönlü ANOVA gerçekleştirmek için aşağıdaki adımları kullanabiliriz:
Adım 1: İlk faktörün (sulama sıklığı) karelerinin toplamını hesaplayın
İlk olarak 40 bitkinin genel ortalama yüksekliğini hesaplayacağız:
Genel ortalama = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525
Daha sonra, günlük olarak sulanan tüm bitkilerin ortalama yüksekliğini hesaplayacağız:
Günlük ortalama = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155
Daha sonra, her hafta sulanan tüm bitkilerin ortalama yüksekliğini hesaplayacağız:
Haftalık ortalama = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15
Daha sonra aşağıdaki formülü kullanarak “sulama sıklığı” faktörünün karelerinin toplamını hesaplayacağız:
Σn(X j – X ..) 2
Altın:
- n : j grubunun örneklem büyüklüğü
- Σ : “toplam” anlamına gelen Yunanca bir sembol
- X j : j grubunun ortalaması
- X .. : mükemmel ortalama
Örneğimizde “sulama sıklığı” faktörünün kareler toplamını şu şekilde hesaplıyoruz: 20(5,155-5,1525) 2 + 20(5,15-5,1525) 2 = 0,00025
Adım 2: İkinci faktörün (güneşe maruz kalma) karelerinin toplamını hesaplayın
İlk olarak 40 bitkinin genel ortalama yüksekliğini hesaplayacağız:
Genel ortalama = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525
Daha sonra güneşe maruz kalmayan tüm bitkilerin ortalama yüksekliğini hesaplayacağız:
Güneşsiz ortalama = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07
Çeşitli güneş ışınlarına maruz kalan bitkilerin ortalama yüksekliğini bulmak için bu hesaplamayı tekrarlayacağız:
- Düşük güneş ışığı ortalaması = 5,1
- Ortalama ortalama güneş ışığı = 5,89
- Ortalama yüksek güneş ışığı = 5,55
Daha sonra, aşağıdaki formülü kullanarak “güneşe maruz kalma” faktörünün karelerinin toplamını hesaplayacağız:
Σn(X j – X ..) 2
Altın:
- n : j grubunun örneklem büyüklüğü
- Σ : “toplam” anlamına gelen Yunanca bir sembol
- X j : j grubunun ortalaması
- X .. : mükemmel ortalama
Örneğimizde “güneşe maruz kalma” faktörünün kareler toplamını şu şekilde hesaplıyoruz: 10(4,07-5,1525) 2 + 10(5,1-5,1525) 2 + 10(5,89 -5,1525) 2 + 10(5,55-5,1525) 2 = 18,76475
Adım 3: İçerideki karelerin toplamını hesaplayın (hata)
Daha sonra, her bir faktör kombinasyonu ile bireysel bitki boyları arasındaki farkların karelerinin toplamını alarak karelerin toplamını hesaplayacağız.
Örneğin güneş ışığına maruz kalmadan günlük olarak sulanan tüm bitkilerin ortalama boyu 4,14’tür. Daha sonra bu bireysel bitkilerin her biri için farkların karelerinin toplamını aşağıdaki şekilde hesaplayabiliriz:
- Günlük sulama için ve güneşsiz SS: (4,8-4,14) 2 + (4,4-4,14) 2 + (3,2-4,14) 2 + (3,9-4,14) 2 + (4,4-4,14) 2 = 1,512
Bu işlemi her faktör kombinasyonu için tekrarlayabiliriz:
- Günlük sulama ve düşük güneş ışığı için SS: 0,928
- Günlük sulama ve ortalama güneş ışığı için SS: 1.788
- Günlük sulama ve güçlü güneş ışığı için SS: 1,648
- Güneşsiz haftalık sulama için SS: 0,34
- Haftalık sulama ve az güneş ışığı için SS: 0,548
- Haftalık sulama ve ortalama güneş ışığı için SS: 0,652
- Haftalık sulama ve güçlü güneş ışığı için SS: 1.268
Daha sonra tüm bu değerlerin toplamını alarak içindeki karelerin toplamını bulabiliriz (hata):
= 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684 içindeki karelerin toplamları
Adım 4: Toplam kareler toplamını hesaplayın
Daha sonra her bitkinin boyu ile genel ortalama arasındaki farkların toplamını alarak toplam kareler toplamını hesaplayabiliriz:
Toplam kareler toplamı = (4,8 – 5,1525) 2 + (5 – 5,1525) 2 + … + (5,5 – 5,1525) 2 = 28,45975
Adım 5: Kareler etkileşiminin toplamını hesaplayın
Daha sonra, aşağıdaki formülü kullanarak kareler etkileşiminin toplamını hesaplayacağız:
- Etkileşim SS = SS Toplam – SS Faktör 1 – SS Faktör 2 – SS İç Mekan
- SS etkileşimi = 28,45975 – 0,00025 – 18,76475 – 8,684
- SS etkileşimi = 1.01075
Adım 6: ANOVA tablosunu tamamlayın
Son olarak iki yönlü ANOVA tablosundaki değerleri dolduracağız:
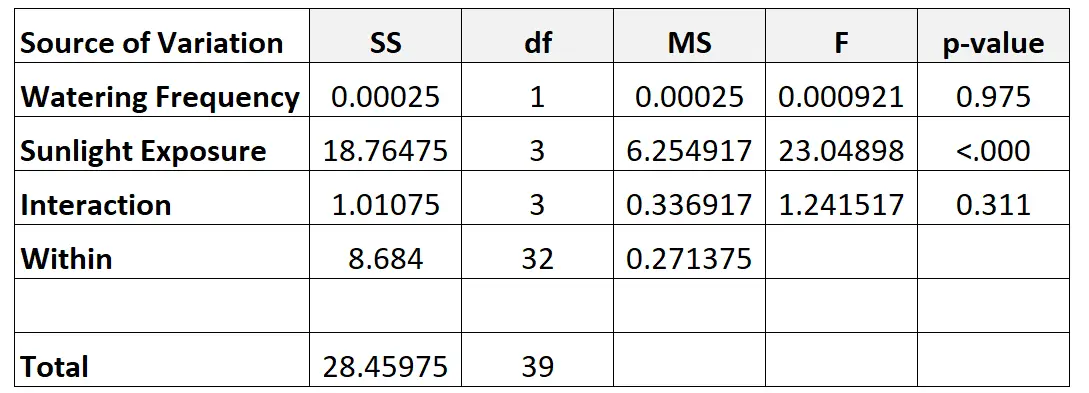
Tablodaki farklı sayıları şu şekilde hesapladık:
- df Sulama sıklığı: d-1 = 2-1 = 1
- df Güneşe maruz kalma: k-1 = 4-1 = 3
- dfEtkileşim : (j-1)*(k-1) = 1*3 = 3
- df In : n – (j*k) = 40 – (2*4) = 32
- toplam sd: n-1 = 40-1 = 39
- MS: SS/DF
- Sulama frekansı F : iç mekan MS/MS sulama frekansı
- F Güneş ışığına maruz kalma : Kapalı alanlarda MS / MS güneş ışığına maruz kalma
- Etkileşim F : Etkileşim MS / MS İçi
- p-değeri sulama frekansı : Payı df = 1 ve paydası df = 32 olan 0,000921 F değerine karşılık gelen p değeri
- Güneşe maruz kalma p-değeri : payı df = 3 ve paydası df = 32 olan 23.04898 F değerine karşılık gelen p değeri
- p-değeri etkileşimi : Payı df = 3 ve paydası df = 32 olan 1,241517’nin F değerine karşılık gelen p değeri
Not #1: n = toplam gözlem sayısı, j = sulama sıklığına ilişkin düzey sayısı, k = güneşe maruz kalma düzeyi sayısı.
Not #2 : F değerine karşılık gelen p değerleri , F dağılımı hesaplayıcısı kullanılarak hesaplanmıştır.
Adım 7: Sonuçları yorumlayın
ANOVA tablosundan şunları gözlemleyebiliriz:
- Sulama sıklığı ile güneşe maruz kalma arasındaki etkileşimin p değeri 0,311 idi. Bu, α = 0,05’te istatistiksel olarak anlamlı değildir.
- Sulama sıklığına ilişkin p değeri 0,975’tir . Bu, α = 0,05’te istatistiksel olarak anlamlı değildir.
- Güneşe maruz kalmanın p değeri <0,000 idi. Bu, α = 0,05’te istatistiksel olarak anlamlıdır.
Bu sonuçlar, bitki boyu üzerinde istatistiksel olarak anlamlı etkiye sahip tek faktörün güneşe maruz kalma olduğunu göstermektedir.
Etkileşim etkisi olmadığından güneşe maruz kalmanın etkisi, sulama sıklığının her seviyesinde tutarlıdır.
Basitçe söylemek gerekirse, bir bitkinin günlük veya haftalık olarak sulanmasının, güneşe maruz kalmanın bitkiyi nasıl etkilediği üzerinde hiçbir etkisi yoktur.
Ek kaynaklar
Aşağıdaki eğitimler ANOVA’lar hakkında ek bilgi sağlar:
Tek yönlü ANOVA manuel olarak nasıl gerçekleştirilir?
Tekrarlanan Ölçümlerin Manuel Olarak Gerçekleştirilmesi ANOVA
Tam Kılavuz: İki Yönlü ANOVA Sonuçları Nasıl Raporlanır?