Elle çoklu doğrusal regresyon (adım adım)
Çoklu doğrusal regresyon, iki veya daha fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanabileceğimiz bir yöntemdir.
Bu eğitimde çoklu doğrusal regresyonun manuel olarak nasıl gerçekleştirileceği açıklanmaktadır.
Örnek: elle çoklu doğrusal regresyon
Bir yanıt değişkeni y ve iki tahmin değişkeni x 1 ve x 2’den oluşan aşağıdaki veri setine sahip olduğumuzu varsayalım:
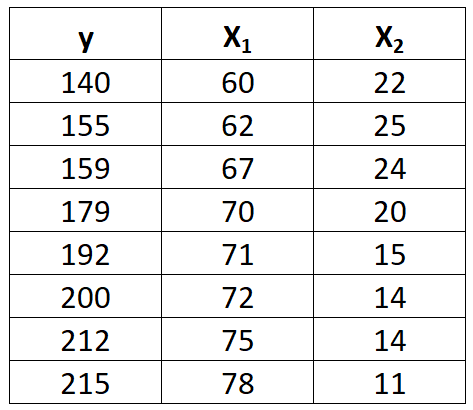
Bu veri kümesine çoklu doğrusal regresyon modelini sığdırmak için aşağıdaki adımları tamamlayın.
Adım 1: x 1 2 , x 2 2 , x 1 y, x 2 y ve x 1 x 2’yi hesaplayın.
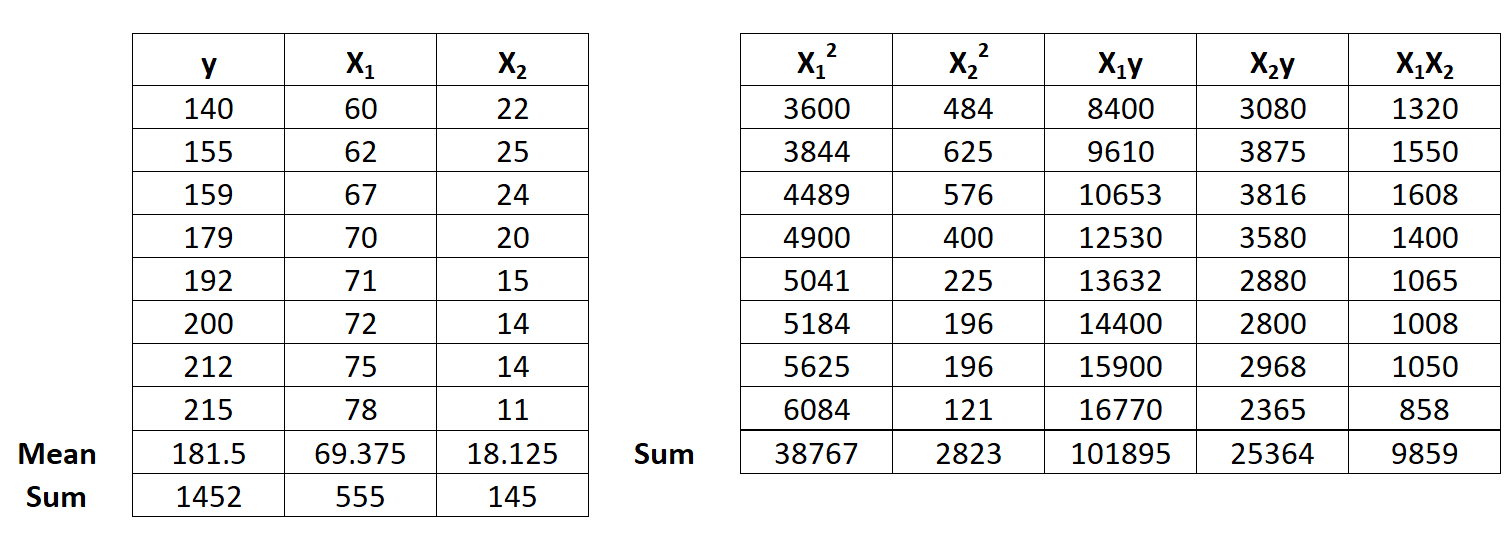
Adım 2: Regresyon toplamlarını hesaplayın.
Daha sonra aşağıdaki regresyon toplamı hesaplamalarını gerçekleştirin:
- Σx12 = ΣX12 – ( ΣX1 ) 2 /n = 38,767 – (555) 2/8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 /n = 2823 – (145) 2/8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
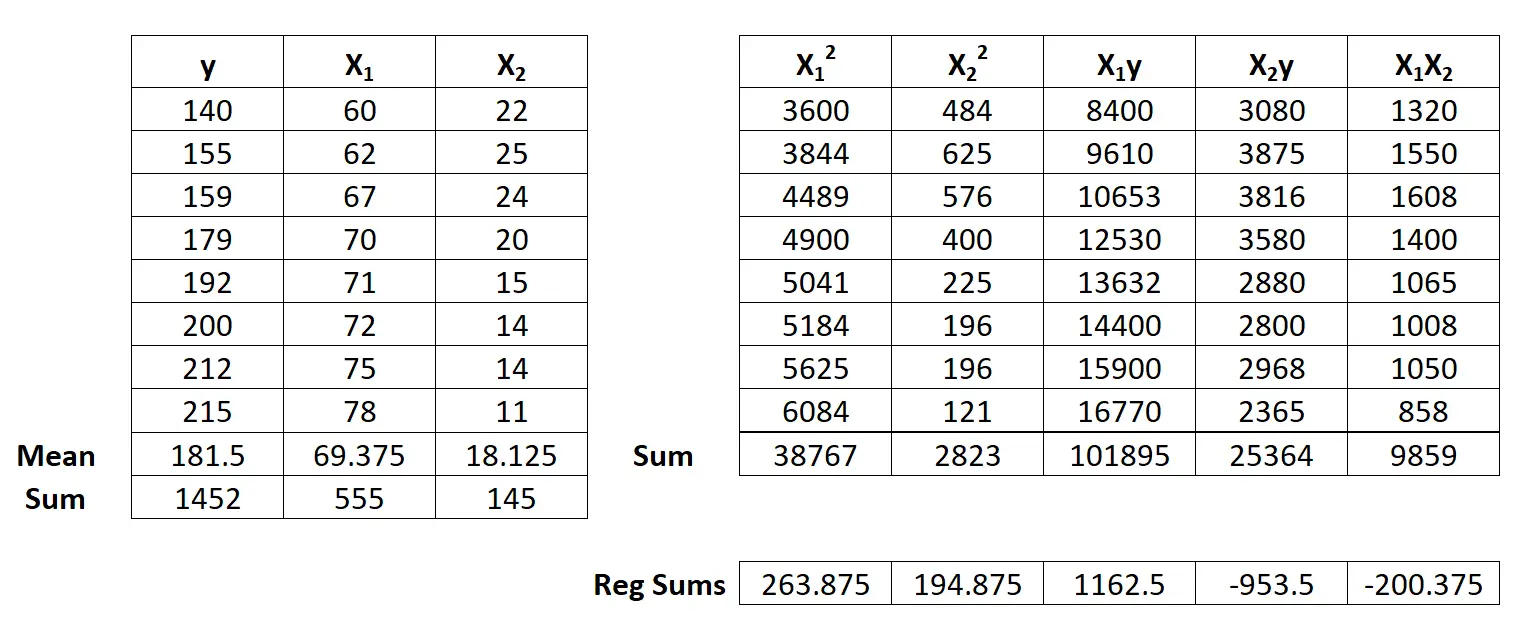
Adım 3: b 0 , b 1 ve b 2’yi hesaplayın.
b 1’i hesaplamak için kullanılan formül şöyledir: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Yani, b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
b 2’yi hesaplama formülü şöyledir: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Yani, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
b 0’ı hesaplama formülü şöyledir: y – b 1 X 1 – b 2 X 2
Böylece, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Adım 5: Tahmin edilen doğrusal regresyon denklemine b 0 , b 1 ve b 2’yi yerleştirin.
Tahmin edilen doğrusal regresyon denklemi şu şekildedir: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
Örneğimizde ŷ = -6,867 + 3,148x 1 – 1,656x 2
Çoklu doğrusal regresyon denklemi nasıl yorumlanır
Bu tahmini doğrusal regresyon denklemini şu şekilde yorumlayabilirsiniz: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Her iki yordayıcı değişken de sıfıra eşit olduğunda y’nin ortalama değeri -6,867’dir.
b1 = 3,148 . X 2’nin sabit kaldığı varsayıldığında, x 1’deki bir birimlik artış, y’deki ortalama 3,148 birimlik artışla ilişkilidir.
b2 = -1,656 . x 1’in sabit kaldığı varsayıldığında, x 2’deki bir birimlik artış, y’deki ortalama 1.656 birimlik azalmayla ilişkilidir.
Ek kaynaklar
Çoklu Doğrusal Regresyona Giriş
Elle basit doğrusal regresyon nasıl gerçekleştirilir
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil