Excel'de eşleştirilmiş örnekler t testi nasıl gerçekleştirilir

Eşleştirilmiş örnekler t-testi, bir örnekteki her gözlemin diğer örnekteki bir gözlemle ilişkilendirilebildiği durumlarda iki örneğin ortalamalarını karşılaştırmak için kullanılır.

Bu eğitimde Excel’de eşleştirilmiş örnekler t testinin nasıl gerçekleştirileceği açıklanmaktadır.

Excel’de eşleştirilmiş örnekler t testi nasıl yapılır

Belirli bir müfredatın, öğrencilerin belirli bir sınavdaki performansı üzerinde önemli bir etkisinin olup olmadığını bilmek istediğimizi varsayalım. Bunu test etmek için bir sınıftaki 20 öğrenciden ön test yapmalarını istiyoruz. Daha sonra her öğrencinin iki hafta boyunca müfredata katılmasını sağlıyoruz. Daha sonra öğrenciler benzer zorluktaki bir testi tekrar alırlar.

Birinci ve ikinci testlerdeki ortalama puanlar arasındaki farkı karşılaştırmak için eşleştirilmiş örneklem t testi kullanıyoruz çünkü her öğrencinin ilk testteki puanı, ikinci testteki puanıyla ilişkilendirilebilir.

Aşağıdaki resimde her öğrencinin ön test puanı ve son test puanı gösterilmektedir:

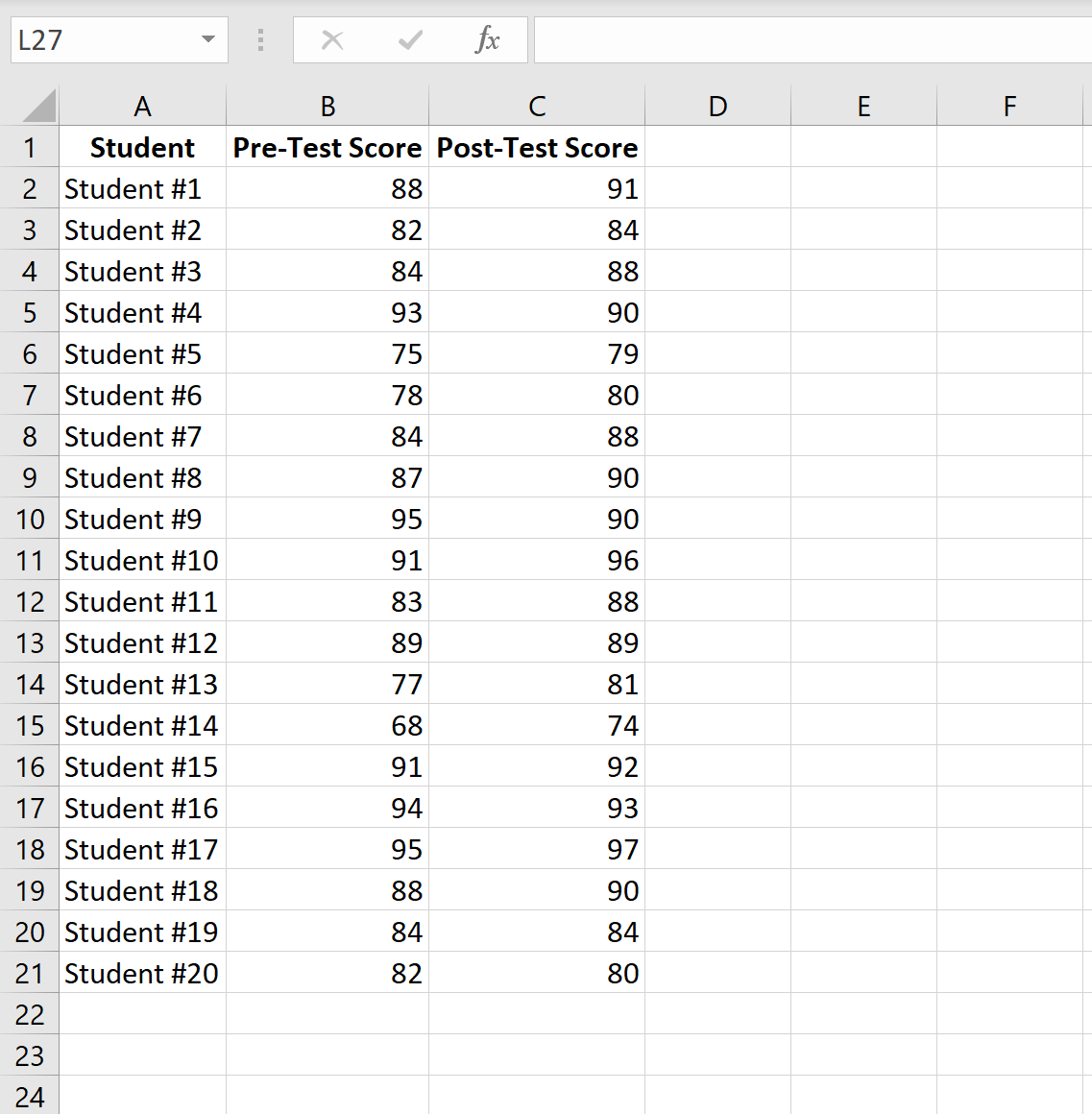
Ön test ve son test arasında ortalama test puanları arasında anlamlı bir fark olup olmadığını belirlemek amacıyla eşleştirilmiş örnekler t testi gerçekleştirmek için aşağıdaki adımları tamamlayın.

Adım 1: Veri Analizi Araç Paketini açın.

Üst şeridin Veri sekmesinde “Veri Analizi”ne tıklayın.

Tıklamak için bu seçeneği göremiyorsanız, öncelikle tamamen ücretsiz olan Analiz Araç Paketi’ni indirmeniz gerekir.

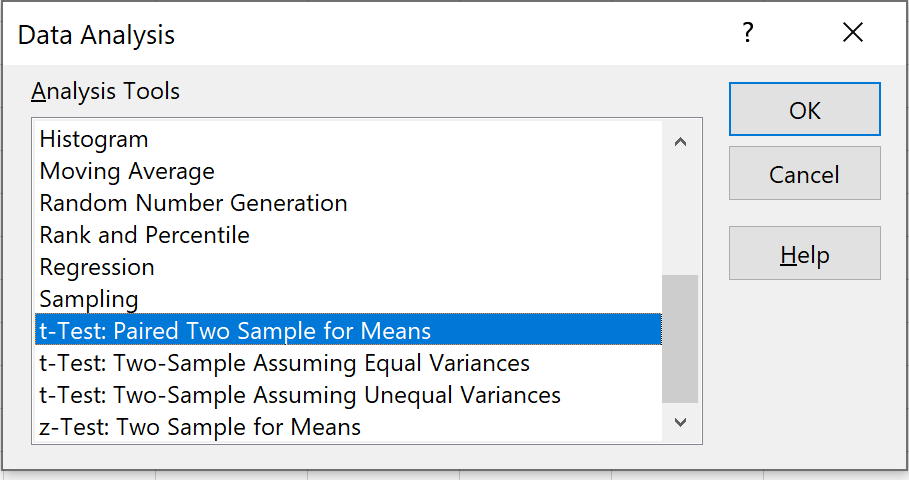
Adım 2: Kullanılacak uygun testi seçin.

T-Test: Paired Two Sample for Means yazan seçeneği seçin ve ardından Tamam’a tıklayın.

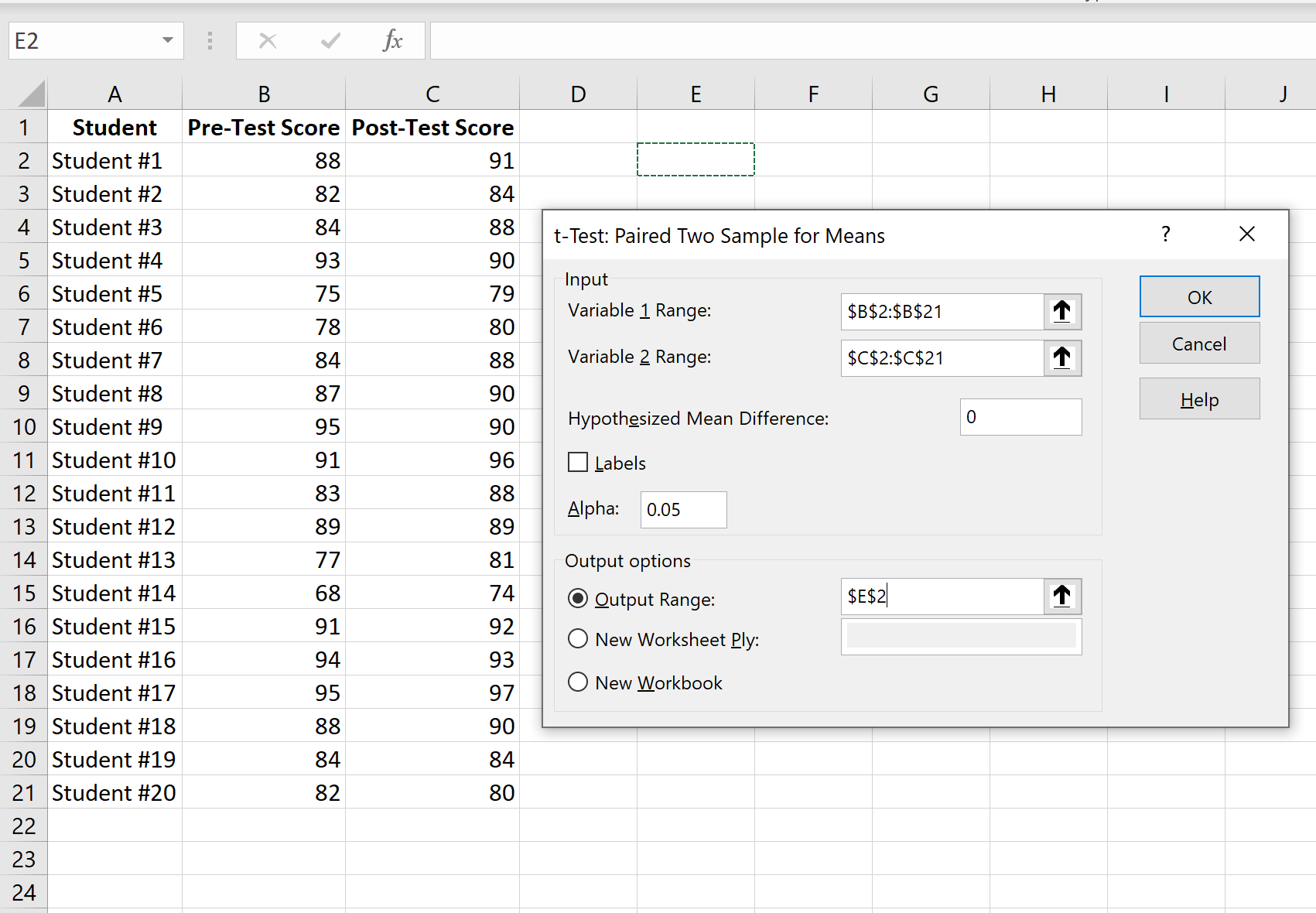
Adım 3: Gerekli bilgileri girin.

Değişken 1 (ön test puanları), değişken 2 (son test puanları) için değer aralığını, varsayımsal ortalama farkı (bu durumda “0” koyarız çünkü gerçek farkın olup olmadığını bilmek istiyoruz) ön test ve son test puanları arasındaki ortalama 0’dır) ve test sonuçlarının görüntülenmesini istediğimiz çıktı aralığıdır. Daha sonra Tamam’ı tıklayın.

Adım 4: Sonuçları yorumlayın.

Önceki adımda Tamam’a tıkladığınızda t-testi sonuçları görüntülenecektir.

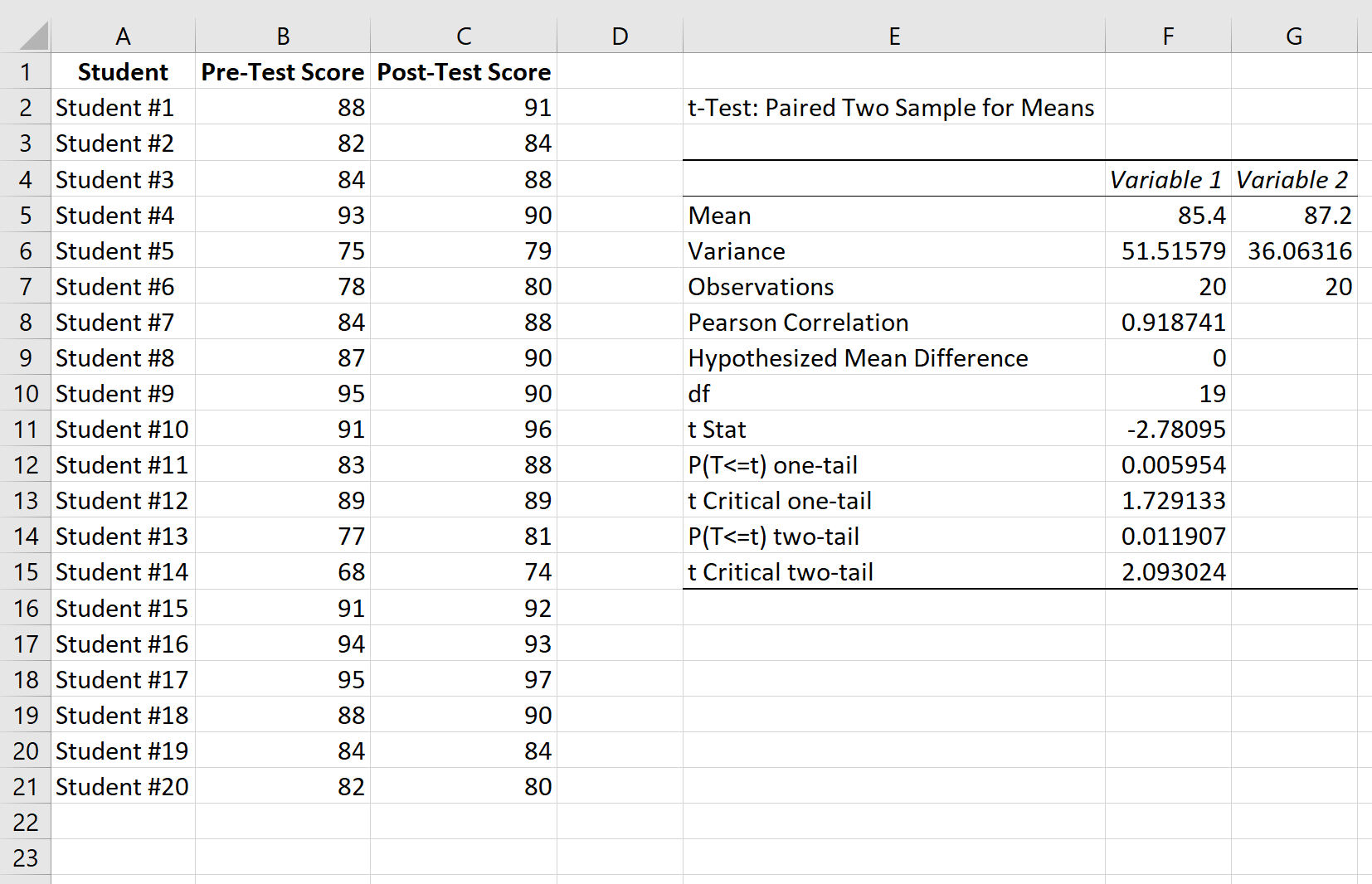
Sonuçları nasıl yorumlayacağınız aşağıda açıklanmıştır:

Ortalama: Bu, her numunenin ortalamasıdır. Ortalama ön test puanı 85,4 , ortalama son test puanı ise 87,2’dir .

Varyans: Bu, her numunenin varyansıdır. Ön test puanlarının varyansı 51.51 , son test puanlarının varyansı ise 36.06’dır .

Gözlemler: Bu, her bir örnekteki gözlemlerin sayısıdır. Her iki örnek de 20 gözlem içermektedir.

Pearson Korelasyonu: Ön test puanları ile son test puanları arasındaki korelasyon. 0,918 olduğu ortaya çıktı.

Varsayımsal Ortalama Farkı: Hakkında “varsayım kurduğumuz” sayı, iki ortalama arasındaki farktır. Bu durumda ön test ve son test puanları arasında fark olup olmadığını test etmek istediğimiz için 0’ı seçtik.

df: t testi için serbestlik derecesi. Bu, n-1 olarak hesaplanır; burada n, çiftlerin sayısıdır. Bu durumda sd = 20 – 1 = 19 olur.

t İstatistik: -2,78 olarak çıkan t- testi istatistiği.

İki kuyruklu P(T<=t): iki kuyruklu t testi için p değeri. Bu durumda p = 0,011907 . Bu alfa = 0,05’ten küçüktür, dolayısıyla sıfır hipotezini reddediyoruz. Ön test ve son test puan ortalamaları arasında istatistiksel olarak anlamlı bir fark olduğunu söyleyecek yeterli kanıtımız var.

t İki Kuyruklu Kritik: Testin kritik değeri olup, alfa = 0,05 ve df = 19 olan iki kuyruklu bir teste karşılık gelen değerin t-dağılımı tablosunda tanımlanmasıyla bulunur. Bu değer 2 olur, 093024 . T testi istatistiğimizin mutlak değeri bu değerden büyük olduğundan sıfır hipotezini reddediyoruz. Ön test ve son test puan ortalamaları arasında istatistiksel olarak anlamlı bir fark olduğunu söyleyecek yeterli kanıtımız var.

Hem p değeri hem de kritik değer yaklaşımının aynı sonuca varacağını unutmayın.

Ek kaynaklar

Aşağıdaki eğitimlerde Excel’de diğer t-testlerinin nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de tek örnek t testi nasıl yapılır
Excel’de iki örnekli t testi nasıl yapılır