Eşleştirilmiş t testinde formüle edilen üç hipotez

Eşleştirilmiş örnekler t-testi, bir örnekteki her gözlemin diğer örnekteki bir gözlemle ilişkilendirilebildiği durumlarda iki örneğin ortalamalarını karşılaştırmak için kullanılır.

Bu test türü verilerle ilgili aşağıdaki varsayımları yapar:

1. Bağımsızlık: Her gözlem diğer gözlemlerden bağımsız olmalıdır.

2. Normallik: Çiftler arasındaki farklar yaklaşık olarak normal dağılmalıdır.

3. Aşırı aykırı değerler olmamalıdır: Farklılıklar arasında aşırı aykırı değerler olmamalıdır.

Bu varsayımlardan bir veya daha fazlası karşılanmazsa eşleştirilmiş örnekler t-testinin sonuçları güvenilmez veya yanıltıcı olabilir.

Bu derste, her bir varsayımın açıklamasını, varsayımın karşılanıp karşılanmadığının nasıl belirleneceğini ve ihlal edilmesi durumunda ne yapılacağını açıklıyoruz.

Hipotez 1: Bağımsızlık

Eşleştirilmiş örnekler t testi, her gözlemin diğer tüm gözlemlerden bağımsız olduğunu varsayar.

Bu hipotez nasıl doğrulanır?

Bu varsayımı doğrulamanın en basit yolu, her gözlemin rastgele örnekleme yöntemi kullanılarak toplandığını doğrulamaktır.

Rastgele bir örnekleme yöntemi kullanılmışsa (basit rastgele örnekleme gibi), her gözlemin diğer tüm gözlemlerden bağımsız olduğunu varsayabiliriz.

Bu varsayıma uyulmazsa ne yapılmalı?

Bu varsayım karşılanmazsa eşleştirilmiş örnekler t-testinin sonuçları tamamen geçersizdir.

Bu senaryoda, her gözlemin bağımsız olmasını sağlamak için rastgele örnekleme yöntemini kullanarak yeni gözlemler toplamak en iyisidir.

Hipotez 2: normallik

Eşleştirilmiş örnekler t-testi, çiftler arasındaki farkların yaklaşık olarak normal şekilde dağılması gerektiğini varsayar.

Bu çok önemli bir varsayımdır çünkü çiftler arasındaki farklar normal şekilde dağılmıyorsa, sonuç çıkarmak için testin p değerini kullanmak geçerli değildir.

Bu hipotez nasıl doğrulanır?

Bu hipotezi test etmenin en kolay yolu, eşleştirilmiş farklılıkların bir histogramını oluşturmak ve histogramın çan şekline sahip olup olmadığını görsel olarak kontrol etmektir.

Örneğin histogram şu şekilde görünüyorsa normallik varsayımının karşılandığını söyleyebiliriz:

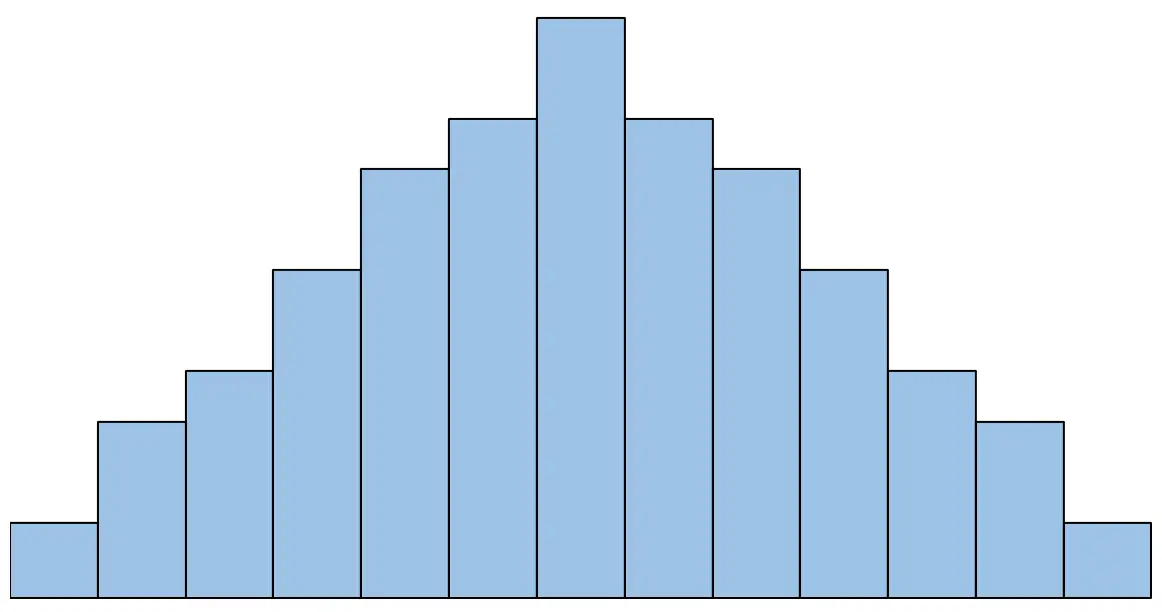
Ancak histogram şu şekilde görünüyorsa normallik varsayımının karşılanmadığını söyleyebiliriz:

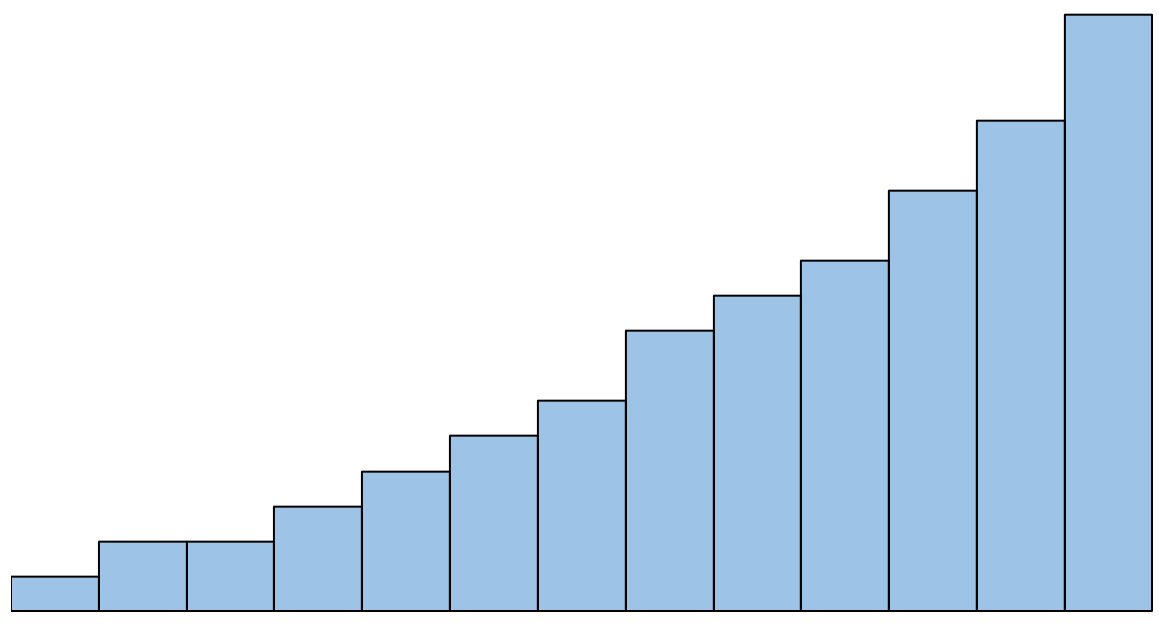
Bu varsayıma uyulmazsa ne yapılmalı?

Bu varsayımın ihlal edilmesi durumunda, eşleştirilmiş örnekler t-testinin parametrik olmayan eşdeğeri olarak kabul edilen ve eşleştirilmiş farkların normal şekilde dağıldığını varsaymayan Wilcoxon işaretli sıra testi gerçekleştirebiliriz.

Hipotez 3: aşırı aykırı değerler yok

Eşleştirilmiş örnekler t testi, verilerde aşırı aykırı değerlerin olmadığını varsayar.

Bu hipotez nasıl doğrulanır?

Bu hipotezi test etmenin en kolay yolu, eşleştirilmiş farklılıkların bir kutu grafiğini oluşturmak ve herhangi bir aykırı değer olup olmadığını görsel olarak kontrol etmektir.

Örneğin, eşleştirilmiş farkların kutu grafiğinin şöyle göründüğünü varsayalım:

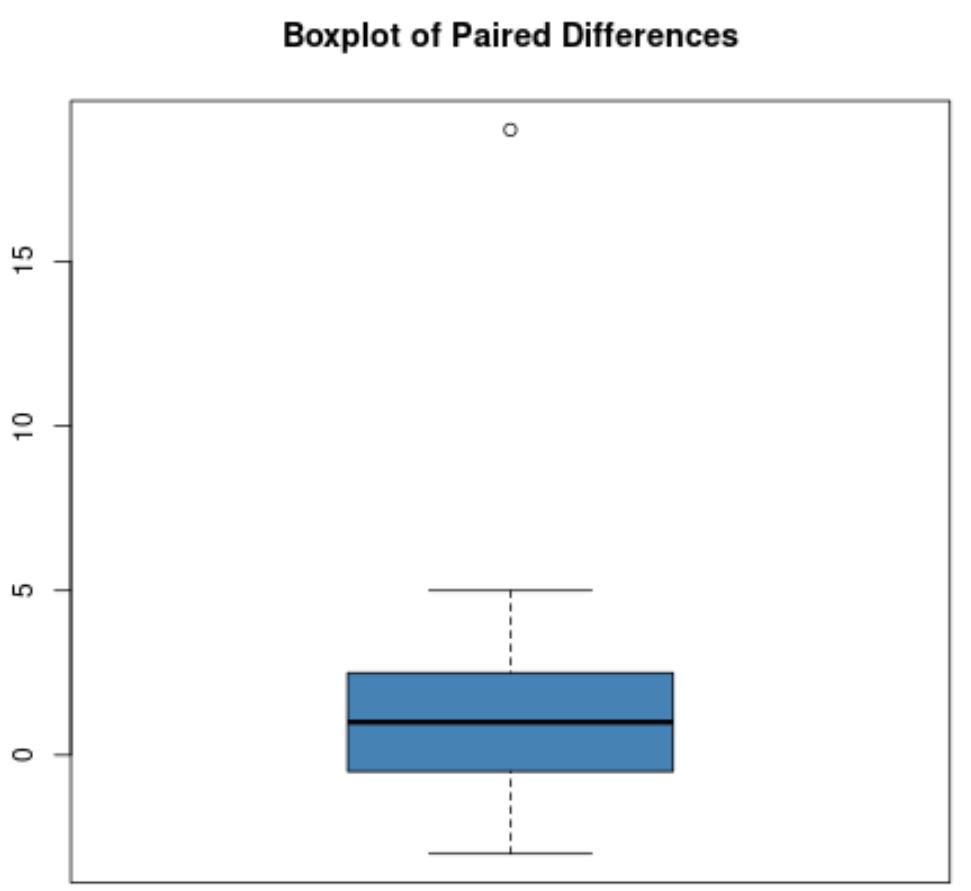
Eşleştirilmiş farkların çoğu sıfıra yakındır, ancak yaklaşık 19’a eşit bir eşleştirilmiş fark vardır ki bu açıkça aykırıdır.

Not : Bir daire genellikle kutu grafiğinde aykırı bir değeri belirtmek için kullanılır.

Bununla birlikte, eşleştirilmiş farkların kutu grafiğinin şöyle göründüğünü varsayalım:

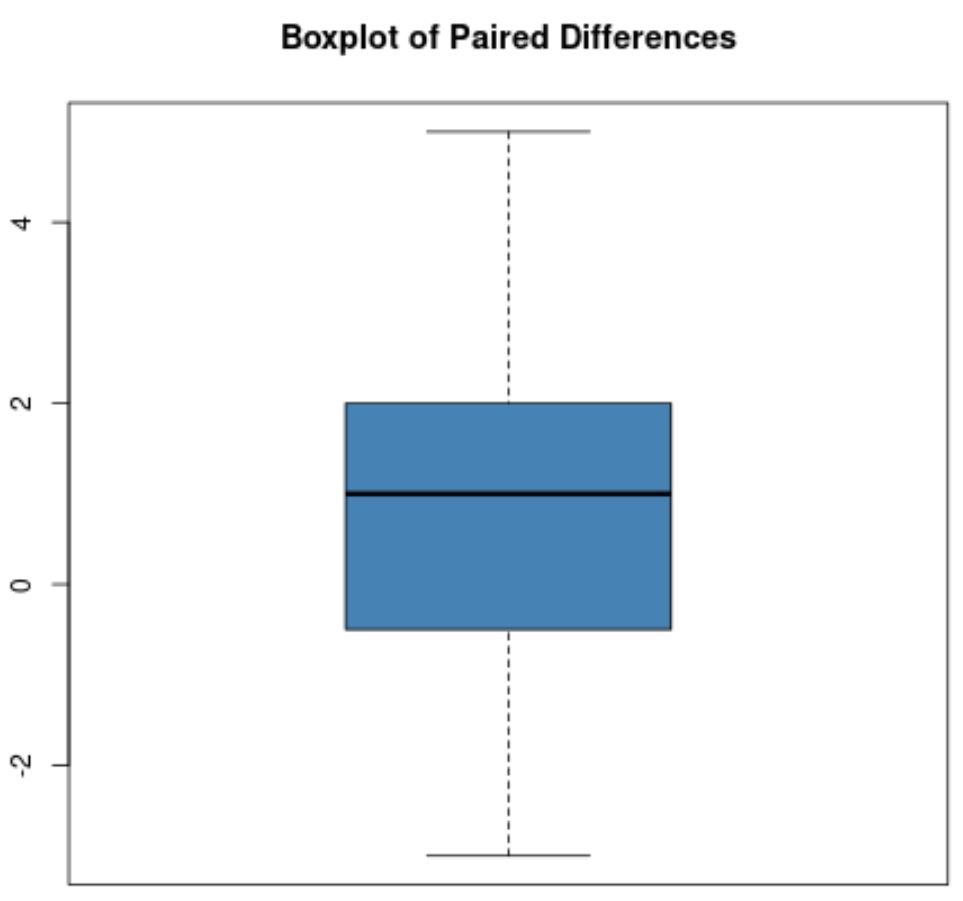
Bu kutu grafiğinde belirgin aykırı değerler yoktur, dolayısıyla verilerde aşırı aykırı değerlerin olmadığını varsayacağız.

Bu varsayıma uyulmazsa ne yapılmalı?

Bu varsayım ihlal edilirse, eşleştirilmiş örnekler t-testinin sonuçları aykırı değerden anormal şekilde etkilenebilir.

Bu senaryoda, hatalı bir veri noktasını temsil ettiğini veya bir veri girişi hatasının sonucu olduğunu düşünüyorsanız aykırı değeri kaldırabilirsiniz.

Alternatif olarak, aykırı değeri saklayabilir ve eşleştirilmiş örnekler t-testi sonuçlarını rapor ederken bunu not edebilirsiniz.

Ek kaynaklar

Aşağıdaki eğitimlerde diğer istatistiksel testlerde yapılan varsayımlar açıklanmaktadır:

Bir t testinde formüle edilen dört hipotez
Ki-kare testinin dört hipotezi
Parametrik testlerin dört hipotezi