Etki boyutu: nedir ve neden önemlidir?
“İstatistiksel anlamlılık, sonuçlarla ilgili en az ilginç olan şey. Sonuçları büyüklük ölçümleri açısından tanımlamanız gerekir; bir tedavi yalnızca insanları etkilemez, aynı zamanda onları ne kadar etkiler. -Gene V. Cam
İstatistiklerde, iki grup arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için sıklıkla p değerlerini kullanırız.
Örneğin, iki farklı çalışma tekniğinin farklı test puanlarına yol açıp açmadığını bilmek istediğimizi varsayalım. Yani, bir teste hazırlanmak için bir çalışma tekniğini kullanan 20 öğrenciden oluşan bir grubumuz var, diğer 20 öğrenciden oluşan bir grup ise farklı bir çalışma tekniğini kullanıyor. Daha sonra her öğrenciye aynı testi uyguluyoruz.
Ortalamalardaki farkı belirlemek için iki örnekli bir t testi çalıştırdıktan sonra testin p değerinin 0,001 olduğunu bulduk. Anlamlılık düzeyi olarak 0,05 kullanırsak bu, iki grubun ortalama sonuçları arasında istatistiksel olarak anlamlı bir fark olduğu anlamına gelir. Dolayısıyla çalışma tekniğinin test sonuçları üzerinde etkisi vardır.
Ancak p değeri bize çalışma tekniğinin test puanları üzerinde etkisi olduğunu söylese de bu etkinin büyüklüğünü söylemez. Bunu anlamak için etki büyüklüğünü bilmemiz gerekir.
Etki büyüklüğü nedir?
Etki büyüklüğü, iki grup arasındaki farkı ölçmenin bir yoludur.
Bir p değeri bize iki grup arasında istatistiksel olarak anlamlı bir fark olup olmadığını söyleyebilirken, etki büyüklüğü bize bu farkın gerçekte ne kadar büyük olduğunu söyleyebilir. Uygulamada etki büyüklükleri, p-değerlerinden çok daha ilginç ve faydalıdır.
Yaptığınız analizin türüne bağlı olarak etki büyüklüğünü ölçmenin üç yolu vardır:
1. Standartlaştırılmış ortalama fark
İki grup arasındaki ortalama farkı incelemek istediğinizde etki büyüklüğünü hesaplamanın uygun yolu standartlaştırılmış bir ortalama fark kullanmaktır. Kullanılacak en popüler formül Cohen’in d’si olarak bilinir ve şu şekilde hesaplanır:
Cohen’in D = ( x1 – x2 )/ s
burada x 1 ve x 2 sırasıyla grup 1 ve grup 2’nin örnek ortalamalarıdır ve s , iki grubun seçildiği popülasyonun standart sapmasıdır.
Bu formülü kullanarak etki büyüklüğünün yorumlanması kolaydır:
- A d’ nin 1 olması, iki grubun ortalamalarının bir standart sapma kadar farklı olduğunu gösterir.
- A d 2, grup ortalamalarının iki standart sapma kadar farklı olduğu anlamına gelir.
- 2,5’lik bir d, iki ortalamanın 2,5 standart sapma kadar farklı olduğunu gösterir ve bu böyle devam eder.
Etki büyüklüğünü yorumlamanın başka bir yolu şudur: 0,3’lük bir etki büyüklüğü, Grup 2’deki ortalama kişinin puanının, grup 1’in kişi ortalamasının 0,3 standart sapma üzerinde olduğu ve dolayısıyla grup 1’in puanlarının %62’sini aştığı anlamına gelir. .
Aşağıdaki tabloda farklı etki boyutları ve bunlara karşılık gelen yüzdelikler gösterilmektedir:
| Etki boyutu | Grup 1’deki kişilerin ortalamasının altında olabilecek grup 2’nin yüzdesi |
|---|---|
| 0,0 | %50 |
| 0,2 | %58 |
| 0,4 | %66 |
| 0,6 | %73 |
| 0,8 | %79 |
| 1.0 | %84 |
| 1.2 | %88 |
| 1.4 | %92 |
| 1.6 | %95 |
| 1.8 | %96 |
| 2.0 | %98 |
| 2.5 | %99 |
| 3.0 | %99,9 |
Etki büyüklüğü ne kadar büyük olursa, her gruptaki ortalama birey arasındaki fark da o kadar büyük olur.
Genel olarak, 0,2 veya daha düşük bir d küçük etki büyüklüğü olarak kabul edilir, 0,5 civarındaki bir d orta etki büyüklüğü olarak kabul edilir ve 0,8 veya daha büyük bir d büyük etki büyüklüğü olarak kabul edilir.
Dolayısıyla, iki grubun ortalamaları en az 0,2 standart sapma kadar farklılık göstermiyorsa, p değeri istatistiksel olarak anlamlı olsa bile fark önemsizdir.
2. Korelasyon katsayısı
İki değişken arasındaki niceliksel ilişkiyi incelemek istediğinizde etki büyüklüğünü hesaplamanın en yaygın yolu Pearson korelasyon katsayısını kullanmaktır. İki değişken X ve Y arasındaki doğrusal ilişkinin bir ölçüsüdür. -1 ile 1 arasında bir değere sahiptir; burada:
- -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
- 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
- 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir
Pearson korelasyon katsayısını hesaplama formülü oldukça karmaşıktır ancak ilgilenenler için burada bulunabilir.
Korelasyon katsayısı sıfırdan ne kadar uzaksa, iki değişken arasındaki doğrusal ilişki o kadar güçlüdür. Bu aynı zamanda X ve Y değişkenlerinin değerlerinin basit bir dağılım grafiğini oluşturarak da görülebilir.
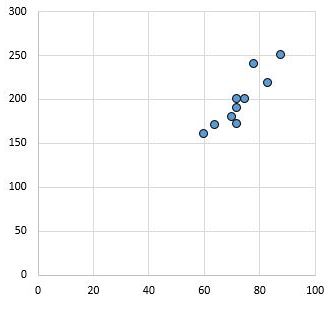
Örneğin, aşağıdaki dağılım grafiği r = 0,94 korelasyon katsayısına sahip iki değişkenin değerlerini göstermektedir.
Bu değerin sıfırdan uzak olması iki değişken arasında pozitif yönde güçlü bir ilişkinin olduğunu göstermektedir.
Tersine, aşağıdaki dağılım grafiği r = 0,03 korelasyon katsayısına sahip iki değişkenin değerlerini göstermektedir. Bu değerin sıfıra yakın olması iki değişken arasında neredeyse hiç ilişki olmadığını göstermektedir.
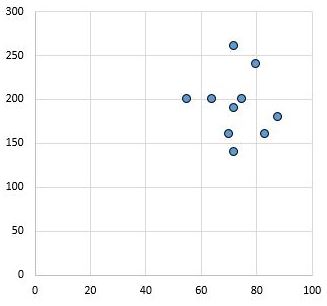
Genel olarak, Pearson korelasyon katsayısının değeri r yaklaşık 0,1 ise etki büyüklüğü küçük, r yaklaşık 0,3 ise orta ve r 0,5’e eşit veya daha büyükse büyük olarak kabul edilir.
3. Oran oranı
Bir tedavi grubundaki başarı olasılığını bir kontrol grubundaki başarı olasılığına karşı incelemek istediğinizde, etki büyüklüğünü hesaplamanın en yaygın yolu olasılık oranını kullanmaktır.
Örneğin aşağıdaki tabloya sahip olduğumuzu varsayalım:
| Etki boyutu | #Başarı | #Satranç |
|---|---|---|
| Tedavi grubu | SAHİP OLMAK | B |
| Kontrol grubu | VS | D |
Olasılık oranı şu şekilde hesaplanacaktır:
Olasılık oranı = (AD) / (BC)
Olasılık oranı 1’den ne kadar uzak olursa, tedavinin gerçek bir etki yaratma olasılığı da o kadar yüksek olur.
P Değerleri Üzerinden Etki Büyüklüğü Kullanmanın Yararları
Etki büyüklüklerinin p değerlerine göre çeşitli avantajları vardır:
1. Etki büyüklüğü, iki grup arasındaki farkın ne kadar büyük olduğu veya iki grup arasındaki ilişkinin ne kadar güçlü olduğu konusunda daha iyi bir fikir edinmemize yardımcı olur. Bir p değeri bize yalnızca anlamlı bir farkın veya anlamlı bir ilişkinin olup olmadığını söyleyebilir.
2. P değerlerinden farklı olarak etki büyüklükleri, farklı ortamlarda yürütülen farklı çalışmaların sonuçlarını niceliksel olarak karşılaştırmak için kullanılabilir. Bu nedenle meta-analizlerde etki büyüklükleri sıklıkla kullanılmaktadır.
3. P değerleri büyük örneklem boyutlarından etkilenebilir. Örneklem büyüklüğü ne kadar büyük olursa, hipotez testinin istatistiksel gücü de o kadar büyük olur ve küçük etkileri bile tespit etmesine olanak tanır. Bu, pratik önemi olmayan küçük etki boyutlarına rağmen düşük p değerlerine yol açabilir.
Basit bir örnek bunu açıkça gösterebilir: Diyelim ki iki çalışma tekniğinin farklı test puanlarına yol açıp açmadığını bilmek istiyoruz. Bir çalışma tekniğini kullanan 20 öğrenciden oluşan bir grubumuz var, farklı bir çalışma tekniğini kullanan 20 öğrenciden oluşan başka bir grubumuz var. Daha sonra her öğrenciye aynı testi uyguluyoruz.
1. grubun ortalama puanı 90.65 , 2. grubun ortalama puanı 90.75’tir . 1. numunenin standart sapması 2,77 ve 2. numunenin standart sapması 2,78’dir .
Bağımsız iki örnekli t testi yaptığımızda test istatistiğinin -0,113 ve buna karşılık gelen p değerinin 0,91 olduğu ortaya çıkıyor. Ortalama test puanları arasındaki fark istatistiksel olarak anlamlı değildir.
Bununla birlikte, iki numunenin numune boyutlarının her ikisinin de 200 olduğunu, ancak ortalamaların ve standart sapmaların tamamen aynı kaldığını düşünün.
Bu durumda, bağımsız iki örnekli bir t testi, test istatistiğinin -1,97 olduğunu ve karşılık gelen p değerinin 0,05’in hemen altında olduğunu ortaya çıkaracaktır. Ortalama test puanları arasındaki fark istatistiksel olarak anlamlıdır.
Büyük örneklem büyüklüklerinin istatistiksel olarak anlamlı sonuçlara yol açmasının altında yatan neden, t- testi istatistiklerini hesaplamak için kullanılan formülden kaynaklanmaktadır:
test istatistiği t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
n 1 ve n 2 küçük olduğunda t testi istatistiğinin tamsayı paydasının küçük olduğuna dikkat edin. Ve küçük bir sayıya böldüğünüzde büyük bir sayı elde edersiniz. Bu, t- testi istatistiğinin büyük olacağı ve karşılık gelen p değerinin küçük olacağı ve dolayısıyla istatistiksel olarak anlamlı sonuçlara yol açacağı anlamına gelir.
İyi bir etki büyüklüğü olarak kabul edilen şey nedir?
Öğrencilerin sıklıkla sorduğu soru şudur: İyi etki büyüklüğü nedir?
Kısa cevap: Bir etki büyüklüğü “iyi” veya “kötü” olamaz çünkü yalnızca iki grup arasındaki farkın boyutunu veya iki grup arasındaki ilişkinin gücünü ölçer.
Ancak bir etkinin büyüklüğünün küçük, orta veya büyük olup olmadığını ölçmek için aşağıdaki temel kuralları kullanabiliriz:
Cohen’in D’si:
- 0,2 veya daha düşük bir d, küçük bir etki büyüklüğü olarak kabul edilir.
- 0,5’lik bir d orta etki büyüklüğü olarak kabul edilir.
- 0,8 veya daha büyük bir d, büyük bir etki büyüklüğü olarak kabul edilir.
Pearson Korelasyon Katsayısı
- r’nin 0,1 civarındaki mutlak değeri küçük bir etki büyüklüğü olarak kabul edilir.
- r’nin 0,3 civarındaki mutlak değeri orta etki büyüklüğü olarak kabul edilir.
- r’nin 0,5’ten büyük mutlak değeri, büyük bir etki büyüklüğü olarak kabul edilir.
Ancak “güçlü” bir korelasyonun tanımı bir alandan diğerine farklılık gösterebilir. Farklı endüstriler arasında neyin güçlü bir korelasyon olarak kabul edildiğini daha iyi anlamak için bu makaleye bakın.