Excel'de korelasyon matrisi nasıl oluşturulur ve yorumlanır

İki değişken arasındaki ilişkiyi ölçmenin bir yolu , iki değişken arasındaki doğrusal ilişkinin bir ölçüsü olan Pearson korelasyon katsayısını kullanmaktır.

-1 ile 1 arasında bir değere sahiptir; burada:

• -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
• 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
• 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir

Korelasyon katsayısı sıfırdan ne kadar uzaksa, iki değişken arasındaki ilişki o kadar güçlüdür.

Ancak bazı durumlarda birden fazla değişken çifti arasındaki korelasyonu anlamak isteriz.

Bu durumlarda, değişkenlerin çeşitli ikili kombinasyonları arasındaki korelasyon katsayılarını gösteren kare bir tablo olan birkorelasyon matrisi oluşturabiliriz.

Bu eğitimde Excel’de bir korelasyon matrisinin nasıl oluşturulacağı ve yorumlanacağı açıklanmaktadır.

Excel’de Korelasyon Matrisi Nasıl Oluşturulur

Diyelim ki 10 basketbolcunun ortalama sayı, ribaund ve asist sayılarını gösteren aşağıdaki veri setine sahibiz:

Bu veri kümesi için bir korelasyon matrisi oluşturmak için Excel’in üst şeridindeki Veri sekmesine gidin ve Veri Analizi’ni tıklayın.

Bu seçeneği görmüyorsanız, öncelikle ücretsiz Veri Analizi Araç Paketini Excel’e yüklemelisiniz .

Görüntülenen yeni pencerede Korelasyon’u seçin ve Tamam’a tıklayın.

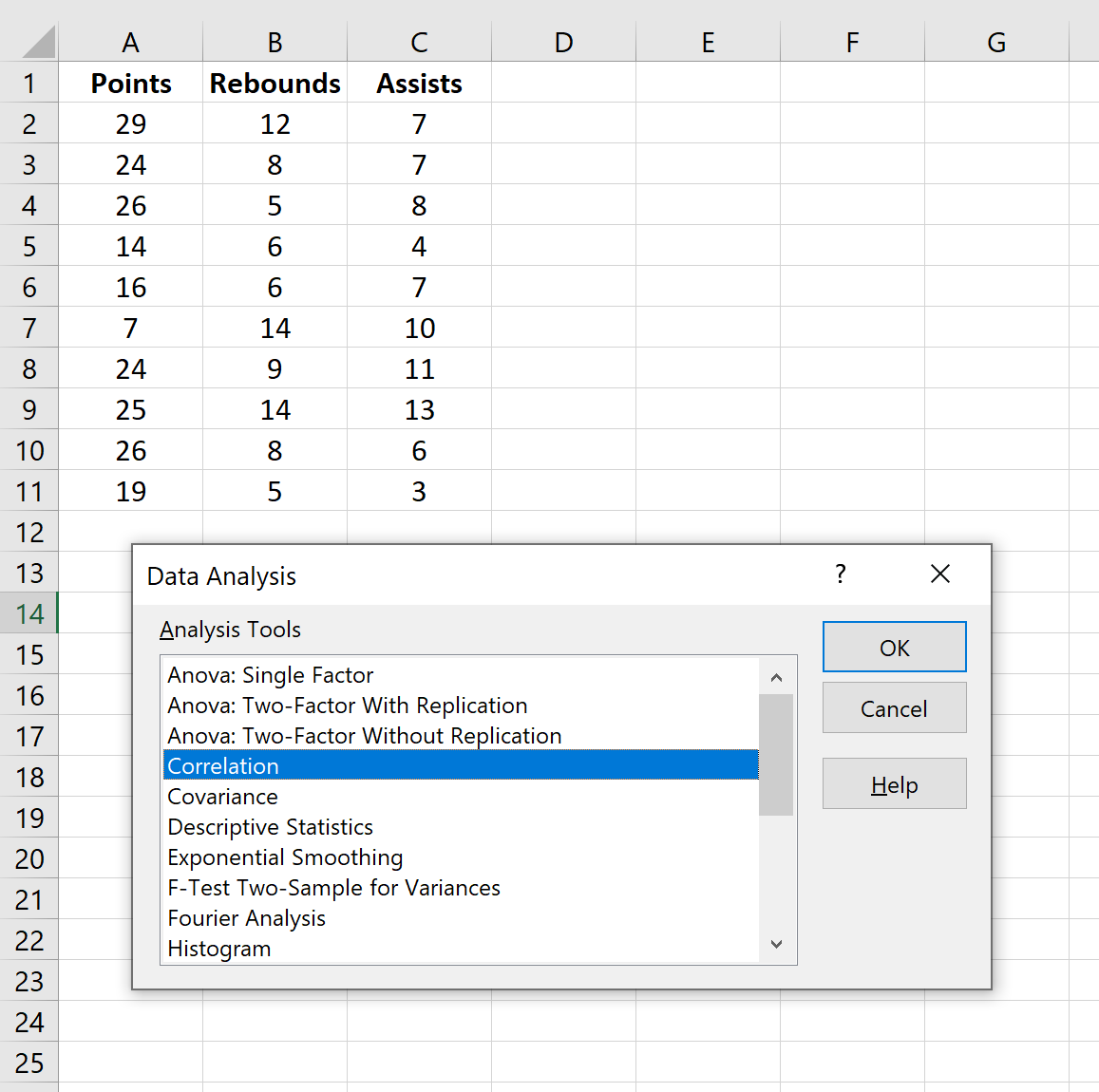
Giriş Aralığı için verilerin bulunduğu hücreleri seçin (etiketlerin bulunduğu ilk satır dahil). İlk satırdaki Etiketler’in yanındaki kutuyu işaretleyin. Çıkış Aralığı için korelasyon matrisinin görünmesini istediğiniz hücreyi seçin. Daha sonra Tamam’ı tıklayın.

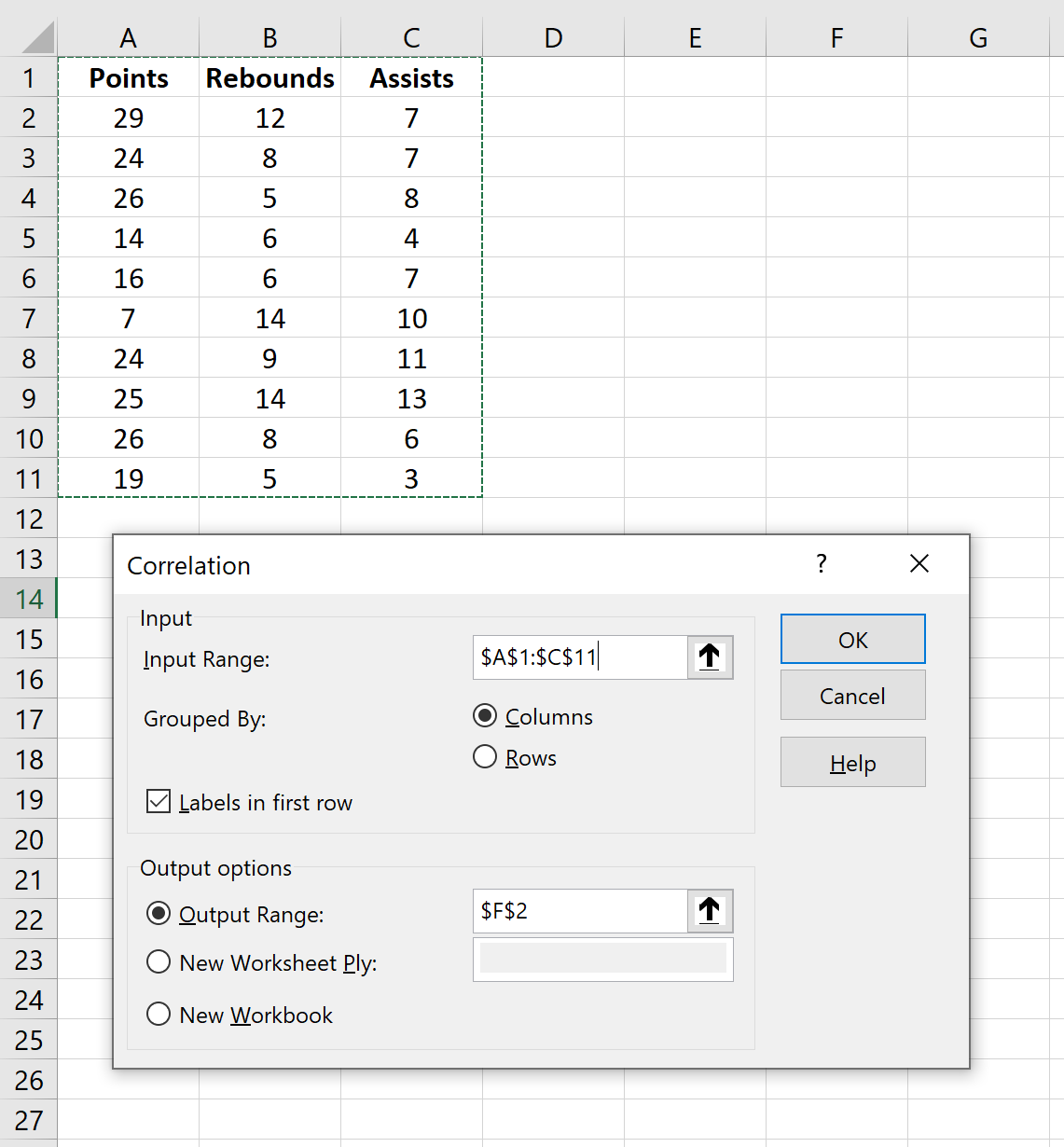
Bu otomatik olarak aşağıdaki korelasyon matrisini üretecektir:

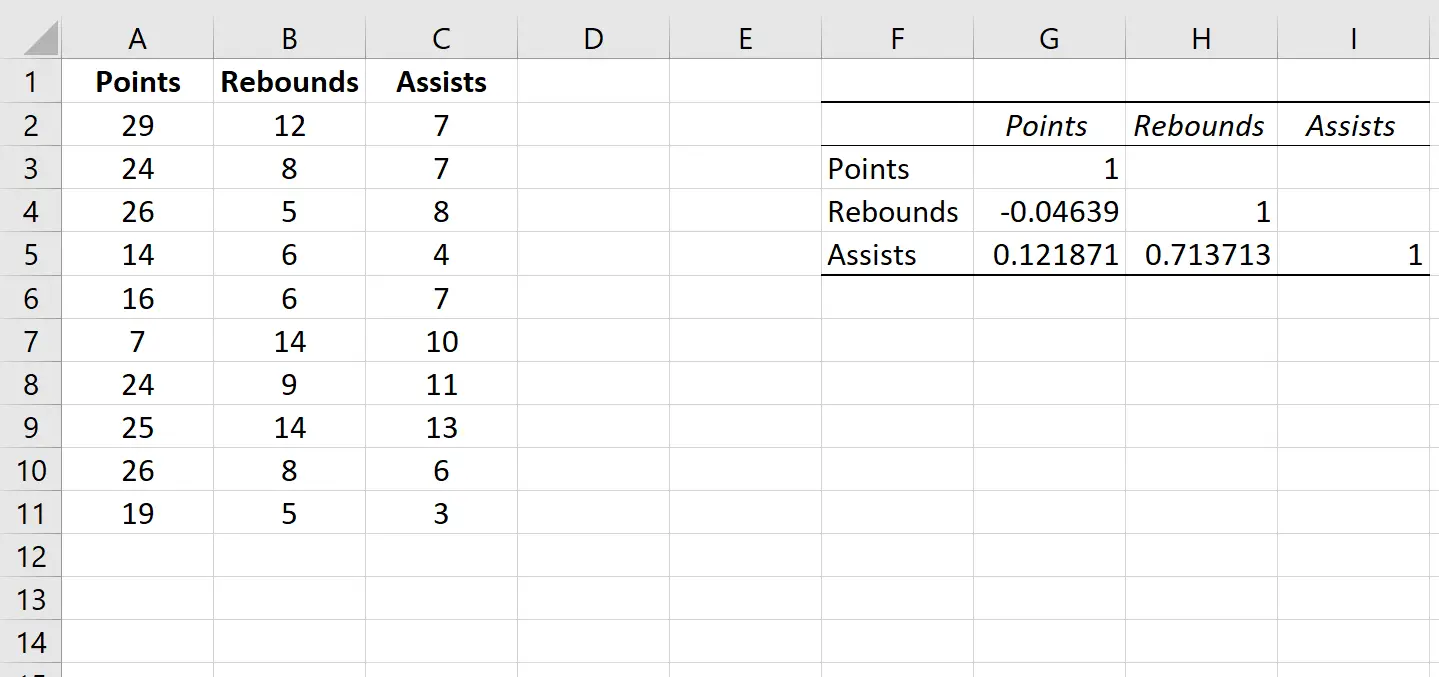
Excel’de bir korelasyon matrisi nasıl yorumlanır

Korelasyon matrisinin bireysel hücrelerindeki değerler bize değişkenlerin her ikili kombinasyonu arasındaki Pearson korelasyon katsayısını anlatır. Örneğin:

Sayılar ve ribauntlar arasındaki korelasyon: -0,04639. Sayılar ve ribaundlar arasında biraz negatif korelasyon var ancak bu değer sıfıra o kadar yakın ki bu iki değişken arasında anlamlı bir ilişki olduğuna dair güçlü bir kanıt yok.

Sayılar ve asistler arasındaki korelasyon: 0,121871. Sayılar ve asistler arasında hafif bir pozitif korelasyon var ancak bu değer de sıfıra oldukça yakın, dolayısıyla bu iki değişken arasında anlamlı bir ilişki olduğuna dair güçlü bir kanıt yok.

Ribaund ve asist arasındaki korelasyon: 0,713713. Ribaundlar ve asistler arasında güçlü bir pozitif korelasyon vardır. Yani daha fazla ribaund alan oyuncular aynı zamanda daha fazla asist yapma eğilimindedir.

Bir değişken ile kendisi arasındaki korelasyon her zaman 1 olduğundan korelasyon matrisinin köşegen değerlerinin hepsinin 1 olduğuna dikkat edin. Pratikte bu sayının yorumlanması yararlı değildir.

Bonus: Korelasyon katsayılarını görselleştirin

Tablodaki korelasyon katsayılarının değerini görselleştirmenin basit bir yolu, tabloya koşullu biçimlendirme uygulamaktır.

Excel’in üst şeridinde Giriş sekmesine ve ardından Stiller grubuna gidin.

Koşullu Biçimlendirme Tablosu’nu , ardından Renk Ölçekleri’ni ve ardından Yeşil-Sarı-Kırmızı Renk Ölçeği’ni tıklayın.

Bu, aşağıdaki renk ölçeğini otomatik olarak korelasyon matrisine uygular:

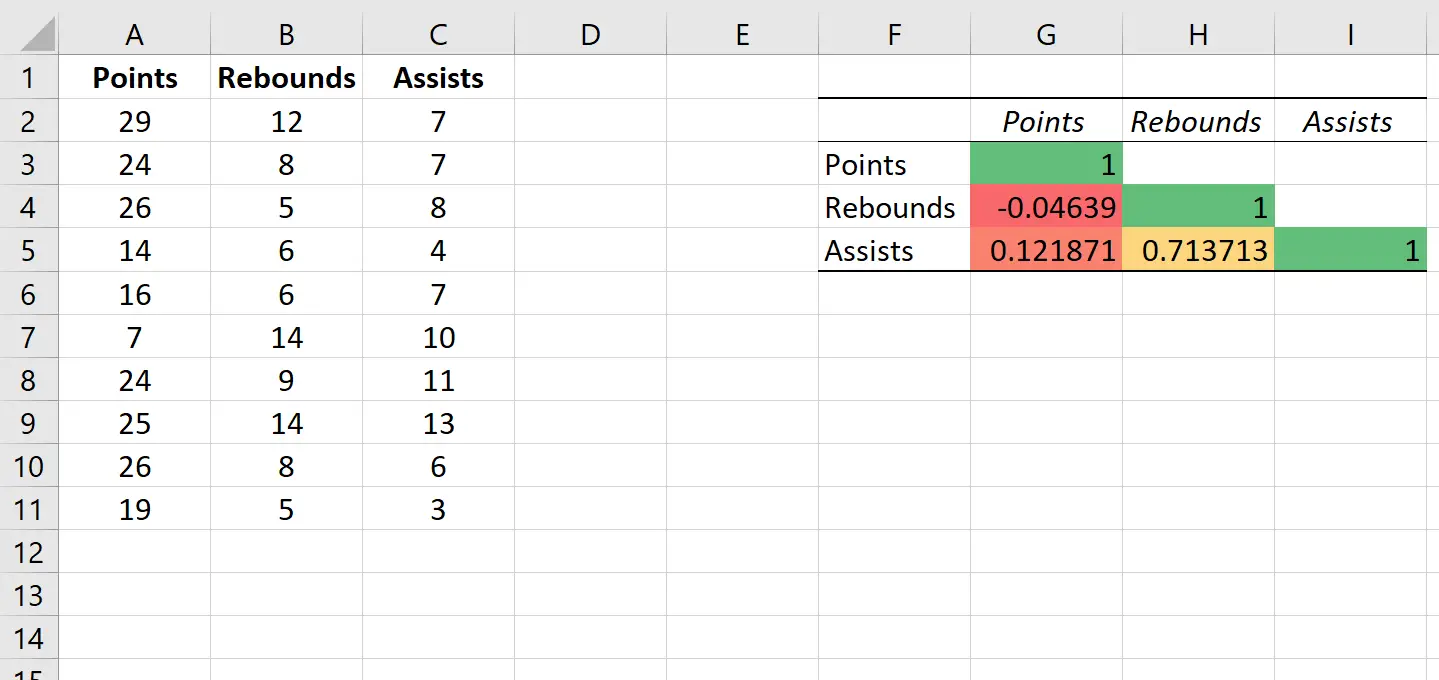
Bu, değişkenler arasındaki korelasyonun gücünü kolayca görselleştirmemize yardımcı olur.

Çok sayıda değişken içeren bir korelasyon matrisiyle çalışıyorsak bu özellikle yararlı bir ipucudur çünkü en güçlü korelasyonlara sahip değişkenleri hızlı bir şekilde belirlememize yardımcı olur.

İlgili: Ne “güçlü” bir korelasyon olarak kabul edilir?

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de Dağılım Grafiği Matrisi Nasıl Oluşturulur
Excel’de korelasyon testi nasıl yapılır