Excel'de vif nasıl hesaplanır

Regresyon analizinde çoklu bağlantı, iki veya daha fazla açıklayıcı değişkenin regresyon modelinde benzersiz veya bağımsız bilgi sağlamayacak şekilde birbiriyle yüksek düzeyde korelasyona sahip olması durumunda ortaya çıkar. Değişkenler arasındaki korelasyon derecesi yeterince yüksekse, bu durum regresyon modelinin yerleştirilmesinde ve yorumlanmasında sorunlara neden olabilir.

Neyse ki, bir regresyon modelinde açıklayıcı değişkenler arasındaki korelasyonu ve korelasyonun gücünü ölçen, varyans enflasyon faktörü (VIF) adı verilen bir ölçüm kullanarak çoklu doğrusallığı tespit etmek mümkündür.

Bu eğitimde Excel’de VIF’nin nasıl hesaplanacağı açıklanmaktadır.

Örnek: Excel’de VIF’nin hesaplanması

Bu örnek için, 10 basketbolcunun özelliklerini tanımlayan aşağıdaki veri kümesini kullanarak çoklu doğrusal regresyon gerçekleştireceğiz. Tepki değişkeni olarak reytingi ve açıklayıcı değişkenler olarak da sayılar, asistler ve ribaundları kullanarak bir regresyon modeli uygulayacağız. Daha sonra her açıklayıcı değişken için VIF değerlerini belirleyeceğiz.

Adım 1: Çoklu doğrusal regresyon gerçekleştirin.

Üst şeritte Veri sekmesine gidin ve Veri Analizi’ni tıklayın. Bu seçeneği görmüyorsanız, öncelikle ücretsiz Analysis ToolPak yazılımını yüklemelisiniz .

Veri Analizi’ne tıkladığınızda yeni bir pencere açılacaktır. Regresyon’u seçin ve Tamam’a tıklayın.

Yanıt değişkenleri ve açıklayıcı değişkenler için gerekli tabloları doldurun ve ardından Tamam’a tıklayın.

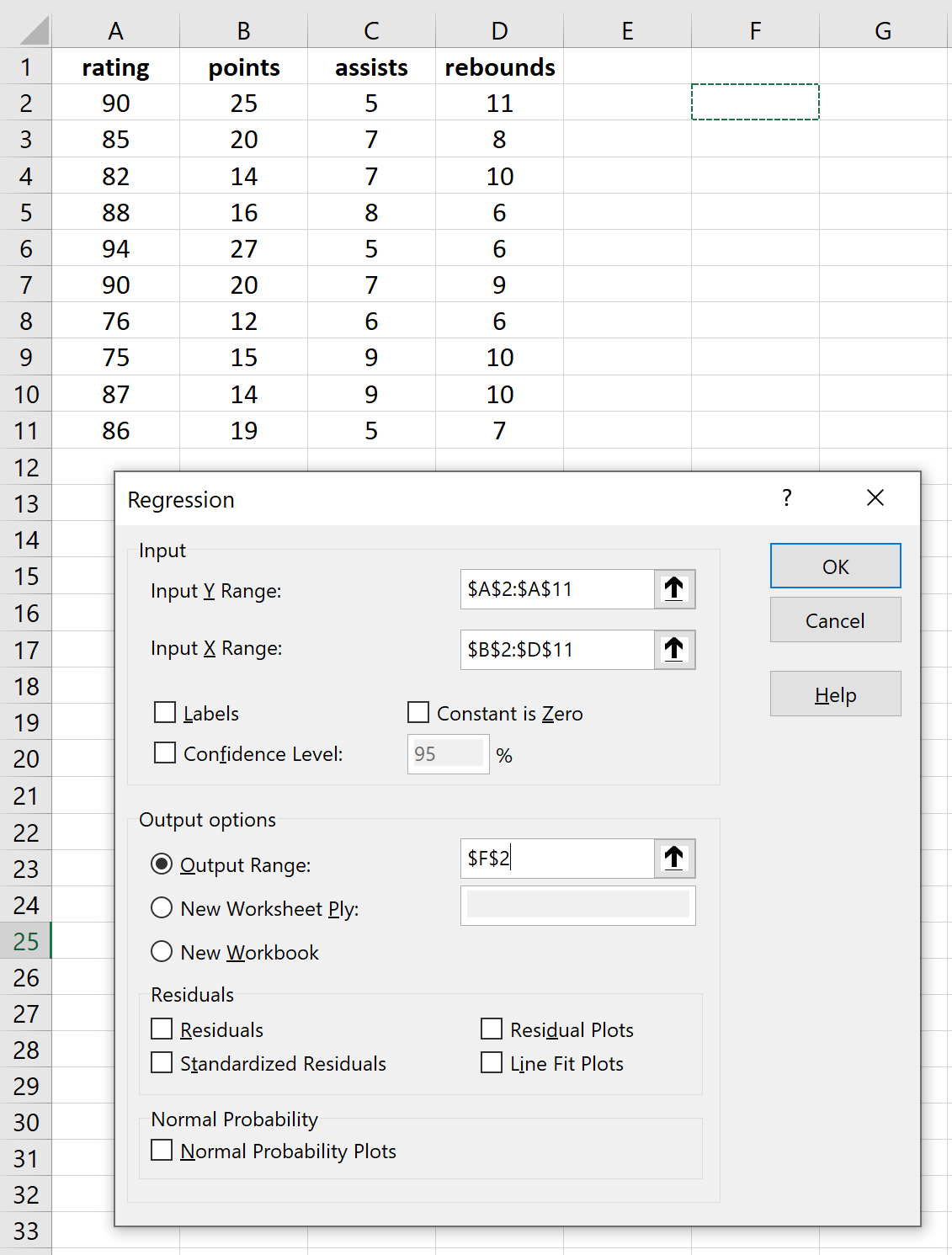
Bu, aşağıdaki sonucu üretir:

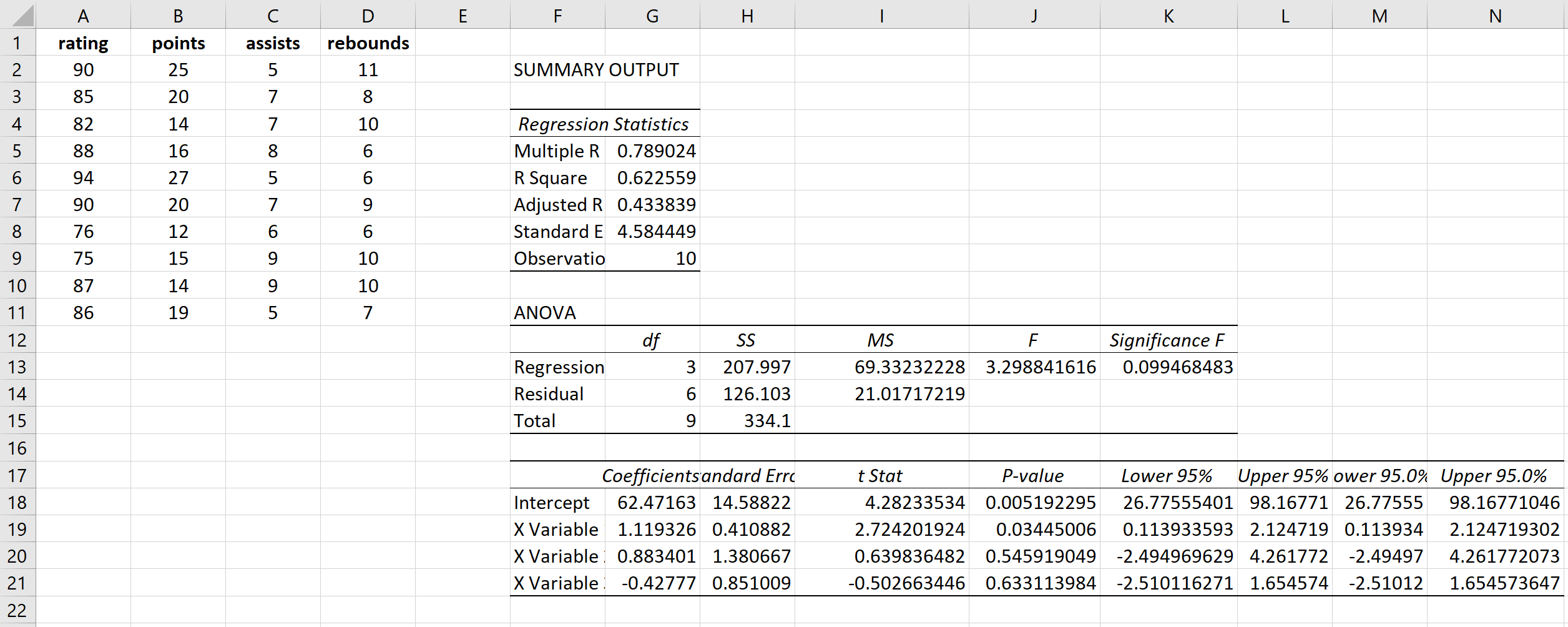
Adım 2: Her açıklayıcı değişken için VIF’yi hesaplayın.

Daha sonra, bir açıklayıcı değişkeni yanıt değişkeni ve diğer ikisini açıklayıcı değişken olarak kullanarak bireysel regresyonlar gerçekleştirerek üç açıklayıcı değişkenin her biri için VIF’yi hesaplayabiliriz.

Örneğin, puanları yanıt değişkeni olarak ve asistleri ve ribaundları açıklayıcı değişkenler olarak kullanarak çoklu doğrusal regresyon gerçekleştirerek puan değişkeni için VIF’yi hesaplayabiliriz.

Bu, aşağıdaki sonucu üretir:

Puanların VIF’si 1/(1 – R Kare) = 1/(1 – .433099) = 1,76 olarak hesaplanır.

Daha sonra bu işlemi diğer iki değişken olan asistler ve ribaundlar için tekrarlayabiliriz.

Üç açıklayıcı değişkenin VIF’lerinin aşağıdaki gibi olduğu ortaya çıktı:

puan: 1.76
asist: 1.96
ribaund: 1.18

VIF değerleri nasıl yorumlanır?

VIF değeri 1’den başlar ve üst sınırı yoktur. VIF’leri yorumlamanın genel kuralı şudur:

• 1 değeri, belirli bir açıklayıcı değişken ile modeldeki diğer herhangi bir açıklayıcı değişken arasında bir korelasyon olmadığını gösterir.
• 1 ile 5 arasındaki bir değer, belirli bir açıklayıcı değişken ile modeldeki diğer açıklayıcı değişkenler arasında orta düzeyde bir korelasyon olduğunu gösterir, ancak bu genellikle özel dikkat gerektirecek kadar şiddetli değildir.
• 5’ten büyük bir değer, belirli bir açıklayıcı değişken ile modeldeki diğer açıklayıcı değişkenler arasında potansiyel olarak ciddi bir korelasyon olduğunu gösterir. Bu durumda regresyon sonuçlarındaki katsayı tahminleri ve p değerleri muhtemelen güvenilmez olacaktır.

Regresyon modelimizde açıklayıcı değişkenlerin VIF değerlerinin her biri 1’e kapalı olduğundan örneğimizde çoklu doğrusallık sorun teşkil etmemektedir.