Excel'de p değerleri nasıl hesaplanır (3 örnek)

İstatistikte, bir popülasyon parametresi hakkındaki bir ifadenin doğru olup olmadığını belirlemek için hipotez testini kullanırız.

Bir hipotez testi uyguladığımızda genellikle bize bir T-puanı test istatistiği verilir.

Bu t-puanı test istatistiğini bulduğumuzda, onunla ilişkili p-değerini de bulabiliriz.

Eğer bu p değeri belirli bir değerden küçükse (örneğin 0,10, 0,05, 0,01), testin sıfır hipotezini reddeder ve sonuçlarımızın istatistiksel olarak anlamlı olduğu sonucuna varırız.

Aşağıdaki örnekler, Excel’de bir test istatistiği için p değerinin üç farklı senaryoda nasıl hesaplanacağını gösterir.

Örnek 1: İki kuyruklu bir test için P değerini hesaplayın

Bir botanikçinin belirli bir bitki türünün ortalama boyunun 15 inç olup olmadığını bilmek istediğini varsayalım.

12 bitkiden oluşan rastgele bir örnekte , örneğin ortalama yüksekliğinin 14,33 inç ve örneğin standart sapmasının 1,37 inç olduğunu bulur.

Aşağıdaki boş ve alternatif hipotezleri kullanarak bir hipotez testi gerçekleştirir:

H ₀ (sıfır hipotezi): μ= 15 inç

_HA (alternatif hipotez): μ ≠ 15 inç

Test istatistiği şu şekilde hesaplanır:

• t = ( X – µ) / (s/ √n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1,694

Bu test istatistiğiyle ilişkili serbestlik dereceleri n-1 = 12-1 = 11’dir .

Bu test istatistiğinin p değerini bulmak için Excel’de aşağıdaki formülü kullanacağız:

 =T.DIST.2T(ABS(-1.694), 11)

Aşağıdaki ekran görüntüsü bu formülün pratikte nasıl kullanılacağını göstermektedir.

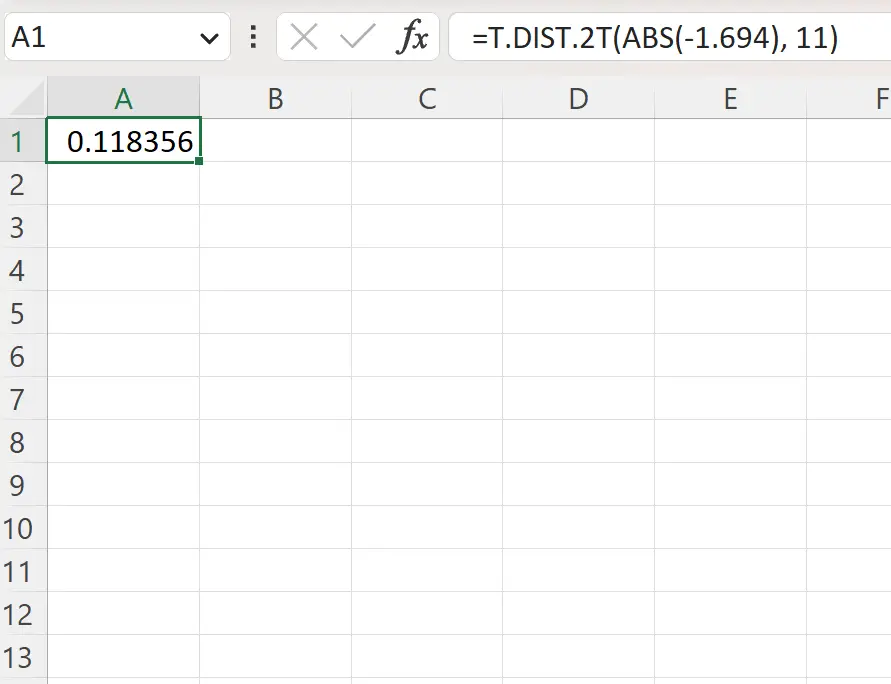
İki kuyruklu p değeri 0,1184’tür .

Bu değerden beri 0,05’ten küçük değilse sıfır hipotezini reddedemiyoruz. Ortalama bitki boyunun 15 inçten farklı olduğunu söyleyecek yeterli kanıtımız yok.

Örnek 2: Soldaki test için P değerini hesaplayın

Bir fabrikada üretilen belirli bir aletin ortalama ağırlığının 20 gram olduğunu varsayalım. Ancak bir müfettiş, gerçek ortalama ağırlığın 20 gramdan az olduğunu tahmin ediyor.

Bunu test etmek için 20 widget’tan oluşan basit rastgele bir örneği tartar ve aşağıdaki bilgileri alır:

• n = 20 widget
• x = 19,8 gram
• s = 3,1 gram

Daha sonra aşağıdaki boş ve alternatif hipotezleri kullanarak bir hipotez testi gerçekleştirir:

H ₀ (sıfır hipotezi): μ ≥ 20 gram

_HA (alternatif hipotez): μ < 20 gram

Test istatistiği şu şekilde hesaplanır:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -.2885

Bu test istatistiğiyle ilişkili serbestlik dereceleri n-1 = 20-1 = 19’dur .

Bu test istatistiğinin p değerini bulmak için Excel’de aşağıdaki formülü kullanacağız:

 =T.DIST(-.2885, 19, TRUE)

Aşağıdaki ekran görüntüsü bu formülün pratikte nasıl kullanılacağını göstermektedir.

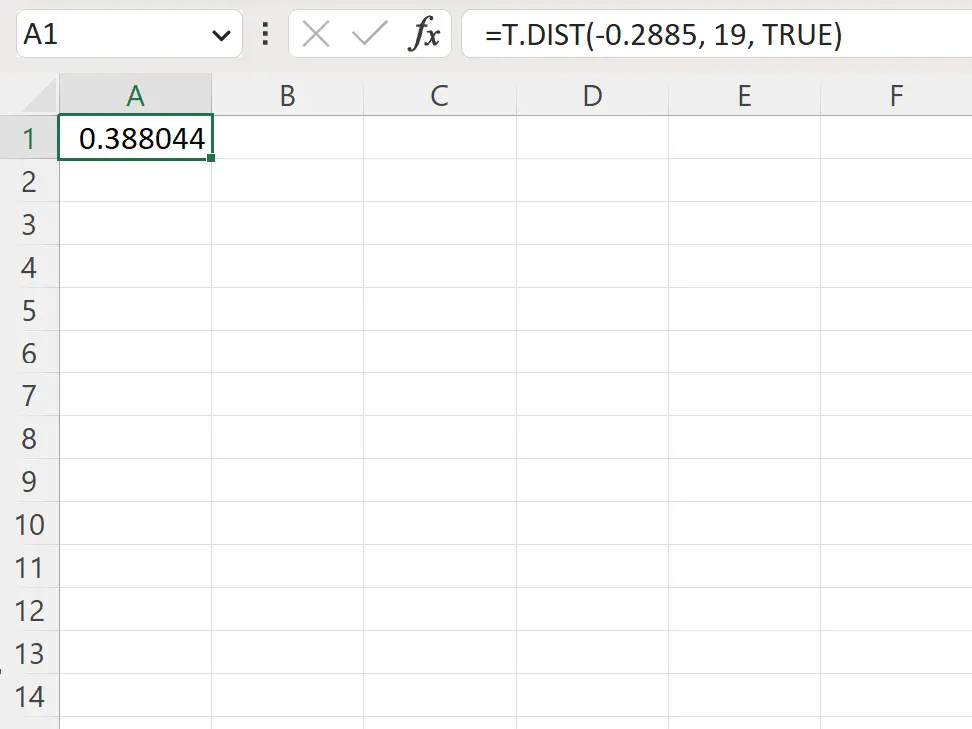
Soldaki p değeri 0,388044’tür .

Bu değerden beri 0,05’ten az değilse denetçi sıfır hipotezini reddetmede başarısız olur. Bu fabrikada üretilen aletlerin gerçek ortalama ağırlığının 20 gramdan az olduğunu söylemek için yeterli kanıt yok.

Not : p değeri hesaplanırken kümülatif dağılım fonksiyonunun kullanılması gerektiğini belirtmek için TRUE argümanını kullandık.

Örnek 3: Sağ kuyruklu test için P değerini hesaplayın

Belirli bir bitki türünün ortalama boyunun 10 inç olduğunu varsayalım. Ancak bir botanikçi, gerçek ortalama yüksekliğin 10 inçten fazla olduğunu söylüyor.

Bu iddiayı test etmek için 15 bitkiden oluşan basit rastgele bir örneğin yüksekliğini ölçer ve aşağıdaki bilgileri elde eder:

• n = 15 bitki
• x = 11,4 inç
• s = 2,5 inç

Daha sonra aşağıdaki boş ve alternatif hipotezleri kullanarak bir hipotez testi gerçekleştirir:

H ₀ (sıfır hipotezi): μ ≤ 10 inç

_HA (alternatif hipotez): μ > 10 inç

Test istatistiği şu şekilde hesaplanır:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

Bu test istatistiğiyle ilişkili serbestlik dereceleri n-1 = 15-1 = 14’tür .

Bu test istatistiğinin p değerini bulmak için Excel’de aşağıdaki formülü kullanacağız:

 =T.DIST.RT(2.1689, 14)

Aşağıdaki ekran görüntüsü bu formülün pratikte nasıl kullanılacağını göstermektedir.

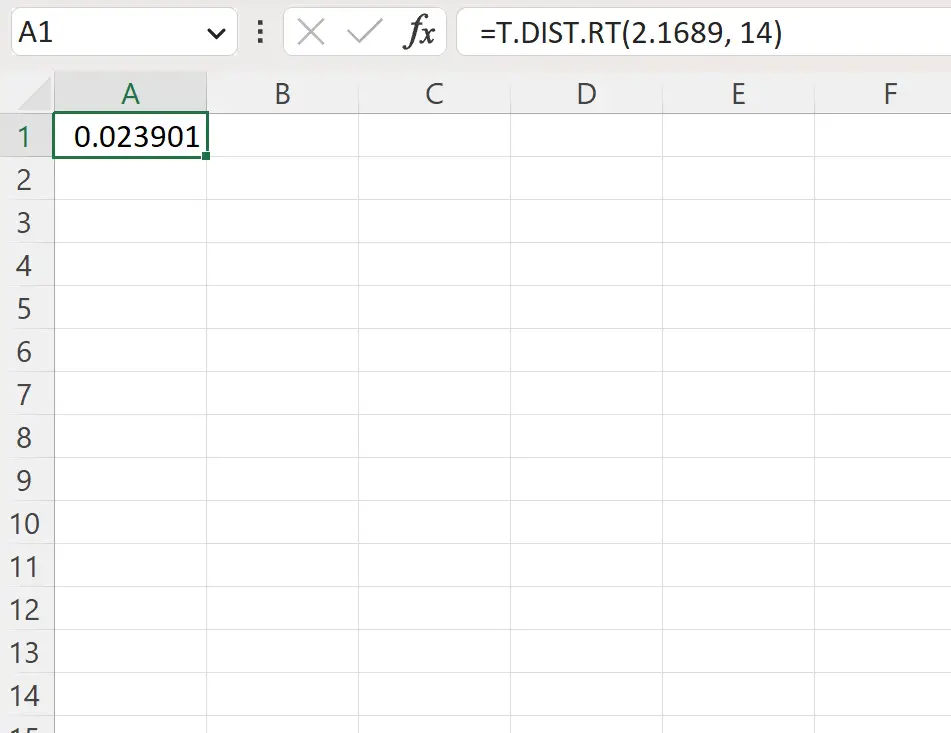
Sağdaki p değeri 0,023901’dir .

Bu değer 0,05’ten küçük olduğundan botanikçi sıfır hipotezini reddedebilir. Bu bitki türünün gerçek ortalama boyunun 10 inçten fazla olduğunu söyleyecek yeterli kanıtı var.

Ek kaynaklar

Aşağıdaki eğitimlerde Excel’deki diğer genel görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de Z Puanından P Değeri Nasıl Bulunur?
Excel’de bir F istatistiğinin P değeri nasıl bulunur?
Excel’de ki-kare istatistiğinin P değeri nasıl bulunur?