Excel: regresyon katsayısı için güven aralığını hesaplayın

Doğrusal bir regresyon modelinde, bir regresyon katsayısı bize yordayıcı değişkendeki bir birimlik artışla ilişkili yanıt değişkenindeki ortalama değişikliği anlatır.

Bir regresyon katsayısına ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanabiliriz:

β ₁ için güven aralığı : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

Altın:

•   b ₁ = Regresyon tablosunda gösterilen regresyon katsayısı
• t _{1-∝/2, n-2} = n-2 serbestlik derecesine sahip 1-∝ güven düzeyi için kritik t değeri; burada n , veri setimizdeki toplam gözlem sayısıdır
• se(b ₁ ) = Regresyon tablosunda gösterilen b _1’in standart hatası

Aşağıdaki örnek, Excel’de bir regresyon katsayısı için güven aralığının nasıl hesaplanacağını gösterir.

Örnek: Excel’de Regresyon Katsayısı için Güven Aralığı

Belirli bir sınıftaki 15 öğrenci için yordayıcı değişken olarak çalışılan saatleri ve yanıt değişkeni olarak sınav puanlarını kullanarak basit bir doğrusal regresyon modeli uydurmak istediğimizi varsayalım:

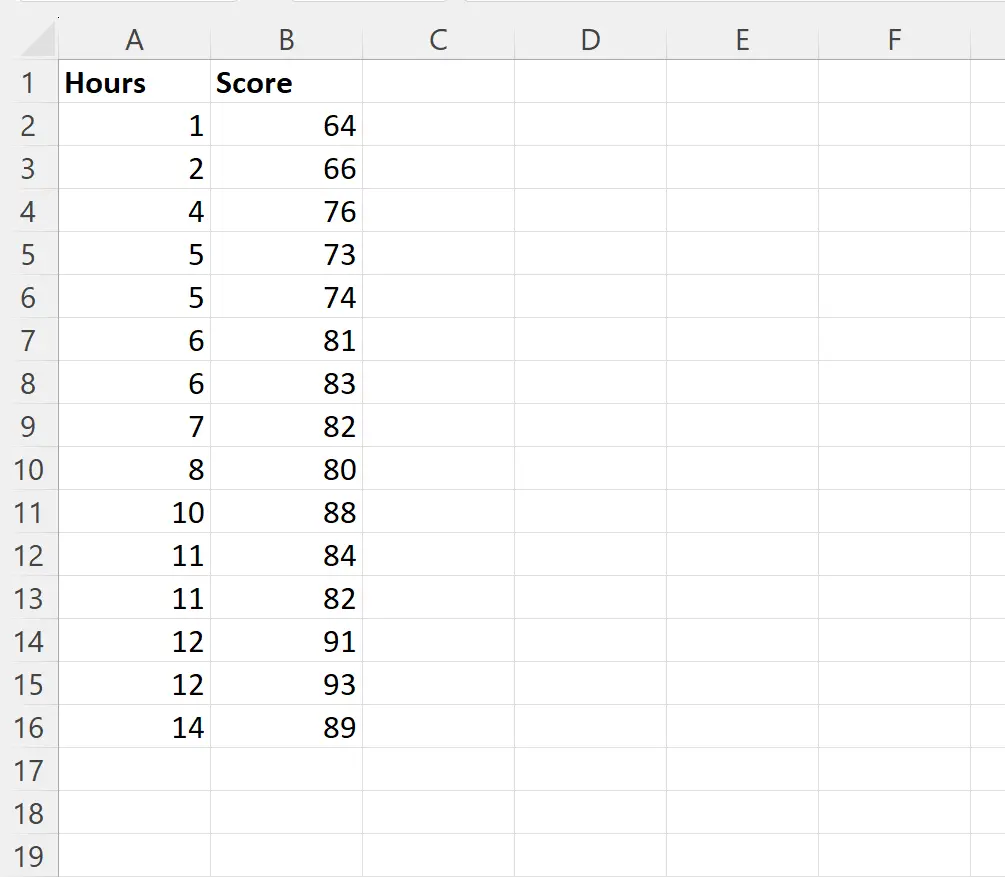
Saat sütunundaki değerleri yordayıcı değişken olarak ve Puan sütunundaki değerleri yanıt değişkeni olarak kullanarak basit bir doğrusal regresyon gerçekleştirmek için D2 hücresine aşağıdaki formülü yazabiliriz:

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

İlk DOĞRU bağımsız değişkeninin Excel’e, regresyon denkleminin kesişim noktasını sıfır olmaya zorlamadan normal şekilde hesaplamasını söylediğini unutmayın.

İkinci DOĞRU bağımsız değişkeni, Excel’e katsayılara ek olarak ek regresyon istatistikleri üretmesini söyler.

Aşağıdaki ekran görüntüsü bu formülün sonucunu göstermektedir (çıktının altındaki kırmızı metinde her bir çıktı değerinin neyi temsil ettiğini açıklıyoruz):

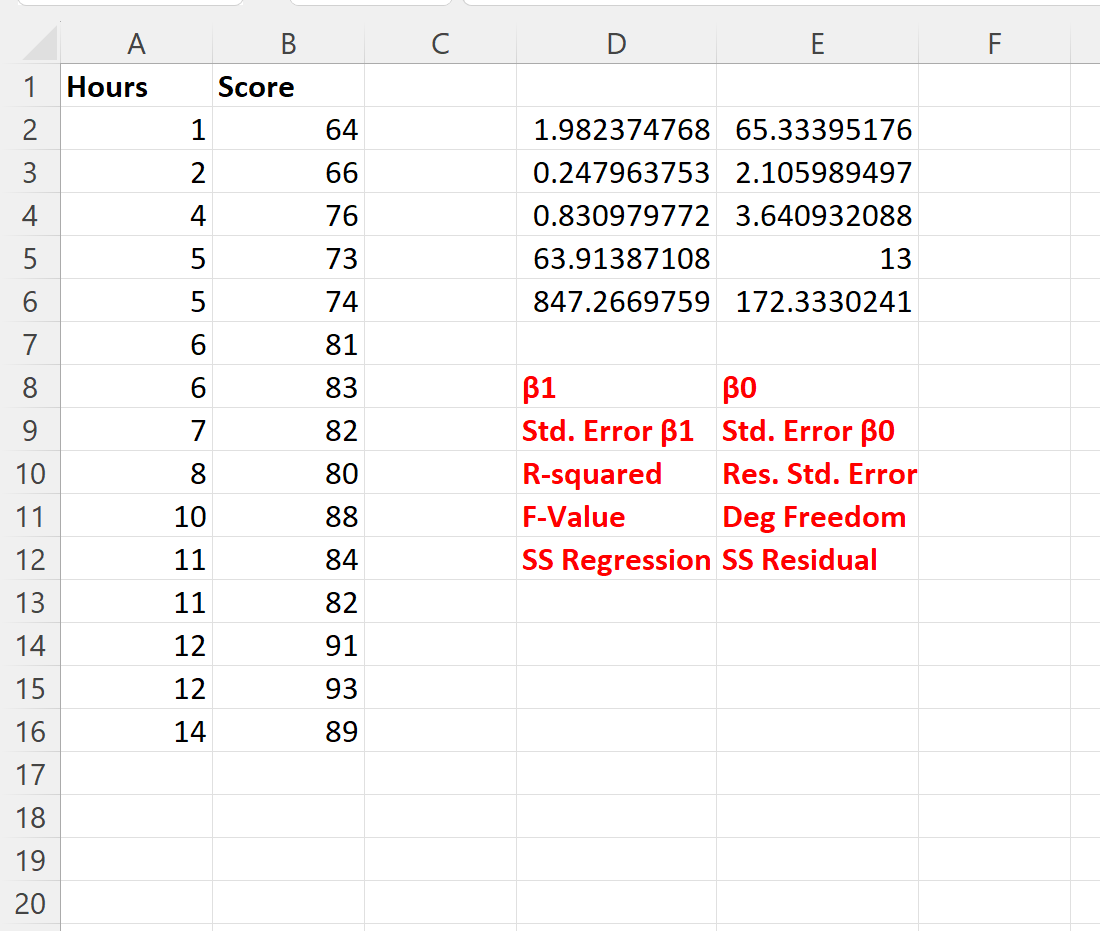
Regresyon katsayılarını kullanarak uygun regresyon denklemini aşağıdaki gibi yazabiliriz:

Puan = 65.334 + 1.982*(Çalışma saati)

Saatlere ilişkin regresyon katsayısının 1,982 olduğunu unutmayın.

Bu bize, harcanan her ek çalışma saatinin sınav puanında ortalama 1.982 puanlık bir artışla ilişkili olduğunu söylüyor.

Regresyon katsayısı için %95 güven aralığını hesaplamak amacıyla H2 ve H3 hücrelerine aşağıdaki formülleri girebiliriz:

• H2: = D2 – T.TERS.2T(0,05; E5)*D3
• H3: = D2 + T.TERS.2T(0,05; E5)*D3

Aşağıdaki ekran görüntüsü bu formüllerin pratikte nasıl kullanılacağını göstermektedir:

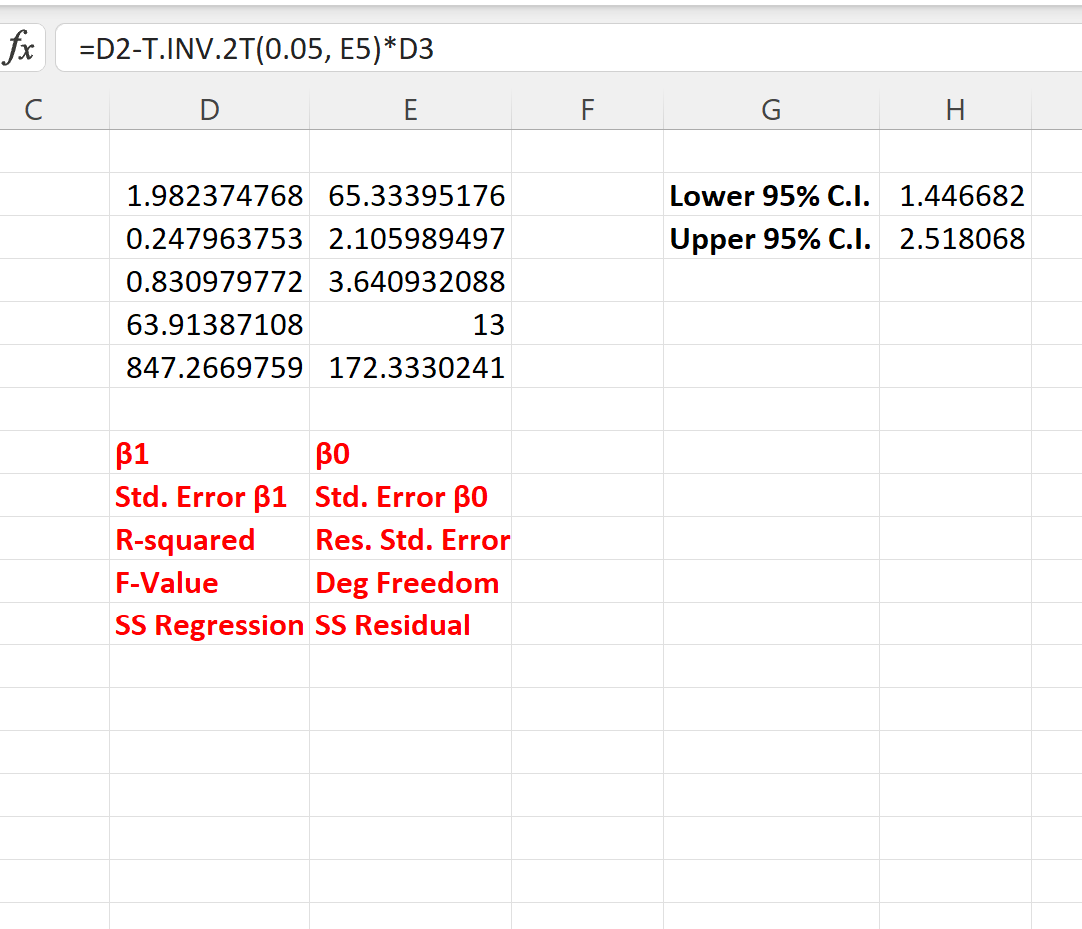
Regresyon katsayısı için %95 güven aralığı [1,446, 2,518]’ dir.

Bu güven aralığı 0 değerini içermediğinden çalışılan saat ile sınav notu arasında istatistiksel olarak anlamlı bir ilişkinin olduğu sonucuna varabiliriz.

Regresyon katsayısı için %95 güven aralığını manuel olarak hesaplayarak da bunun doğru olduğunu doğrulayabiliriz:

• β ₁ için %95 GA: b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• β ₁ için %95 GA: 1,982 ± t _{0,975, 15-2} * 0,248
• β ₁ için %95 GA: 1,982 ± 2,1604 * 0,248
• β ₁ için %95 GA: [1,446, 2,518]

Regresyon katsayısı için %95 güven aralığı [1,446, 2,518]’ dir.

Ek kaynaklar

Aşağıdaki eğitimlerde Excel’deki diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de basit doğrusal regresyon nasıl gerçekleştirilir
Excel’de çoklu doğrusal regresyon nasıl gerçekleştirilir
Excel’de regresyon çıktısında P değerleri nasıl yorumlanır