Faktöriyel anova nedir? (tanım & #038; örnek)

Faktöriyel ANOVA, iki veya daha fazla bağımsız faktör ve tek bir yanıt değişkeni kullanan herhangi bir ANOVA’dır (“varyans analizi”).

Bu tür ANOVA, iki veya daha fazla faktörün bir yanıt değişkenini nasıl etkilediğini ve faktörler arasında yanıt değişkeni üzerinde bir etkileşim etkisinin olup olmadığını anlamak istediğinizde kullanılmalıdır.

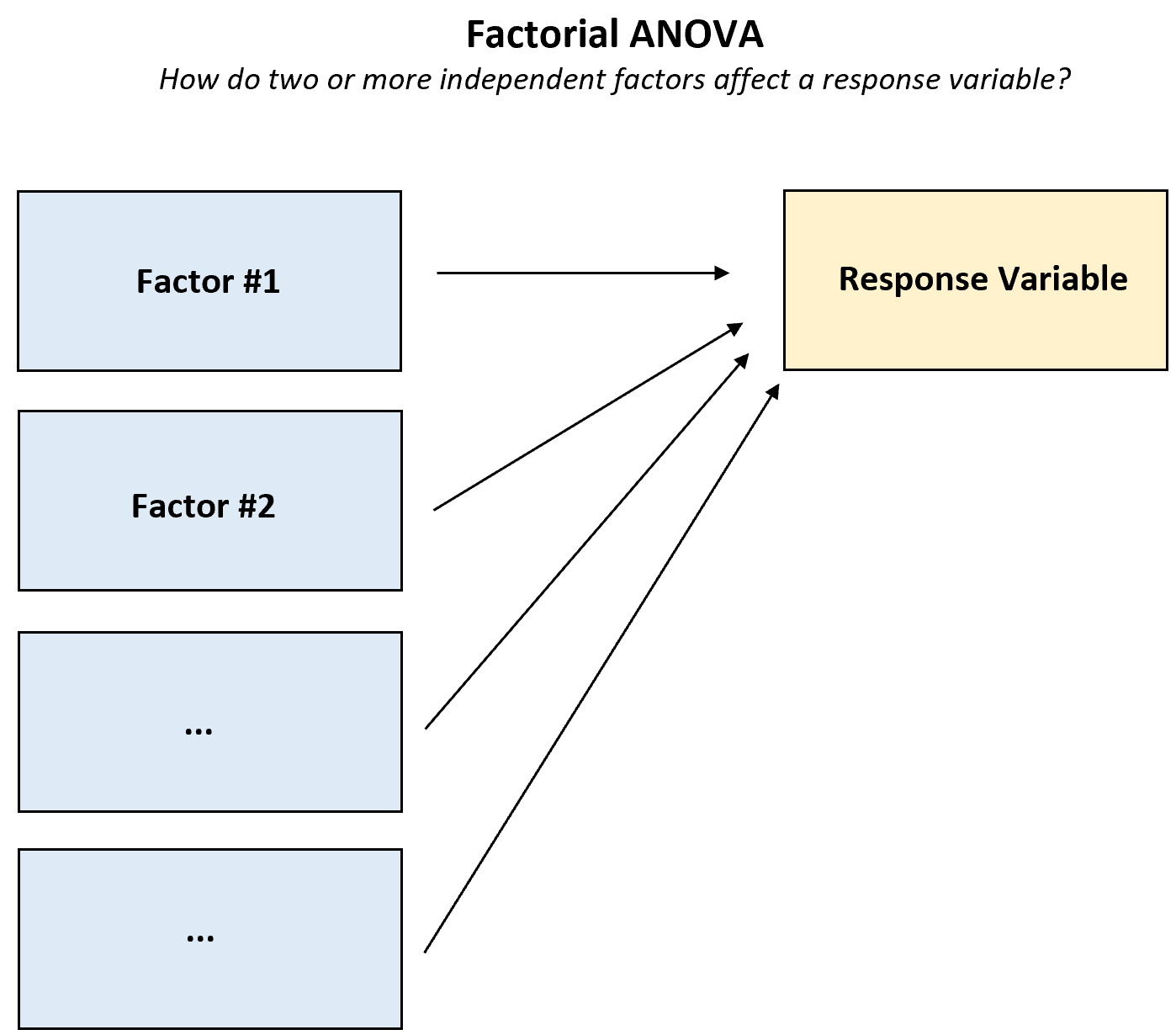
Bu eğitimde faktöriyel ANOVA’nın kullanılabileceği durumların çeşitli örneklerinin yanı sıra faktöriyel ANOVA’nın nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

Not: İki yönlü ANOVA, faktöriyel ANOVA’nın bir türüdür.

Faktöriyel ANOVA kullanma örnekleri

Faktöriyel ANOVA aşağıdaki durumların her birinde kullanılabilir.

Örnek 1: Bitki Büyümesi

Bir botanikçi güneşe maruz kalmanın ve sulama sıklığının bitki büyümesini nasıl etkilediğini anlamak ister. 100 tohum ekiyor ve bunların değişen güneş ışığı koşulları ve sulama sıklığı altında üç ay boyunca büyümelerine izin veriyor. Üç ay sonra her bitkinin yüksekliğini kaydediyor.

Bu durumda aşağıdaki değişkenlere sahiptir:

• Tepki değişkeni: bitki büyümesi
• Faktörler: güneşe maruz kalma, sulama sıklığı

Ve şu sorulara yanıt vermek istiyor:

• Güneşe maruz kalmak bitki büyümesini etkiler mi?
• Sulama sıklığı bitki büyümesini etkiler mi?
• Güneşe maruz kalma ile sulama sıklığı arasında bir etkileşim etkisi var mı?

İki faktörün tek bir yanıt değişkenini nasıl etkilediğini anlamak istediği için bu analiz için faktöriyel ANOVA kullanabilir.

Örnek 2: Sınav sonuçları

Bir profesör ders saatinin ve öğretim yönteminin sınav sonuçlarını nasıl etkilediğini anlamak istiyor. İki farklı öğretim yöntemi ve iki farklı öğretim saati (sabah erken ve öğleden sonra) kullanır ve her öğrencinin dönem sonundaki ortalama sınav puanlarını kaydeder.

Bu durumda aşağıdaki değişkenlere sahiptir:

• Yanıt değişkeni: sınav puanı
• Faktörler: öğretim yöntemi, öğretim süresi

Ve şu sorulara yanıt vermek istiyor:

• Öğretim yöntemi sınav sonuçlarını etkiler mi?
• Ders verme süresi sınav puanlarını etkiler mi?
• Öğretim yöntemi ile öğretim süresi arasında etkileşim etkisi var mıdır?

İki faktörün tek bir yanıt değişkenini nasıl etkilediğini anlamak istediği için bu analiz için faktöriyel ANOVA kullanabilir.

Örnek 3: Yıllık gelir

Bir ekonomist, eğitim düzeyinin (lise diploması, üniversite diploması, yüksek lisans), medeni durumun (bekar, boşanmış, evli) ve bölgenin (Kuzey, Doğu, Güney, Batı) yıllık geliri nasıl etkilediğini anlamak için veri toplar.

Bu durumda aşağıdaki değişkenlere sahiptir:

• Yanıt değişkeni: yıllık gelir
• Faktörler: eğitim düzeyi, medeni durum, bölge

Ve şu sorulara yanıt vermek istiyor:

• Eğitim düzeyi geliri etkiler mi?
• Medeni durum geliri etkiler mi?
• Bölge geliri etkiler mi?
• Bu üç bağımsız faktör arasında etkileşim etkisi var mı?

Üç faktörün tek bir yanıt değişkenini nasıl etkilediğini anlamak istediği için bu analiz için faktöriyel ANOVA kullanabilir.

Faktöriyel ANOVA’nın adım adım örneği

Bir botanikçi güneş ışığına maruz kalmanın ve sulama sıklığının bitki büyümesini etkileyip etkilemediğini bilmek ister. 40 tohum ekiyor ve iki ay boyunca farklı güneş ışığı koşullarında ve sulama sıklığında büyümelerini sağlıyor. İki ay sonra her bitkinin yüksekliğini kaydediyor.

Sonuçlar aşağıda gösterilmektedir:

Her koşul kombinasyonunda beş bitkinin yetiştirildiğini görebiliriz.

Örneğin, beş bitki günlük sulamayla ve güneş ışığı olmadan büyütüldü ve iki ay sonra boyları 4,8 inç, 4,4 inç, 3,2 inç, 3,9 inç ve 4,4 inç oldu:

Botanikçi bu verileri Excel’de faktöriyel bir ANOVA gerçekleştirmek için kullanır ve aşağıdaki sonucu elde eder:

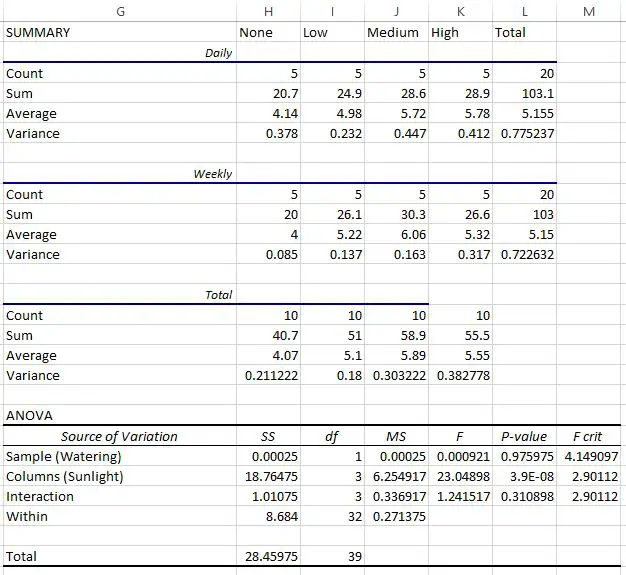
Son tablo faktöriyel ANOVA’nın sonucunu göstermektedir:

• Sulama sıklığı ile güneşe maruz kalma arasındaki etkileşimin p değeri 0,310898 idi. Bu durum 0,05 alfa düzeyinde istatistiksel olarak anlamlı değildir.
• Sulama sıklığına ilişkin p değeri 0,975975’tir . Bu durum 0,05 alfa düzeyinde istatistiksel olarak anlamlı değildir.
• Güneşe maruz kalmanın p değeri 3,9E-8 (0,000000039) idi. Bu, 0,05 alfa seviyesinde istatistiksel olarak anlamlıdır.

Güneş ışığına maruz kalmanın bitki büyümesi üzerinde istatistiksel olarak anlamlı etkiye sahip tek faktör olduğu sonucuna varabiliriz.

Ayrıca güneşe maruz kalma ile sulama sıklığı arasında herhangi bir etkileşim etkisinin olmadığı ve sulama sıklığının bitki büyümesi üzerinde istatistiksel olarak anlamlı bir etkisinin olmadığı sonucuna varabiliriz. bitkiler.

Ek kaynaklar

Aşağıdaki eğitimler ANOVA modelleri hakkında ek bilgi sağlar:

Tek Yönlü ANOVA’ya Giriş
İki Yönlü ANOVA’ya Giriş
Tekrarlanan Ölçümlere Giriş ANOVA
ANOVA, ANCOVA, MANOVA ve MANCOVA arasındaki farklar