Frekans dağılımı

Bu makalede frekans dağılımlarının ne olduğu ve nasıl elde edildiği açıklanmaktadır. Ayrıca frekans dağılımlarının adım adım örneklerini bulacaksınız ve ayrıca çözümlü alıştırmalarla pratik yapabileceksiniz.

Frekans dağılımı nedir?

İstatistikte frekans dağılımı , bir numunenin farklı değerlerinin satırlar halinde gruplandırıldığı ve her sütunda, her değerin frekans tipinin görüntülendiği bir tablodur. Bu nedenle bir veri setindeki tüm frekans türlerini göstermek için frekans dağılımı kullanılır.

Daha spesifik olarak, bir frekans dağılımı mutlak frekansı, kümülatif mutlak frekansı, bağıl frekansı ve kümülatif bağıl frekansı içerir.

Frekans dağılımlarının özelliklerinden biri, niceliksel bir değişken ve niteliksel bir değişkenin istatistiksel örneğini özetlemek için çok yararlı olmalarıdır.

Frekans dağılımı nasıl yapılır?

Frekans dağılımı gerçekleştirmek için aşağıdaki adımları izlemelisiniz:

1. Verileri farklı kategoriler halinde düzenleyin ve her satırın bir kategoriye karşılık geldiği bir tablo oluşturun.
2. Tablonun ikinci sütununda her kategorinin mutlak sıklığını hesaplayın.
3. Tablonun üçüncü sütununda her kategorinin kümülatif mutlak frekansını hesaplayın.
4. Tablonun dördüncü sütununda her kategorinin göreceli sıklığını hesaplayın.
5. Tablonun beşinci sütununda her kategorinin kümülatif bağıl sıklığını hesaplayın.
6. İsteğe bağlı olarak, göreceli frekansın ve kümülatif göreceli frekansın yüzde olarak hesaplandığı iki sütun eklenebilir, bunun için her iki sütunu da 100 ile çarpmanız yeterlidir.

Frekans dağılımı örneği

Frekans dağılımının tanımını ve nasıl oluşturulduğuna dair teoriyi gördükten sonra bu bölümde bir örnek adım adım çözülecektir.

• 30 kişilik bir sınıfta istatistik konusunda alınan notlar aşağıdaki gibidir. Veri kümesinin frekans dağılımını oluşturun.

Tüm sayılar yalnızca tam sayı olabildiği için ayrık bir değişkendir. Bu nedenle verileri aralıklar halinde gruplamak gerekli değildir.

Yani frekans dağılımı yapabilmek için her farklı değerin bir satır olacağı bir tablo oluşturmamız ve ardından her değerin mutlak frekansını bulmamız gerekiyor:

Tüm mutlak frekansların toplamının toplam veri sayısına eşit olduğunu unutmayın. Bu kurala uyulmaması, belirli bilgileri sağlamayı unuttuğunuz anlamına gelir.

Artık mutlak frekansı bildiğimize göre kümülatif mutlak frekansı hesaplamamız gerekiyor. Bu hesaplama için iki seçeneğimiz var: ya değerin mutlak frekansı artı en küçük değerlerin tüm mutlak frekanslarını toplarız ya da tam tersine, değerin mutlak frekansı artı önceki değerin kümülatif mutlak frekansını ekleriz.

Son değerin kümülatif mutlak frekansı her zaman toplam veri sayısına karşılık gelir; hesaplamaların doğru olduğunu doğrulamak için bu numarayı kullanabilirsiniz.

Daha sonra, mutlak frekansı toplam veri noktası sayısına (30) bölerek hesaplanan göreceli frekansı belirlememiz gerekir:

Tüm bağıl frekansların toplamının her zaman 1’e eşit olduğunu unutmayın; aksi takdirde bu, frekans dağılımının belirli bir hesaplamasının yanlış olduğu anlamına gelir.

Son olarak, kümülatif bağıl frekansı çıkarmamız gerekiyor. Bunu yapmak için, söz konusu değerin göreceli frekansını artı tüm önceki göreceli frekansları veya aynı anlama gelen önceki birikmiş göreceli frekansı eklemelisiniz:

Kısaca problem verisinin tüm frekansları ile frekans dağılımı şu şekildedir:

Gruplandırılmış veriler için frekans dağılımı

Aralıklar halinde gruplandırılmış veriler için bir frekans dağılımı yapmak için tek fark, veri kümesinin önce farklı aralıklar halinde gruplandırılmasının gerekmesidir, ancak hesaplamaların geri kalanı, frekans dağılımında olduğu gibi, veriler gruplandırılmadan aynı şekilde yapılır.

Örnek olarak, gruplandırılmış veriler için frekans dağılımı oluşturma problemi aşağıda çözülmüştür.

• 20 kişinin boyu ölçüldü ve aşağıda belirtilen sonuçlar elde edildi. Verileri aralıklara ayırarak frekans dağılımı oluşturun.

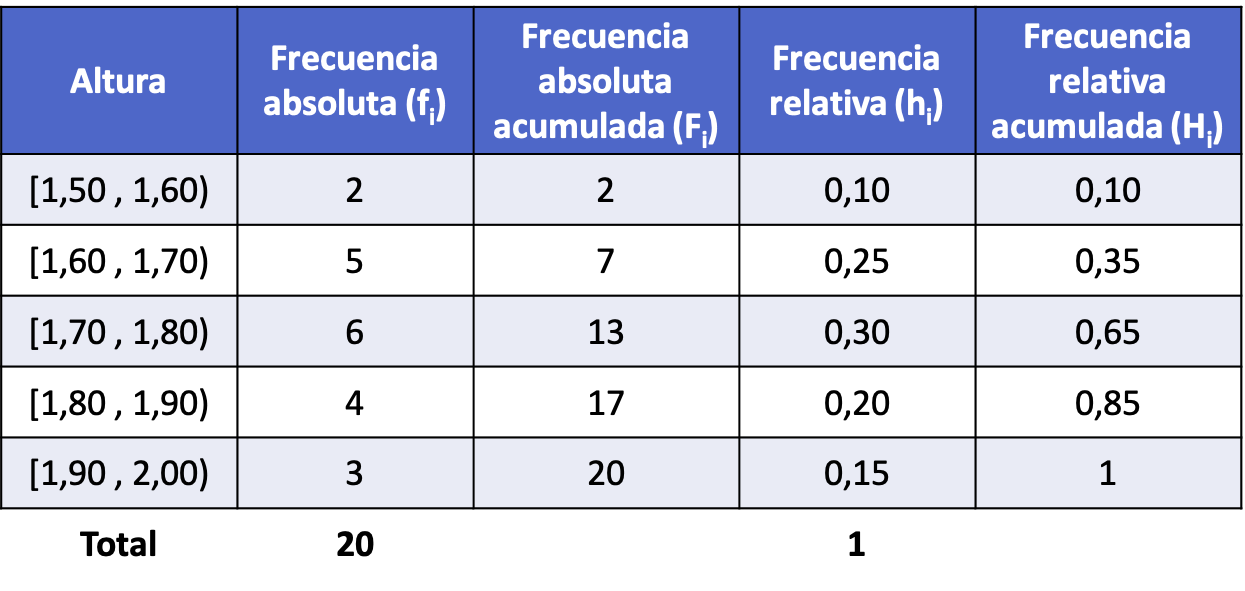
Bu örnekteki veriler, sayılar ondalık sayı olabileceğinden ve dolayısıyla herhangi bir değeri alabileceğinden sürekli bir dağılım izler. Bu nedenle verileri aralıklara göre gruplandırarak frekans dağılımını yapacağız.

Bir örneğin aralıklarını oluşturmak için çeşitli matematiksel kurallar olmasına rağmen, bu durumda sadece onda 10 genişliğinde aralıklar oluşturacağız.

Böylece, her aralık için tüm frekans türleri hesaplandıktan sonra (prosedür yukarıdaki örnektekiyle aynıdır), aralıklara göre gruplandırılmış verilerle frekans dağılımı şu şekilde olur:

Çözülmüş frekans dağılımı alıştırmaları

1. Egzersiz

20 kişiye ayda kaç kez sinemaya gittiklerini sorduk ve işte sonuçlar:

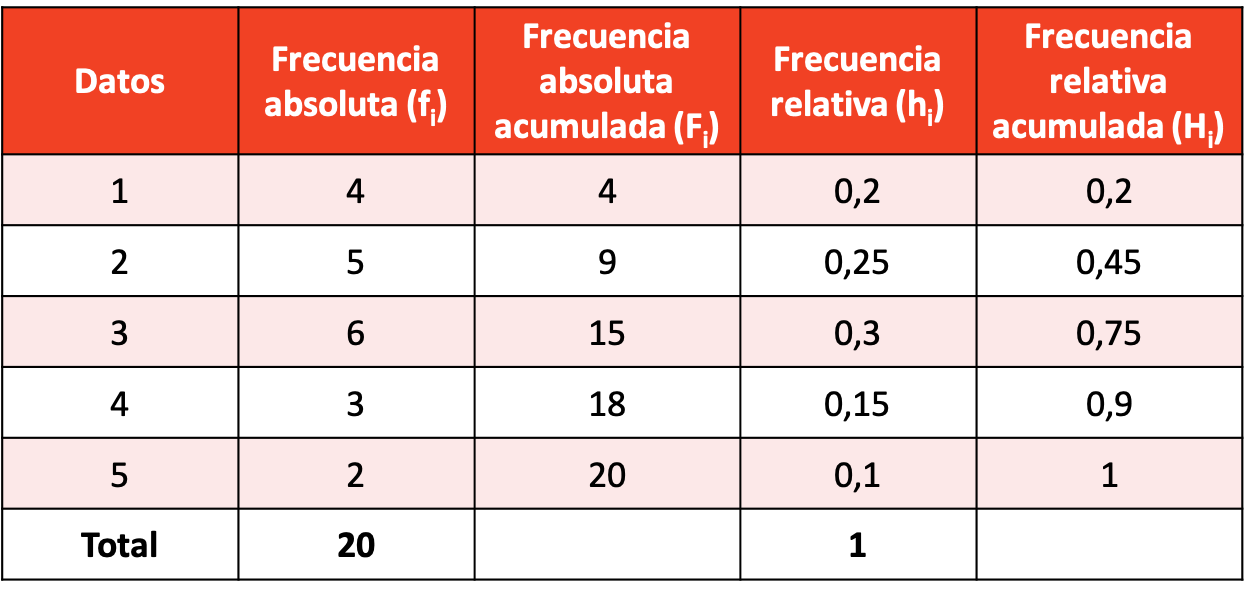
Ortaya çıkan veri örneğiyle bir frekans dağılımı yapın.

Tüm frekans türlerinin hesaplamaları ile frekans dağılımı aşağıdaki gibidir:

Alıştırma 2

36 çalışanı olan bir firmada çalışanların ağırlığına ilişkin istatistiksel bir çalışma yapmak istiyorsunuz. İşte işçilerin kilogram cinsinden ağırlıkları:

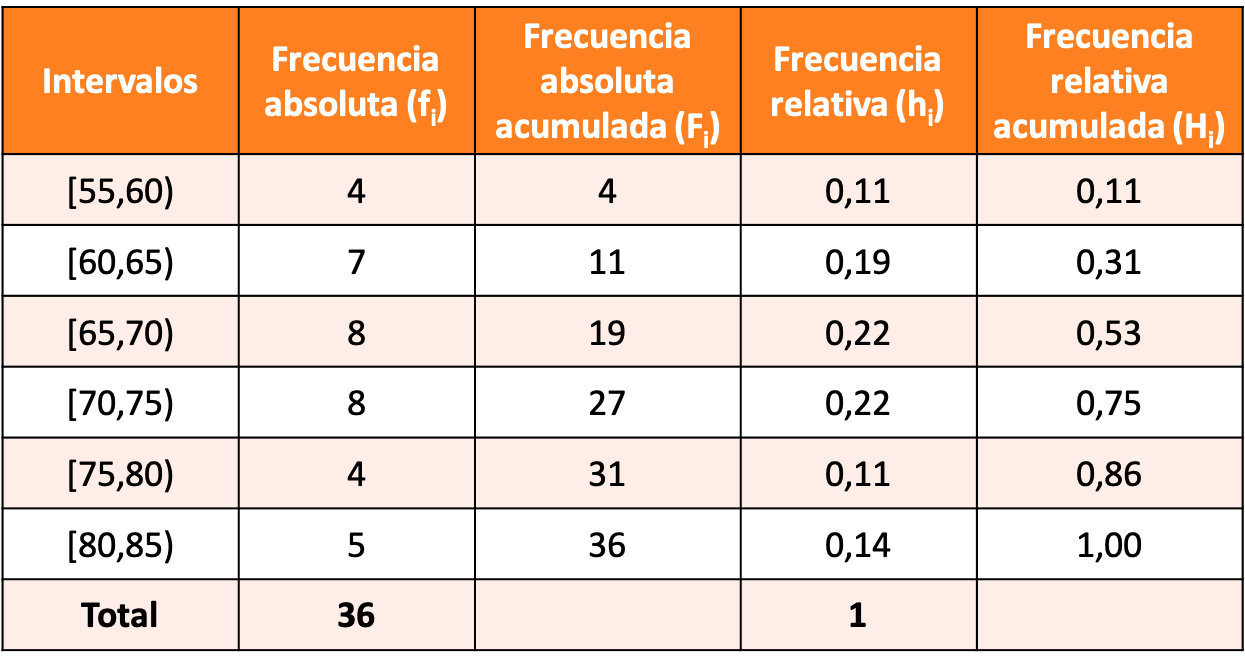
Gruplandırılmış verilerle 5 birim aralıklarla frekans dağılımı oluşturun ve ilk aralık [55,60] olsun.

Alıştırmanın çözümü aşağıdaki frekans dağılımıdır: