Gama dağılımı

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makalede gama dağılımının ne olduğu ve ne için kullanıldığı açıklanmaktadır. Böylece gama dağılımının tanımını, özelliklerini ve grafik gösteriminin nasıl göründüğünü bulacaksınız.

Gama dağılımı nedir?

Gama dağılımı, iki karakteristik parametre olan α ve λ ile tanımlanan sürekli bir olasılık dağılımıdır. Başka bir deyişle, gama dağılımı iki parametresinin değerine bağlıdır: α şekil parametresidir ve λ ölçek parametresidir.

Gama dağılımının sembolü büyük Yunan harfi Γ’dir. Yani bir rastgele değişken gama dağılımını takip ediyorsa şu şekilde yazılır:

$X\sim \Gamma(\alpha,\lambda)$

Gama dağılımı ayrıca şekil parametresi k = α ve ters ölçek parametresi θ = 1/λ kullanılarak parametrelendirilebilir. Her durumda gama dağılımını tanımlayan iki parametre pozitif gerçek sayılardır.

Tipik olarak gama dağılımı sağa çarpık veri kümelerini modellemek için kullanılır, böylece grafiğin sol tarafında daha fazla veri konsantrasyonu olur. Örneğin, gama dağılımı elektrikli bileşenlerin güvenilirliğini modellemek için kullanılır.

Gama dağılım diyagramı

Gama dağılımının grafiği, karakteristik parametrelerinin değerlerine bağlıdır. Aşağıda gama dağılımının yoğunluk fonksiyonunun şekil parametresine ve ölçek parametresine bağlı olarak nasıl değiştiğini görebilirsiniz.

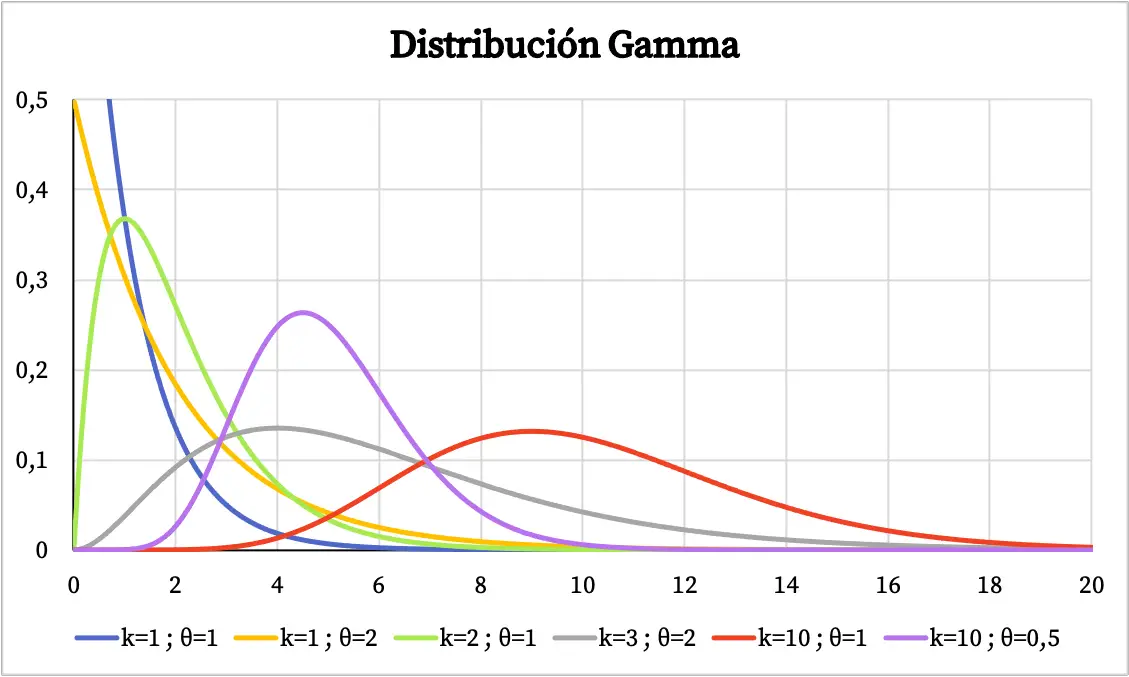
Öte yandan gama dağılımının kümülatif olasılık fonksiyonunun grafiğini aşağıda görebilirsiniz:

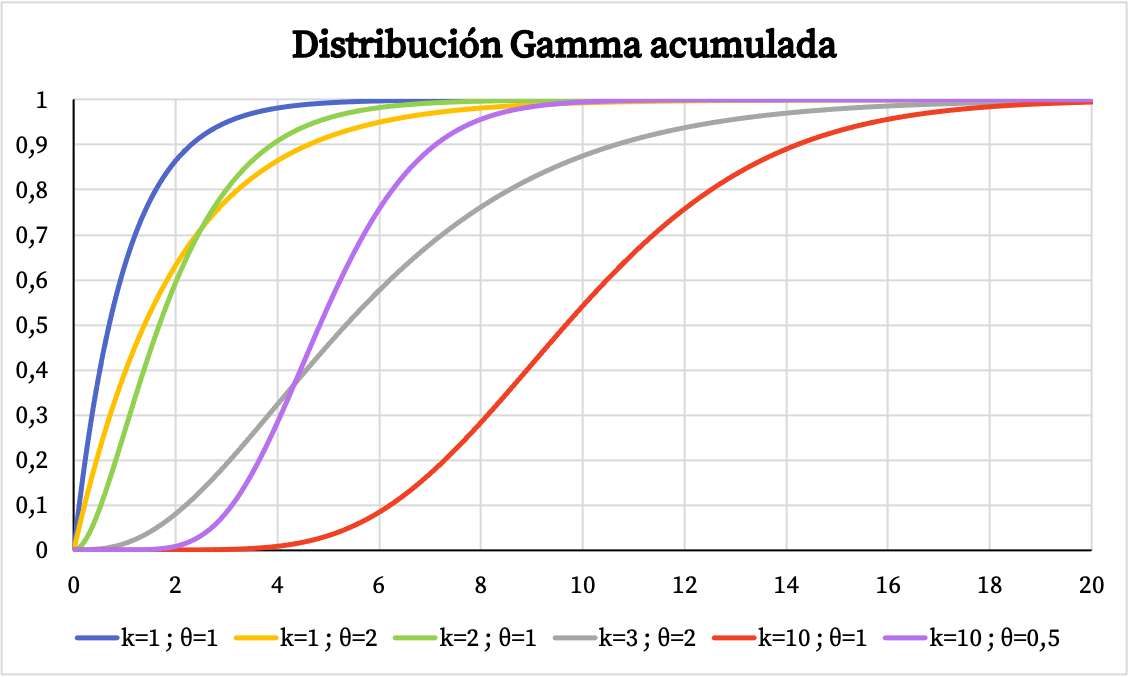
Gamm dağılımının kümülatif olasılık fonksiyonunun grafiği

Gama dağılımının özellikleri

Daha sonra gama dağılımının özelliklerinin neler olduğunu göreceğiz.

Gama dağılımının grafiği tamamen iki karakteristik parametresi ile tanımlanır: α şekil parametresidir ve λ ölçek parametresidir.

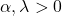
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li> Gama dağılımının alanı yalnızca pozitif sayılardan oluşur.</li> </ul> <p class=$ $x\in (0,+\infty)$

Gama dağılımının ortalaması, şekil parametresi ile ölçek parametresi arasındaki orana, yani α/λ’ya eşittir.

$E[X]=\cfrac{\alpha}{\lambda}$

Gama dağılımının varyansı, şekil parametresinin ölçek parametresinin karesine bölünmesine eşdeğerdir.

$Var(X)=\cfrac{\alpha}{\lambda^2}$

α’nın 1’den küçük değerleri için mod 0’dır. Ancak α 1’e eşit veya 1’den büyükse gama dağılımının modu aşağıdaki formülle hesaplanabilir:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

Gama dağılımının yoğunluk fonksiyonu formülü şöyledir:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Burada Γ şu şekilde tanımlanan gama fonksiyonudur:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

Gama dağılımıyla tanımlanan bir rastgele değişkenin kümülatif dağılımının formülü aşağıdaki gibidir:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

Şekil parametresi α 1’e eşitse, gama dağılımı aynı ölçek parametresi λ ile üstel bir dağılıma eşdeğerdir.

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

Ölçek parametresi λ bir ortalama olduğunda, gama dağılımı ki-kare dağılımının özel bir durumudur.

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Gama dağılımı nedir?

Gama dağılım diyagramı

Gama dağılımının özellikleri

yazar hakkında

Dr.benjamin anderson

Yorum ekle