Kümeler üzerinde işlemler: birleşim, kesişim, tümleyen ve fark

Bir küme, öğelerin bir koleksiyonudur.

Bir kümeyi büyük harfle belirtiriz ve kümenin elemanlarını küme parantezleri kullanarak tanımlarız. Örneğin, elemanları 1, 2, 3 olan “A” adında bir kümemiz olduğunu varsayalım. Bunu şu şekilde yazabiliriz:

bir = {1, 2, 3}

Bu eğitimde olasılık ve istatistikte en sık kullanılan küme işlemleri açıklanmaktadır.

birlik

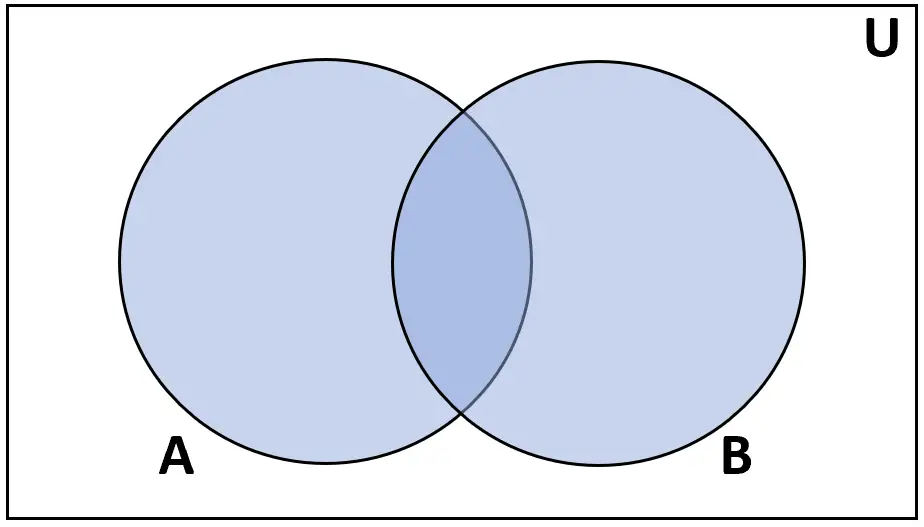
Tanım: A ve B kümelerinin birleşimi, A veya B’de bulunan elemanların kümesidir.

Derecelendirme: A ∪ B

Örnekler:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Kavşak

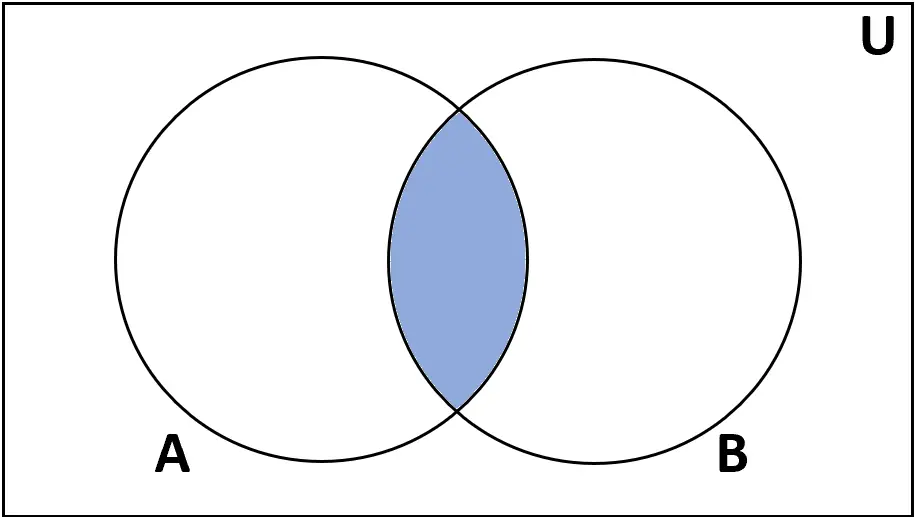
Tanım: A ve B kümelerinin kesişimi , hem A hem de B’de bulunan elemanların kümesidir.

Gösterim: A ∩ B

Örnekler:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Tamamlayıcı

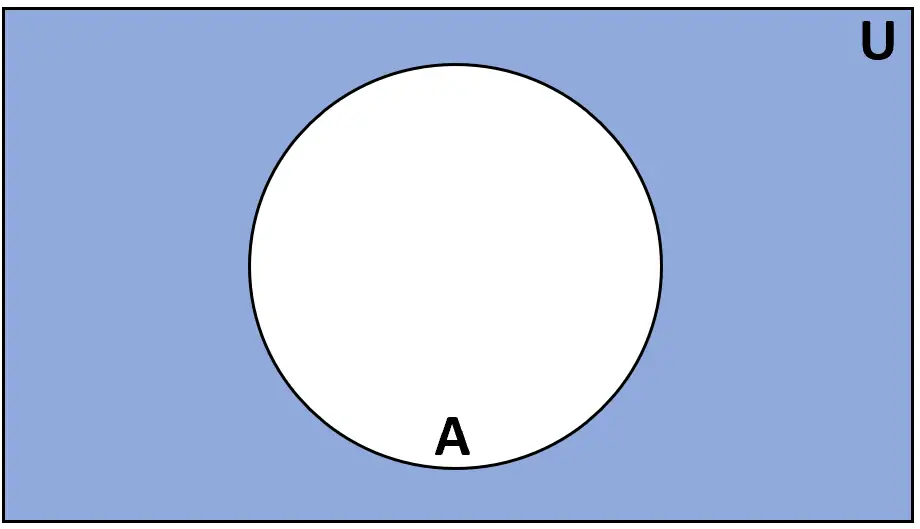
Tanım: A kümesinin tümleyeni , U evrensel kümesinde bulunan ancak A kümesinde olmayan elemanların kümesidir.

Derecelendirme: A’ veya ^Ac

Örnekler:

• Eğer U = {1, 2, 3, 4, 5, 6} ve A = {1, 2} ise A ^c = {3, 4, 5, 6}
• Eğer U = {1, 2, 3} ve A = {1, 2} ise A ^c = {3}

Fark

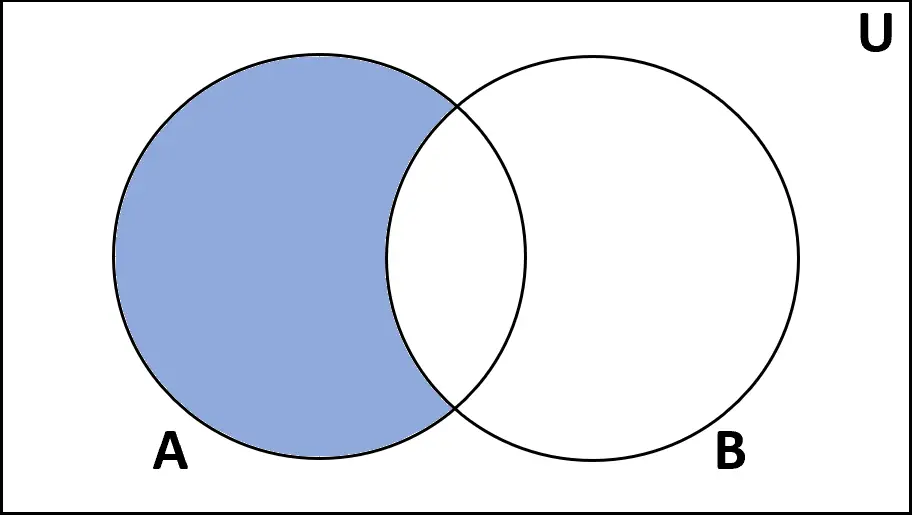
Tanım: A ve B kümeleri arasındaki fark , A’da bulunan ancak B’de bulunmayan elemanların kümesidir.

Derecelendirmeler: A–B

Örnekler:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Simetrik fark

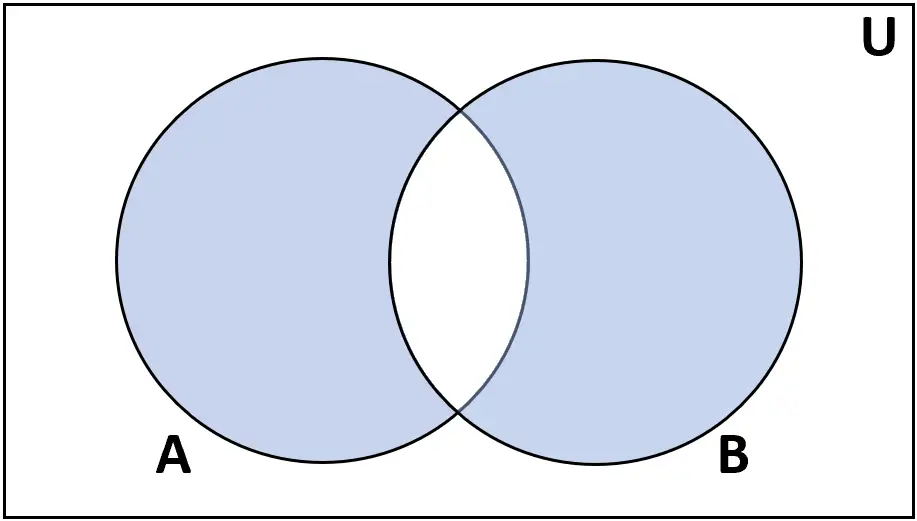
Tanım: A ve B kümelerinin simetrik farkı, A veya B’de bulunan, ancak her ikisinde de bulunmayan elemanların kümesidir.

Derecelendirme: AΔB

Örnekler:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

Kartezyen ürün

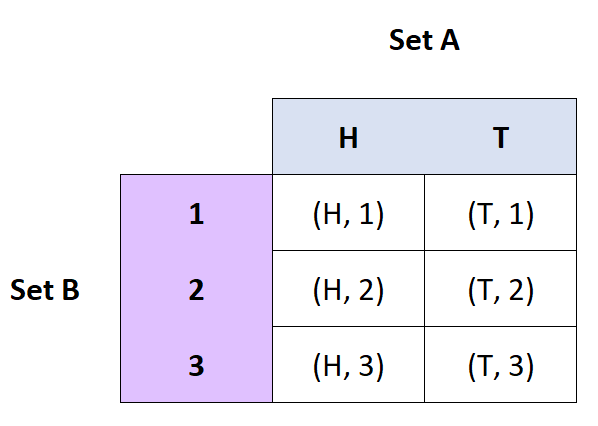
Tanım: A ve B kümelerinin Kartezyen çarpımı , A ve B’nin sıralı çiftlerinin kümesidir.

Derecelendirme: A x B

Örnekler:

• Eğer A = {H, T} ve B = {1, 2, 3} ise, bu durumda A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Eğer A = {T, H} ve B = {1, 2, 3} ise, bu durumda A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}