Geometrik dağılıma giriş

Geometrik dağılım, bir dizi Bernoulli denemesinde ilk başarıyı elde etmeden önce belirli sayıda başarısızlığın yaşanma olasılığını tanımlar.

Bir Bernoulli denemesi yalnızca iki olası sonucu olan bir deneydir – “başarılı” veya “başarısız” ve başarı olasılığı deney her yapıldığında aynıdır.

Bernoulli makalesinin bir örneği yazı tura atmaktır. Para yalnızca iki tura gelebilir (turalara “vuruş”, yazılara ise “başarısızlık” diyebiliriz) ve paranın adil olduğunu varsayarsak, her atışta başarı olasılığı 0,5’tir.

Eğer bir X rastgele değişkeni geometrik bir dağılım izliyorsa, ilk başarıyı elde etmeden önce k tane başarısızlığın yaşanma olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = (1-p) ^kp

Altın:

• k: ilk başarıdan önceki başarısızlık sayısı
• p: her denemede başarı olasılığı

Örneğin, adil bir yazı tura gelene kadar kaç kez atmamız gerektiğini bilmek istediğimizi varsayalım. 0, 1, 2, 3 arıza vb. yaşanma olasılığını belirlemek için yukarıdaki formülü kullanabiliriz. para tura gelmeden önce:

Not: Madeni para ilk atışta tura gelirse 0 “başarısızlık” yaşayabilir.

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Herhangi bir sayıda yazı tura atma olasılığını sonsuza kadar hesaplayabiliriz. Daha sonra bu olasılık dağılımını görselleştirmek için basit bir histogram oluşturuyoruz:

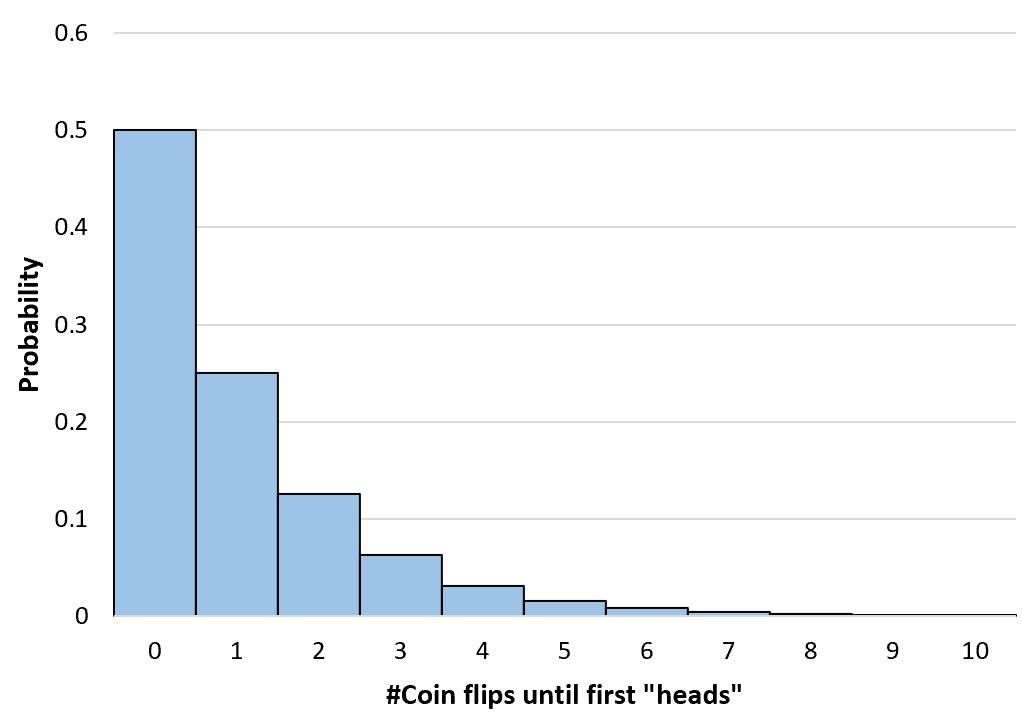
Kümülatif geometrik olasılıkların hesaplanması

İlk başarıya ulaşana kadar k veya daha az başarısızlık yaşamamızın kümülatif olasılığı aşağıdaki formülle bulunabilir :

P(X≤k) = 1 – (1-p) ^k+1

Altın:

• k: ilk başarıdan önceki başarısızlık sayısı
• p: her denemede başarı olasılığı

Örneğin, madeni paranın nihayet tura gelmesinden önce üç veya daha az “ıskalama”nın gerekli olma olasılığını bilmek istediğimizi varsayalım. Bu olasılığı hesaplamak için aşağıdaki formülü kullanırız:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Her kümülatif olasılığı benzer bir formül kullanarak hesaplayabiliriz:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Bu kümülatif olasılıkları, herhangi bir sayıdaki yazı-tura atışları için sonsuza kadar hesaplayabiliriz. Daha sonra bu kümülatif olasılık dağılımını görselleştirmek için bir histogram oluşturabiliriz:

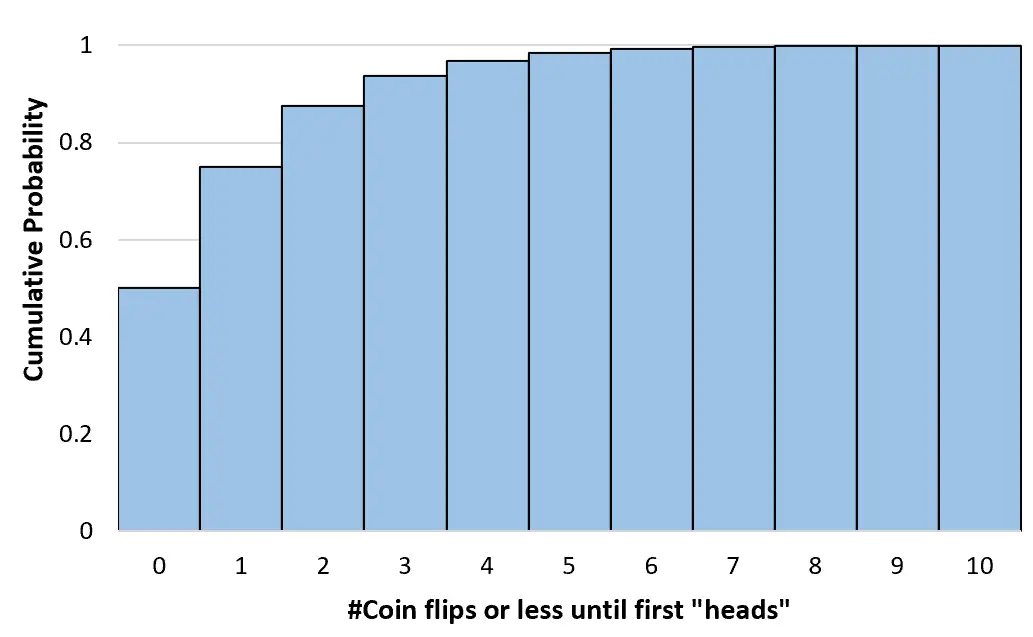
Geometrik dağılımın özellikleri

Geometrik dağılım aşağıdaki özelliklere sahiptir:

Dağılımın ortalaması (1-p) / p’dir .

Dağılımın varyansı (1-p) / p ^2’dir .

Örneğin:

Bir madalyonun yazı gelmeden önce tura gelmesini beklediğimiz ortalama sayı (1-p) / p = (1-.5) / .5 = 1 olacaktır.

Tura gelene kadar atış sayısının varyansı (1-p)/ ^p2 =(1-.5)/ olacaktır. ⁵² = 2 .

Geometrik Dağılım Uygulama Problemleri

Geometrik dağılım bilginizi test etmek için aşağıdaki alıştırma problemlerini kullanın.

Not: Bu soruların cevaplarını hesaplamak içinGeometrik Dağılım Hesaplayıcıyı kullanacağız.

Sorun 1

Soru: Bir araştırmacı, insanlara belirli bir yasayı destekleyip desteklemediklerini sormak için kütüphanenin önünde bekliyor. Belirli bir kişinin yasayı destekleme olasılığı p = 0,2’dir. Araştırmacının konuştuğu dördüncü kişinin yasayı ilk destekleyen kişi olma olasılığı nedir?

Cevap: İlk başarıya kadar “başarısızlık” sayısı, yani ilk kişi destekleyene kadar kanunu desteklemeyenlerin sayısı 3’tür. Yani p = 0,2 ve x olan geometrik dağılım hesaplayıcısı kullanıldığında = 3 başarısızlık, P(X=3) = 0,10240 olduğunu buluruz.

Sorun 2

Soru: Bir araştırmacı, insanlara belirli bir yasayı destekleyip desteklemediklerini sormak için kütüphanenin önünde bekliyor. Belirli bir kişinin yasayı destekleme olasılığı p = 0,2’dir. Araştırmacının yasayı destekleyen birini bulmak için dörtten fazla kişiyle konuşmak zorunda kalması olasılığı nedir?

Cevap: P =0,2 ve x = 4 hatalı geometrik dağılım hesaplayıcısını kullanarak P(X>4) = 0,32768’i buluruz.

Sorun 3

Soru: Bir araştırmacı, insanlara belirli bir yasayı destekleyip desteklemediklerini sormak için kütüphanenin önünde bekliyor. Belirli bir kişinin yasayı destekleme olasılığı p = 0,2’dir. Araştırmacının yasayı destekleyen birini bulana kadar konuşması gereken tahmini kişi sayısı nedir?

Cevap: Geometrik dağılımın ortalamasının (1-p) / p olduğunu hatırlayın. Bu durumda ortalama (1-.2) / .2 = 4 olacaktır.