Excel'de geometrik dağılım nasıl kullanılır?

Geometrik dağılım, bir dizi Bernoulli denemesinde ilk başarıyı elde etmeden önce belirli sayıda başarısızlığın yaşanma olasılığını tanımlar.

Bir Bernoulli denemesi yalnızca iki olası sonucu olan bir deneydir – “başarılı” veya “başarısız” ve başarı olasılığı deney her yapıldığında aynıdır.

Bernoulli makalesinin bir örneği yazı tura atmaktır. Para yalnızca iki tura gelebilir (turalara “vuruş”, yazılara ise “başarısızlık” diyebiliriz) ve paranın adil olduğunu varsayarsak, her atışta başarı olasılığı 0,5’tir.

Eğer bir X rastgele değişkeni geometrik bir dağılım izliyorsa, ilk başarıyı elde etmeden önce k tane başarısızlığın yaşanma olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = (1-p) ^kp

Altın:

• k: ilk başarıdan önceki başarısızlık sayısı
• p: her denemede başarı olasılığı

Aşağıdaki örnekler Excel’de geometrik dağılımla ilgili olasılıkların nasıl hesaplanacağını gösterir.

Örnek 1: Yazı tura atma

Diyelim ki bir yazı tura atıyoruz ve yazı tura gelene kadar tam olarak üç “ıskalama”nın geçmesi olasılığını bilmek istiyoruz.

Bu olasılığı hesaplamak için aşağıdaki formülü kullanırız:

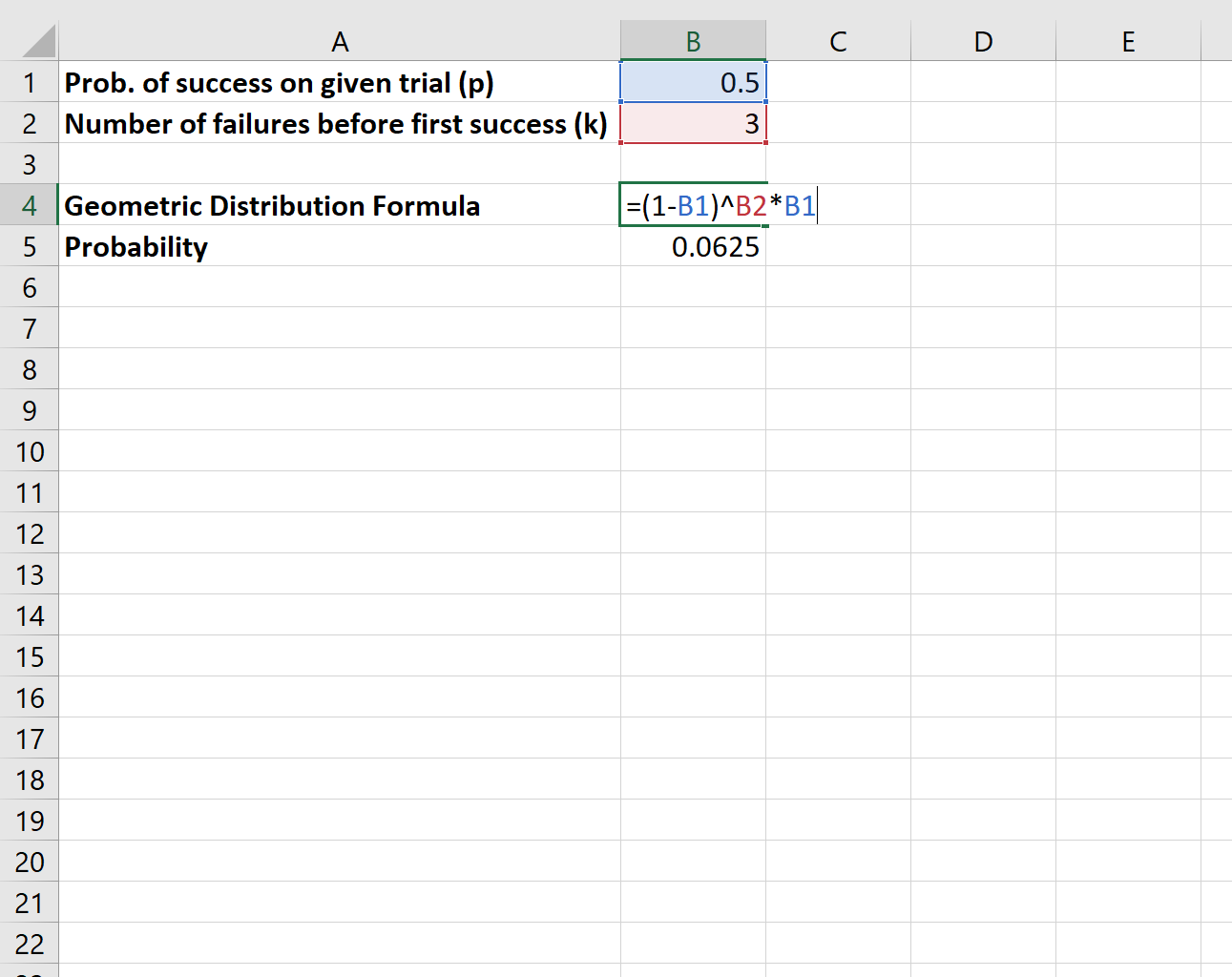
Bir madeni para sonunda tura gelene kadar üç “ıskalama” yaşama olasılığımız 0,0625’tir .

Örnek 2: Serbest atış atışı

Diyelim ki bir basketbol oyuncusu serbest atışlarının %60’ını yapıyor. Oyuncunun sonunda bir atış yapana kadar dört serbest atış kaçırma olasılığı nedir?

Bu olasılığı hesaplamak için aşağıdaki formülü kullanırız:

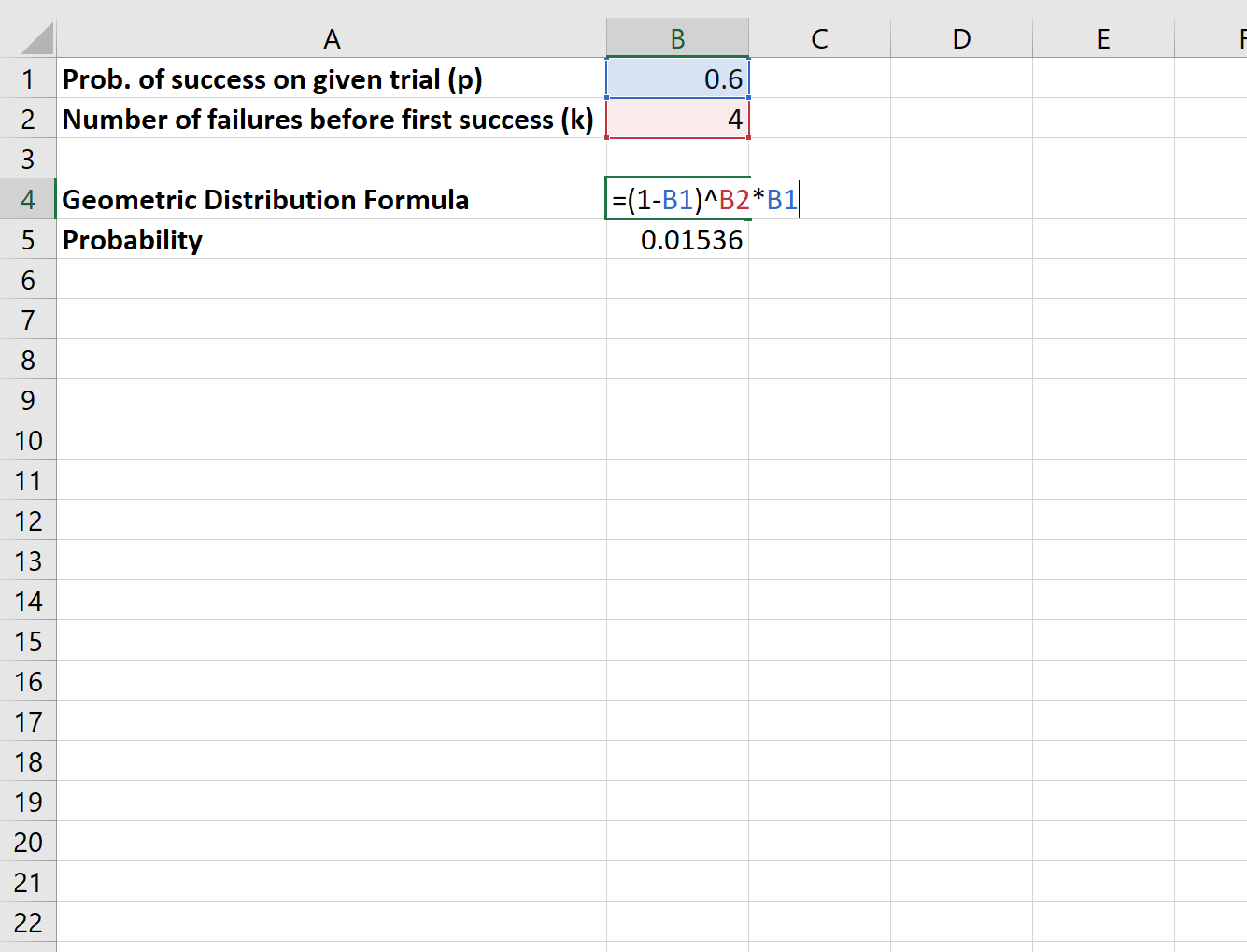
Oyuncunun sonunda bir atış yapana kadar dört serbest atış kaçırma olasılığı 0,01536’dır .

Örnek 3: Bir yasanın desteklenmesi

Bir araştırmacının kütüphanenin önünde beklediğini ve insanlara belirli bir yasayı destekleyip desteklemediklerini sorduğunu varsayalım. Belirli bir kişinin yasayı destekleme olasılığı p = 0,2’dir. Araştırmacının konuştuğu dördüncü kişinin yasayı ilk destekleyen kişi olma olasılığı nedir?

Bu olasılığı hesaplamak için aşağıdaki formülü kullanırız:

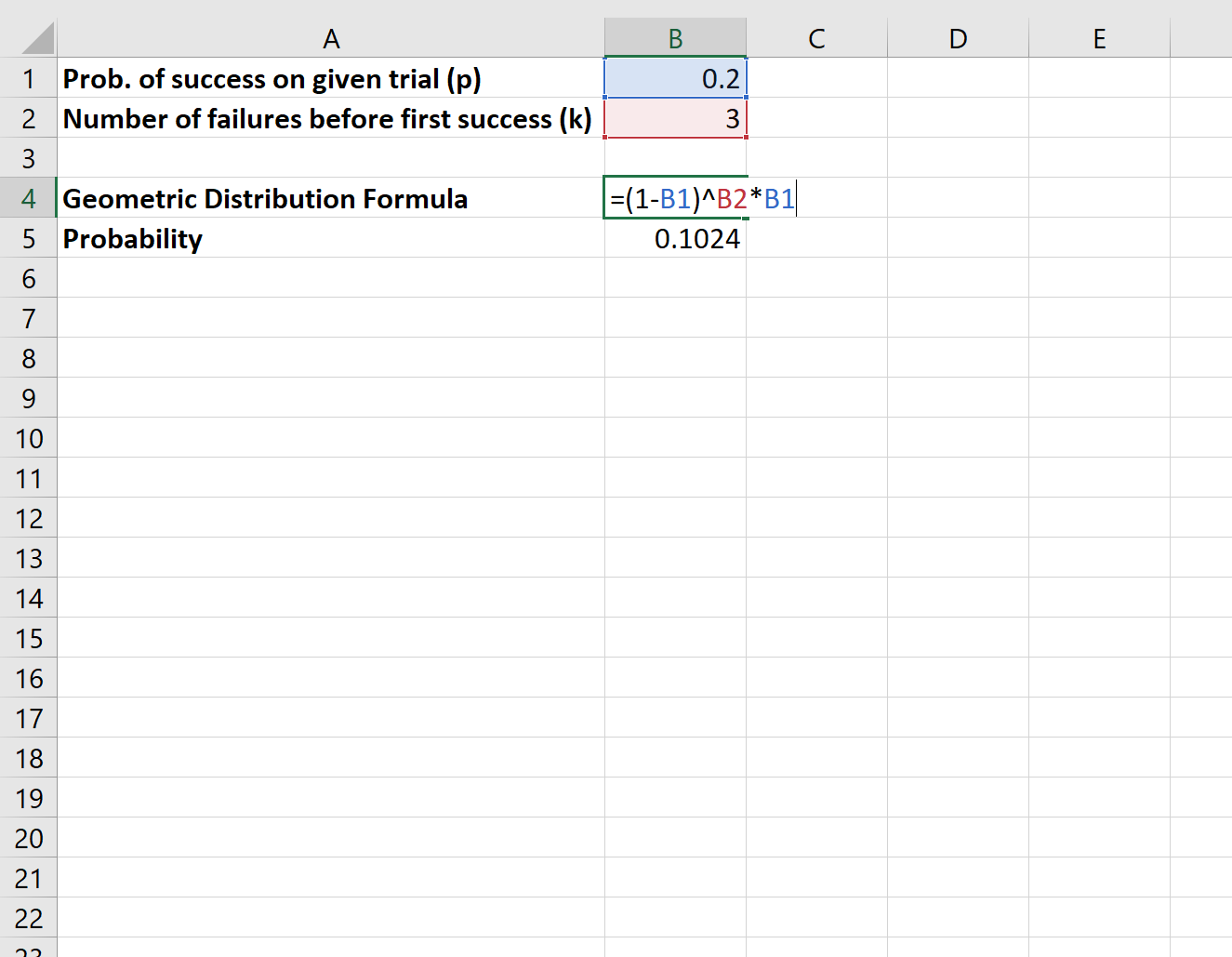
Araştırmacının konuştuğu dördüncü kişinin yasayı ilk destekleyen kişi olma olasılığı 0,1024’tür .

Ek kaynaklar

Geometrik dağılıma giriş
Geometrik Dağılım Hesaplayıcı
Geometrik dağılıma 5 somut örnek