Geometrik araçlar

İle Dr.benjamin anderson Ağustos 6, 2023 İstatistik 0 Yorum

Bu yazımızda geometrik ortalamanın ne olduğunu, nasıl hesaplandığını ve geometrik ortalama ile aritmetik ortalama arasındaki farkın ne olduğunu açıklayacağız. Ayrıca geometrik ortalamanın adım adım çözülmüş alıştırmasını ve bu tür ortalamanın özelliklerinin neler olduğunu görebileceksiniz. Son olarak herhangi bir veri kümesinin geometrik ortalamasını hesaplayacak bir hesap makinesi bulacaksınız.

Geometrik ortalama nedir?

Geometrik ortalama, tanımlayıcı istatistiklerin merkeziliğinin bir ölçüsüdür. Bir istatistiksel veri kümesinin geometrik ortalaması, tüm değerlerin çarpımının n’inci köküne eşittir.

Geometrik ortalama, işletme finansmanında getiri oranlarını, ortalama yüzdeleri ve bileşik faizi hesaplamak için kullanılır.

Bu nedenle geometrik ortalamanın formülü aşağıdaki gibidir:

Geometrik ortalama yalnızca örnekteki tüm veriler pozitif olduğunda hesaplanabilir. Çünkü bir değer negatifse kökün negatif çözümü olur veya çözümü olmaz, öte yandan veri sıfırsa verinin çarpımı sıfır verir ve dolayısıyla geometrik ortalama 0 olur.

Geometrik ortalama, var olan tek ortalama türü değildir; aritmetik ortalama, ağırlıklı ortalama, kare ortalama ve harmonik ortalama da vardır.

Geometrik ortalama ile aritmetik ortalama arasındaki fark

Geometrik ortalama ile aritmetik ortalama arasındaki temel fark , geometrik ortalamanın uç değerlere aritmetik ortalamaya göre daha az duyarlı olmasıdır. Ayrıca aritmetik ortalama negatif ve sıfır değerlerle, geometrik ortalama ise yalnızca pozitif değerlerle hesaplanabilmektedir.

Benzer şekilde, aynı veri seti için geometrik ortalama genellikle aritmetik ortalamadan daha düşük olacaktır.

Geometrik ortalamanın hesaplanmasının daha karmaşık olduğu ve bu nedenle istatistiksel anlamlılığının yorumlanmasının daha zor olduğu da unutulmamalıdır.

Kısaca geometrik ortalamanın aritmetik ortalamaya göre avantaj ve dezavantajları vardır ve verinin niteliğine göre şu veya bu ortalamanın hesaplanması uygun olacaktır.

Geometrik ortalama nasıl hesaplanır

Geometrik ortalamayı hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

Örnekteki tüm istatistiksel verilerin çarpımını hesaplayın.
Hesaplanan çarpımın n’inci kökünü bulun.
Elde edilen sonuç istatistiksel örneğin geometrik ortalamasıdır.

Gördüğünüz gibi, bir veri kümesinin geometrik ortalamasını bulmak, bir hesap makinesi veya bilgisayar programıyla nispeten basittir, çünkü yalnızca bir çarpımı ve bir kökü hesaplamanız gerekir. Tam tersine hesaplamayı elle yapmak oldukça zahmetlidir.

👉Bu nedenle bir veri kümesinin geometrik ortalamasını hesaplamak için aşağıdaki hesap makinesini kullanmanızı öneririz.

Geometrik Ortalama Örneği

Geometrik ortalamayla ilgili teoriyi gördükten sonra, geometrik ortalamanın tam olarak nasıl elde edileceğini görebilmeniz için bir örnek yapacağız.

Bir şirketin son beş yıllık ekonomik sonuçları bilinmektedir. İlk yıl ekonomik karlılık %10, ikinci yıl kar %23, üçüncü yıl kazanılan para %16, dördüncü yıl ise %7 ekonomik karlılık elde edildi ve yatırım beşinci yılda %20’lik bir getiriyi temsil ediyordu. Tüm yüzdelerin ortalamasını hesaplamanız istenir.

Gördüğümüz gibi yüzdelerin ortalamasını hesaplamak için aritmetik ortalamayı kullanmamalı, hesaplamayı geometrik ortalamayla yapmalısınız.

Bu nedenle geometrik ortalama formülünü uyguluyoruz:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

Örnek değerleri formülde yerine koyup hesaplamayı gerçekleştiriyoruz:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Beş veri noktamız olduğunu unutmayın, dolayısıyla beşinci kökü hesaplıyoruz.

Geometrik ortalamanın sayısal sonucu 1,15 olup, bu da şirketin her yıl ortalama %15 oranında ekonomik büyüme yaşadığı anlamına gelmektedir.

Tüm değerlerin pozitif olması nedeniyle geometrik ortalamayı elde edebildiğimizi, ancak herhangi bir yüzde negatif olsaydı formüldeki verileri tamsayı kısmıyla birlikte pozitif bir ondalık sayı olarak koymak zorunda kalacağımızı unutmayın. sıfıra eşittir. Örneğin -%30’luk büyüme formülde 0,70 (1-0,3=0,7) olarak ifade edilmelidir.

Geometrik Ortalama Hesaplayıcı

Geometrik ortalamasını bulmak için herhangi bir örnek istatistiği aşağıdaki hesap makinesine takın. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir. Bir değerin negatif veya sıfır olması durumunda geometrik ortalamayı belirleyemeyeceğinizi unutmayın.

Geometrik ortalamanın özellikleri

Geometrik ortalama aşağıdaki özelliklere sahiptir:

Bu, yüzdelerin veya endekslerin ortalamasını bulmak için çok yararlı olan bir ortalama türüdür.

Yalnızca tüm verilerin pozitif olması durumunda hesaplanabilir.

A ve b sayılarının geometrik ortalamasının geometrik anlamı, kenarları a ve b olan dikdörtgenle aynı alana sahip bir karenin bir kenarıdır.

$MG(a,b)=\sqrt{a\cdot b}$

Üç a , b ve c sayısının geometrik ortalamasının geometrik anlamı, hacmi a , b ve c kenarlarının paralelkenarına eşit olan bir küpün tarafıdır.

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Bir veri kümesinin geometrik ortalamasının logaritması, aynı kümenin logaritmasının aritmetik ortalamasını verir.

Bir değerler kümesinin geometrik ortalaması her zaman aritmetik ortalamadan küçük veya ona eşit olacaktır.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Ağırlıklı geometrik ortalama, geometrik ortalamayla aynı şekilde hesaplanır, ancak istatistiksel değerleri ağırlıklandırmak için her veri öğesinin üssüne ağırlıklar eklenerek hesaplanır.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

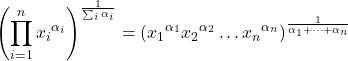
Excel’de geometrik ortalamayı hesaplayın

Son olarak Excel programını kullanarak bir veri setinin geometrik ortalamasını nasıl bulacağımızı görelim.

Excel’de geometrik ortalamayı hesaplamak için MEANS.GEOM işlevini kullanmanız gerekir. Geometrik ortalamasını almak istediğiniz tüm değerleri girmeniz yeterlidir; fonksiyon geometrik ortalama sonucunu döndürecektir.

Örneğin, yukarıda çalışılan örneğin geometrik ortalamasını belirlemek için bir Excel kutusuna =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) yazmanız gerekir.

Değerlerden herhangi birinin sıfır veya negatif olması durumunda fonksiyonun hata döndüreceğini unutmamalısınız.

Gördüğünüz gibi, verileri bir sayfaya kopyalayıp bir formül kullanmanız yeterli olduğundan, Excel’de geometrik ortalamayı hesaplamak çok daha basit ve hızlıdır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil