Besin testi nedir? (açıklama & örnek)
Chow testi, ekonomist Gregory Chow tarafından geliştirilen ve iki farklı regresyon modelinin farklı veri setleri üzerindeki katsayılarının eşit olup olmadığını test etmek için kullanılan istatistiksel bir testtir.
Chow testi tipik olarak ekonometri alanında zaman serisi verileriyle belirli bir zamanda verilerde yapısal bir kırılma olup olmadığını belirlemek için kullanılır.
Örneğin aşağıdaki dağılım grafiğini göz önünde bulundurun:
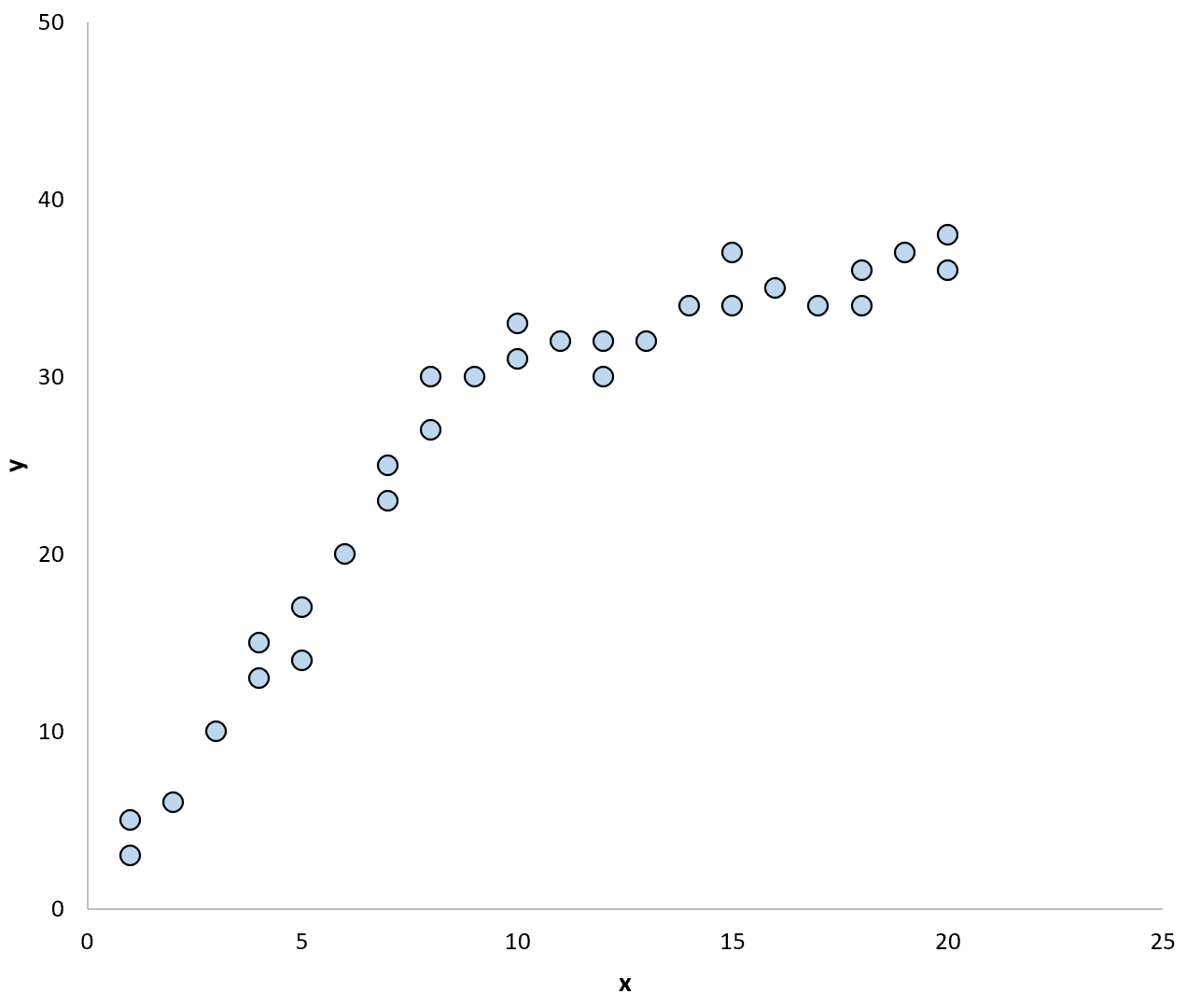
Verilerdeki modeli özetlemek için bir regresyon çizgisi kullansaydık şöyle görünebilir:
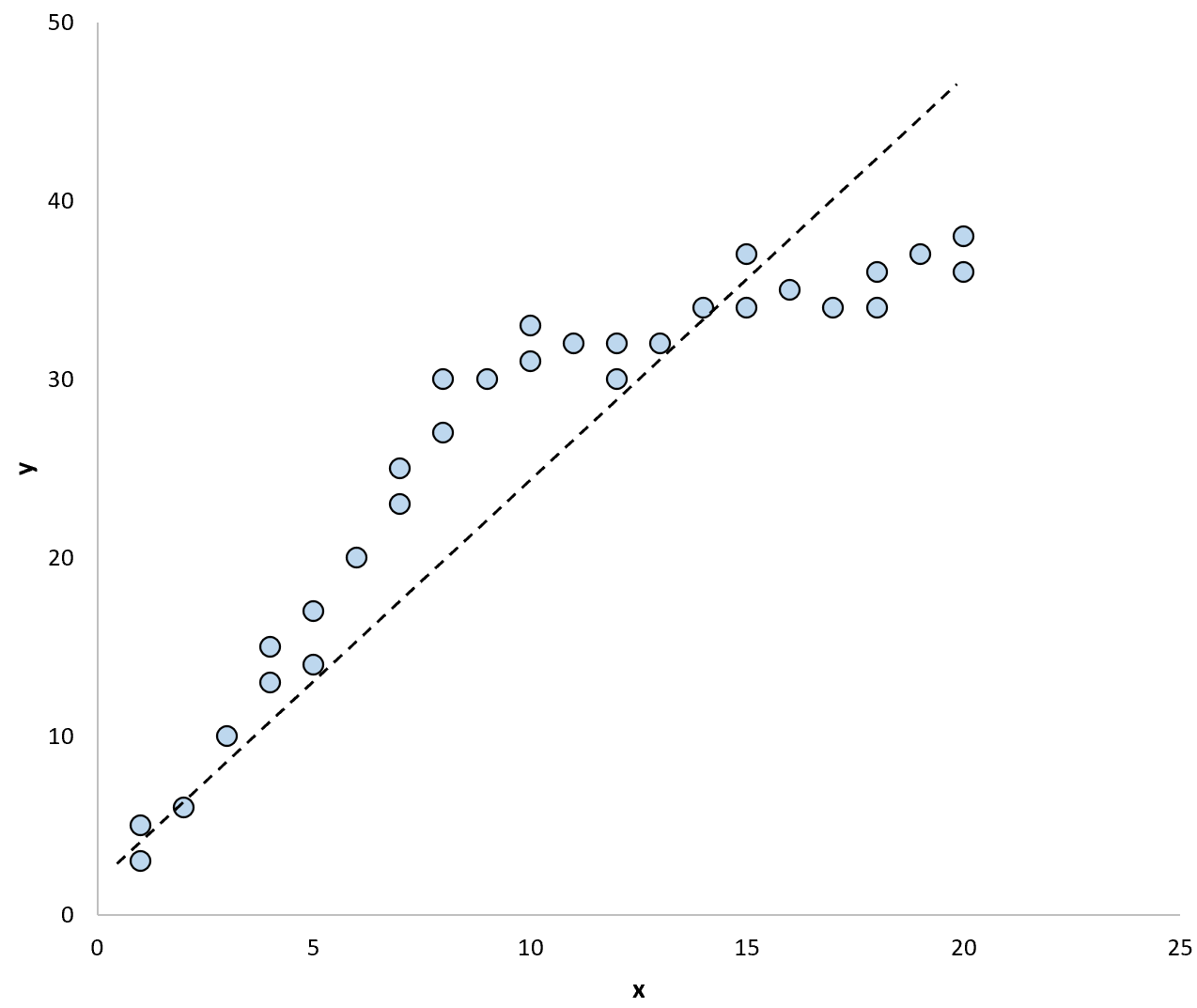
Verilerdeki modeli özetlemek için iki ayrı regresyon çizgisi kullanırsak şöyle görünebilir:
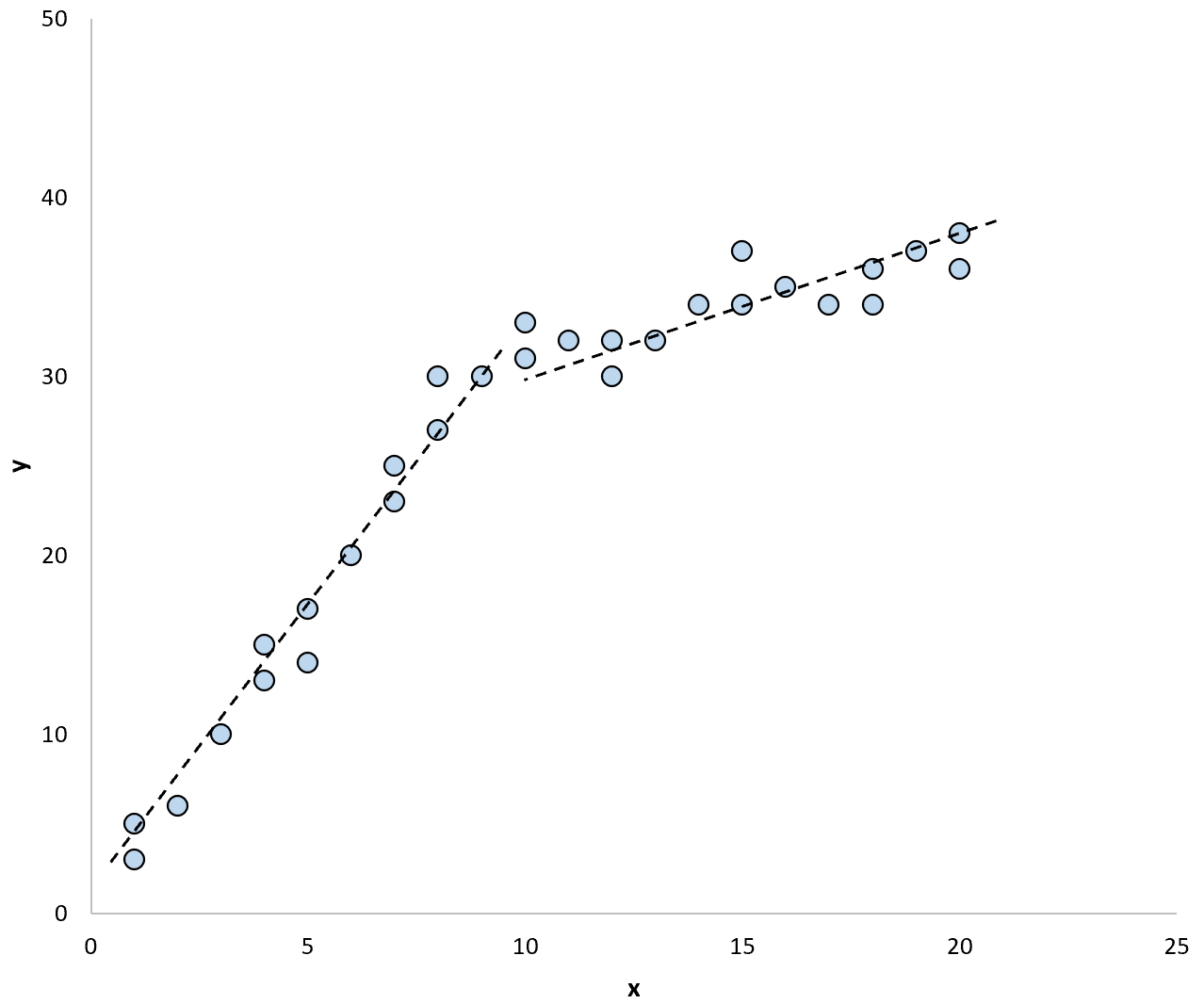
Chow testi, her bir regresyon çizgisinin regresyon katsayılarının eşit olup olmadığını test etmemizi sağlar.
Test, katsayıların regresyon çizgileri arasında eşit olmadığını belirlerse, bu, verilerde yapısal bir kırılmaya dair önemli bir kanıt olduğu anlamına gelir. Yani bu yapısal kırılma noktası öncesi ve sonrası veri trendi çok farklı.
Chow testi ne zaman kullanılmalı?
Aşağıdaki örnekler Chow testi yapmak isteyebileceğiniz durumları göstermektedir:
1. Hisse senedi fiyatlarının seçim öncesinde ve sonrasında farklı oranlarda hareket edip etmediğini belirleyin.
2. Faiz oranı değişiminden önce ve sonra konut fiyatlarının değişip değişmediğini belirleyin.
3. Yeni vergi kanununun kabul edilmesinden önce ve sonra kamu işletmelerinin ortalama kârının farklı olup olmadığının belirlenmesi.
Her durumda, herhangi bir zamanda verilerde yapısal bir kırılma noktası olup olmadığını belirlemek için bir Chow testi kullanabiliriz.
Chow Testi Gerçekleştirme Adımları
Chow testi gerçekleştirmek için aşağıdaki adımları kullanabiliriz.
Adım 1: Sıfır ve alternatif hipotezleri tanımlayın.
Aşağıdaki regresyon modelini veri setimizin tamamına uyarladığımızı varsayalım:
- y t = a + bx 1t + cx t2 + ε
Daha sonra, verilerimizi yapısal bir kırılma noktasına göre iki gruba ayırdığımızı ve her gruba aşağıdaki regresyon modellerini yerleştirdiğimizi varsayalım:
- y t = a 1 + b 1 x 1t + c 1 x t2 + ε
- y t = a 2 + b 2 x 1t + c 2 x t2 + ε
Chow testi için aşağıdaki boş ve alternatif hipotezleri kullanırız:
- Boş (H 0 ): a 1 = a 2 , b 1 = b 2 ve c 1 = c 2
- Alternatif ( HA ): Null’daki karşılaştırmalardan en az biri eşit değil.
Sıfır hipotezini reddedersek, verilerde yapısal bir kırılma noktası olduğunu ve iki regresyon çizgisinin verilere birden daha iyi uyum sağlayabileceğini söyleyecek yeterli kanıtımız olur.
Sıfır hipotezini reddetmeyi başaramazsak, verilerde yapısal bir kırılma noktası olduğunu söyleyecek yeterli kanıtımız yoktur. Bu durumda, regresyon çizgilerinin, veri modelini yeterince iyi temsil eden tek bir regresyon çizgisi halinde “toplanabileceğini” söylüyoruz.
Adım 2: Test istatistiğini hesaplayın.
Aşağıdaki terimleri tanımlarsak:
- S T : Toplam verinin artıklarının karelerinin toplamı
- S 1 , S 2 : her grubun artıklarının karelerinin toplamı
- N 1 , N 2 : Her gruptaki gözlem sayısı
- k: Parametre sayısı
O zaman Chow test istatistiğinin şu şekilde olduğunu söyleyebiliriz:
Chow testi istatistiği = [(S T – (S 1 +S 2 ))/k] / [(S 1 +S 2 )/ (N 1 +N 2 -2k)]
Bu test istatistiği, k ve N 1 +N 2 -2k serbestlik dereceleriyle F dağılımını takip eder.
Adım 3: Sıfır hipotezini reddedin veya reddetmeyin.
Bu test istatistiğine ilişkin p değeri belirli bir anlamlılık düzeyinin altındaysa sıfır hipotezini reddedebilir ve verilerde yapısal bir kırılma noktası olduğu sonucuna varabiliriz.
Neyse ki, çoğu istatistiksel yazılım Chow testini gerçekleştirme kapasitesine sahiptir, bu nedenle muhtemelen testi hiçbir zaman manuel olarak yapmak zorunda kalmayacaksınız.
Chow testi gerçekleştirme örneği
R’de belirli bir veri kümesi için Chow testinin nasıl gerçekleştirileceğine ilişkin adım adım bir örnek görmek için bu eğitime bakın.
Chow Test Notları
Chow testi hakkında akılda tutulması gereken bazı notlar:
1. Test, regresyon modellerinin artıklarının, varyansı bilinmeyen bir normal dağılımdan bağımsız ve aynı şekilde dağıtıldığını varsayar.
2. Chow testi yalnızca test etmek istediğiniz yapısal kırılmanın bilinen bir zamanda meydana gelmesi durumunda kullanılmalıdır. Başka bir deyişle test, belirli bir anın yapısal bir kırılma olarak kabul edilip edilemeyeceğini belirlemek için tekrar tekrar kullanılmamalıdır.
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil