Google e-tablolarda korelasyon matrisi nasıl oluşturulur

İki değişken arasındaki ilişkiyi ölçmenin bir yolu , iki değişken arasındaki doğrusal ilişkinin bir ölçüsü olan Pearson korelasyon katsayısını kullanmaktır . -1 ile 1 arasında bir değere sahiptir; burada:

• -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
• 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
• 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir

Korelasyon katsayısı sıfırdan ne kadar uzaksa, iki değişken arasındaki ilişki o kadar güçlüdür.

Ancak bazı durumlarda birden fazla değişken çifti arasındaki korelasyonu anlamak isteriz. Bu durumlarda, değişkenlerin çeşitli ikili kombinasyonları arasındaki korelasyon katsayılarını gösteren kare bir tablo olan bir korelasyon matrisi oluşturabiliriz.

Bu eğitimde Google E-Tablolar’da bir korelasyon matrisinin nasıl oluşturulacağı ve yorumlanacağı açıklanmaktadır.

Google E-Tablolarda Korelasyon Matrisi Nasıl Oluşturulur

Diyelim ki 10 basketbolcunun ortalama sayı, ribaund ve asist sayılarını gösteren aşağıdaki veri setine sahibiz:

Bu veri kümesi için bir korelasyon matrisi oluşturmak amacıyla CORREL() işlevini aşağıdaki sözdizimiyle kullanabiliriz:

  COVAR(veri_y; veri_x)

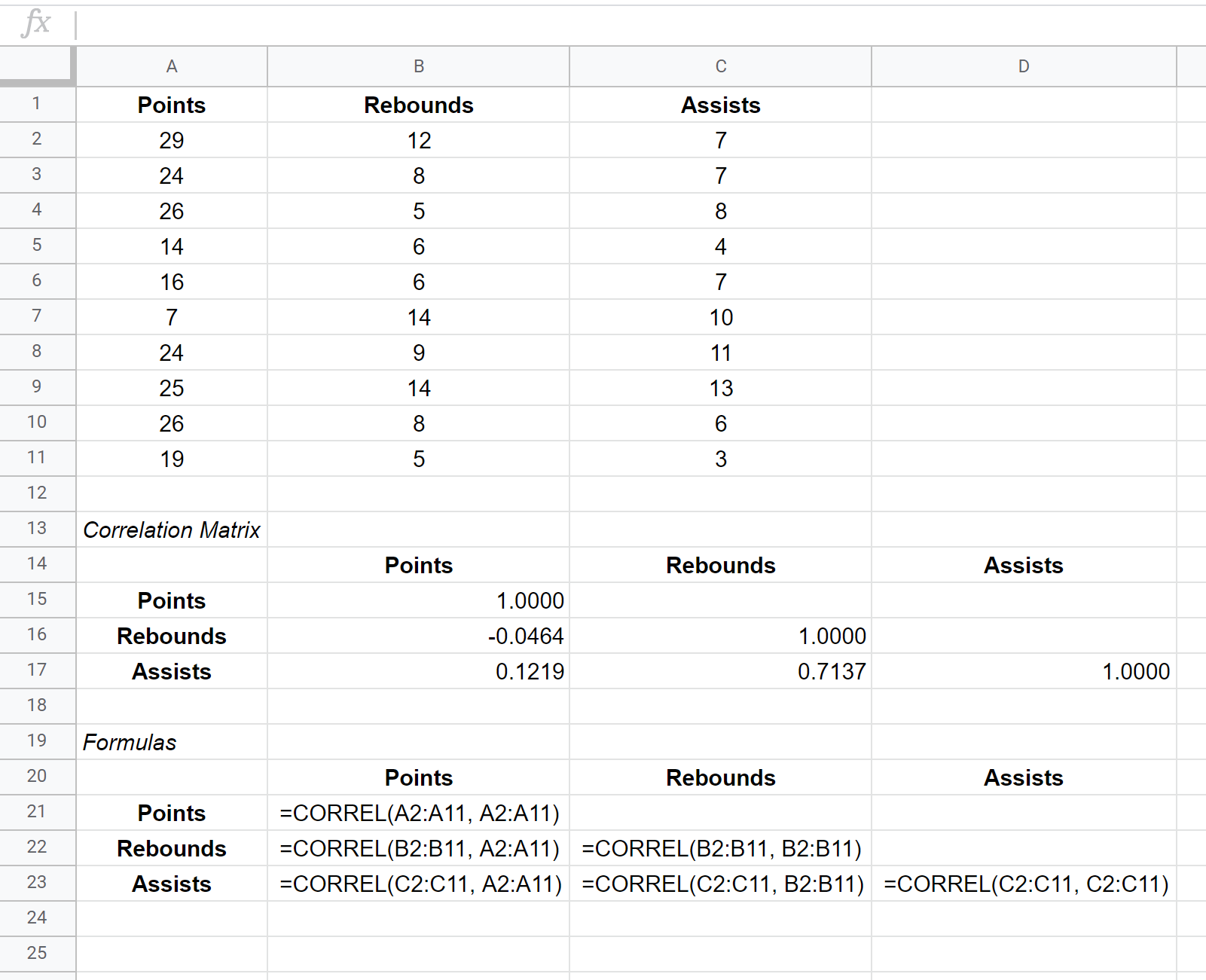
Bu veri kümesinin kovaryans matrisi B15:D17 hücrelerinde gösterilirken, kovaryans matrisini oluşturmak için kullanılan formüller aşağıdaki B21:D23 hücrelerinde gösterilmektedir:

Korelasyon matrisi nasıl yorumlanır?

Korelasyon matrisinin bireysel hücrelerindeki değerler bize değişkenlerin her ikili kombinasyonu arasındaki Pearson korelasyon katsayısını anlatır. Örneğin:

Sayılar ve ribauntlar arasındaki korelasyon: -0,0464. Sayılar ve ribaundlar arasında biraz negatif korelasyon var ancak bu değer sıfıra o kadar yakın ki bu iki değişken arasında anlamlı bir ilişki olduğuna dair güçlü bir kanıt yok.

Sayılar ve asistler arasındaki korelasyon: 0,1219. Sayılar ve asistler arasında hafif bir pozitif korelasyon var ancak bu değer de sıfıra oldukça yakın, dolayısıyla bu iki değişken arasında anlamlı bir ilişki olduğuna dair güçlü bir kanıt yok.

Ribaund ve asist arasındaki korelasyon: 0,7137. Ribaundlar ve asistler arasında güçlü bir pozitif korelasyon vardır. Yani daha fazla ribaund alan oyuncular aynı zamanda daha fazla asist yapma eğilimindedir.

Bir değişken ile kendisi arasındaki korelasyon her zaman 1 olduğundan korelasyon matrisinin köşegen değerlerinin hepsinin 1 olduğuna dikkat edin. Pratikte bu sayının yorumlanması yararlı değildir.

Ek kaynaklar

Korelasyon matrisi nasıl okunur
Excel’de Korelasyon Matrisi Nasıl Oluşturulur