Göreceli frekans

Bu makalede istatistikte bağıl frekansın ne olduğunu, bağıl frekansın nasıl elde edileceğini ve bağıl frekansla ilgili adım adım çözülmüş iki alıştırmayı öğreneceksiniz.

Göreceli frekans nedir?

İstatistiklerde göreceli frekans , bir değerin bir veri örneğinde oran veya yüzde olarak kaç kez göründüğünü gösteren bir ölçüdür. Daha doğrusu, bağıl frekans, mutlak frekansın toplam veri sayısına bölünmesine eşittir.

Örneğin bir değerin mutlak frekansı 15 ise ve toplamda 100 veri noktası varsa o değerin bağıl frekansı 0,15’tir (15/100=0,15).

Genellikle h _i sembolü bağıl frekansı temsil etmek için kullanılır. İstatistik camiasında hala bir fikir birliği olmamasına rağmen, başka bir sembolle temsil edilen göreceli sıklığı görebilirsiniz.

Göreceli frekans nasıl hesaplanır

Göreli frekans, mutlak frekansın toplam veri sayısına bölünmesine eşittir. Bu nedenle bağıl frekansı hesaplamak için önce mutlak frekansı bulmanız ve ardından bunu toplam gözlem sayısına bölmeniz gerekir.

Dolayısıyla bağıl frekans formülü aşağıdaki gibidir:

Altın:

• 

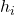
  bağıl frekanstır.

• 

  mutlak frekanstır.

• 

  toplam veri sayısıdır.

Öte yandan, göreceli frekansı yüzde cinsinden hesaplamak için, yani yüzde olarak ifade edilen göreceli frekansı hesaplamak için önceki formülü 100 ile çarpmanız yeterlidir:

Göreli Frekans Örnekleri

Göreceli frekansın tanımını gördükten sonra, aşağıda gerçek dünyadan iki örnek verilmiştir; böylece bu tür frekansın nasıl hesaplandığını görebilirsiniz. İlk örnekte ayrık bir değişkenin, ikinci örnekte ise sürekli bir değişkenin bağıl frekansı belirlenir.

Örnek 1: ayrık değişken

• 30 kişilik bir sınıfta istatistik konusunda alınan notlar aşağıdaki gibidir. Her notanın göreceli frekansı nedir?

Bu alıştırmadaki değişken ayrıktır çünkü veriler yalnızca tam sayılar olabilir; bu nedenle verileri aralıklar halinde gruplandırmaya gerek yoktur.

Bağıl frekansı bulmak için önce mutlak frekansı belirlememiz gerekir. Böylece bir frekans tablosu oluşturuyoruz ve her farklı değer için mutlak frekansı hesaplıyoruz:

Artık mutlak frekansı hesapladığımıza göre bağıl frekansı da hesaplayabiliriz. Bunu yapmak için, her mutlak frekansı toplam veri sayısına (30) bölmeniz yeterlidir:

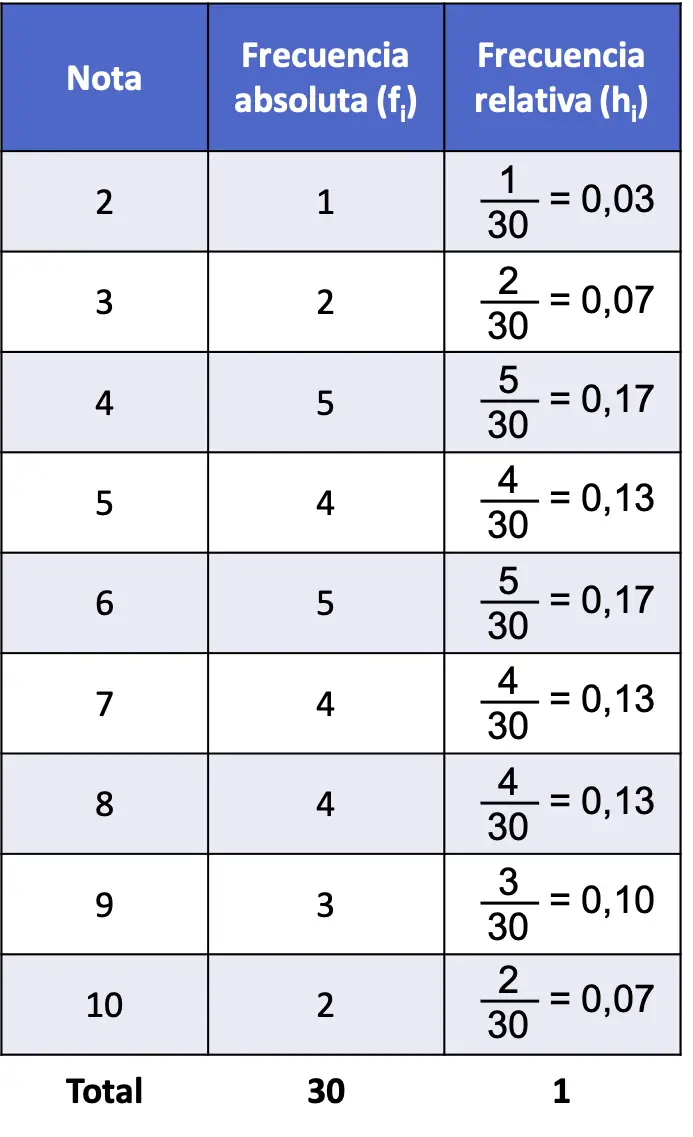
Yani problemin mutlak frekans ve bağıl frekans ile frekans tablosu aşağıdaki gibidir:

Tüm bağıl frekansların toplamının her zaman 1 verdiğini unutmayın; aksi halde bu, bazı hesaplamaların yanlış olduğu anlamına gelir.

Örnek 2: sürekli değişken

• 20 kişinin boyu ölçüldü ve aşağıda belirtilen sonuçlar elde edildi. Verileri aralıklara ayırın ve her aralığın göreceli sıklığını bulun.

Bu istatistiksel örnekteki veriler ondalık sayı olduğundan sürekli bir değişkene aittir ve bu nedenle değişken herhangi bir değeri alabilir. Bu nedenle, frekans hesaplamalarını yapmadan önce, verileri ilk olarak onda 10 genliğe sahip aralıklarla gruplandıracağız.

Daha sonra, her aralığın mutlak frekansını içeren bir frekans tablosu hazırlıyoruz:

Mutlak frekansı bulduktan sonra, her aralığın göreceli frekansını, mutlak frekansını toplam veri sayısına (20) bölerek elde edebiliriz:

Kümülatif bağıl frekans

Adından da anlaşılacağı üzere kümülatif bağıl frekans, istatistikte kullanılan ve bağıl frekanstan hesaplanan bir diğer frekans türüdür.

Daha kesin olarak, bir değerin kümülatif bağıl frekansı , değerin kendisinin bağıl frekansı artı tüm küçük değerlerin bağıl frekanslarının toplamına eşittir.

Kümülatif bağıl frekansın nasıl elde edildiğini görebilmeniz için, ilk örnekteki veri kümesinin kümülatif bağıl frekansı aşağıda hesaplanmıştır: