Gruplandırılmış veriler için çeyrekler nasıl hesaplanır?
Çeyrekler, bir veri kümesini dört eşit parçaya bölen değerlerdir.
Gruplandırılmış verilere ilişkin çeyrekleri hesaplamak için aşağıdaki formülü kullanabilirsiniz:
Q ben = L + (C/F) * (iN/4 – M)
Altın:
- L : i . çeyreği içeren aralığın alt sınırı
- C : Sınıfın genişliği
- F : i . çeyreği içeren aralığın frekansı
- N : Toplam frekans
- M : i’inci çeyreği içeren aralığa giden kümülatif frekans
Aşağıdaki örnekte bu formülün pratikte nasıl kullanılacağı gösterilmektedir.
Örnek: Gruplandırılmış veriler için çeyrekleri hesaplama
Aşağıdaki frekans dağılımına sahip olduğumuzu varsayalım:
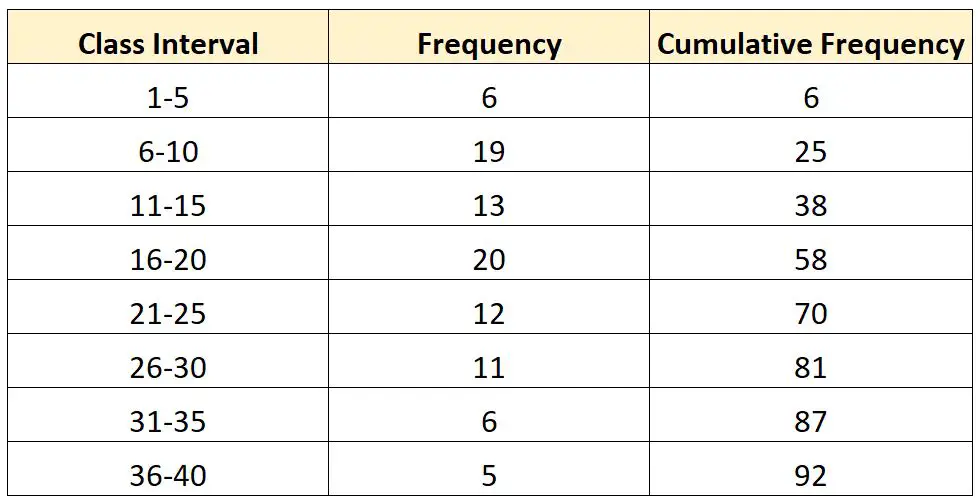
Şimdi bu dağılımın üçüncü çeyreğindeki (Q 3 ) değeri hesaplamak istediğimizi varsayalım.
Üçüncü çeyrekteki değer dağılımda (iN/4) konumunda yer alacaktır.
Yani (iN/4) = (3*92/4) = 69.
Üçüncü çeyreği içeren aralık 21-25 aralığı olacaktır çünkü 69, 58 ile 70’in kümülatif frekansları arasında yer alır.
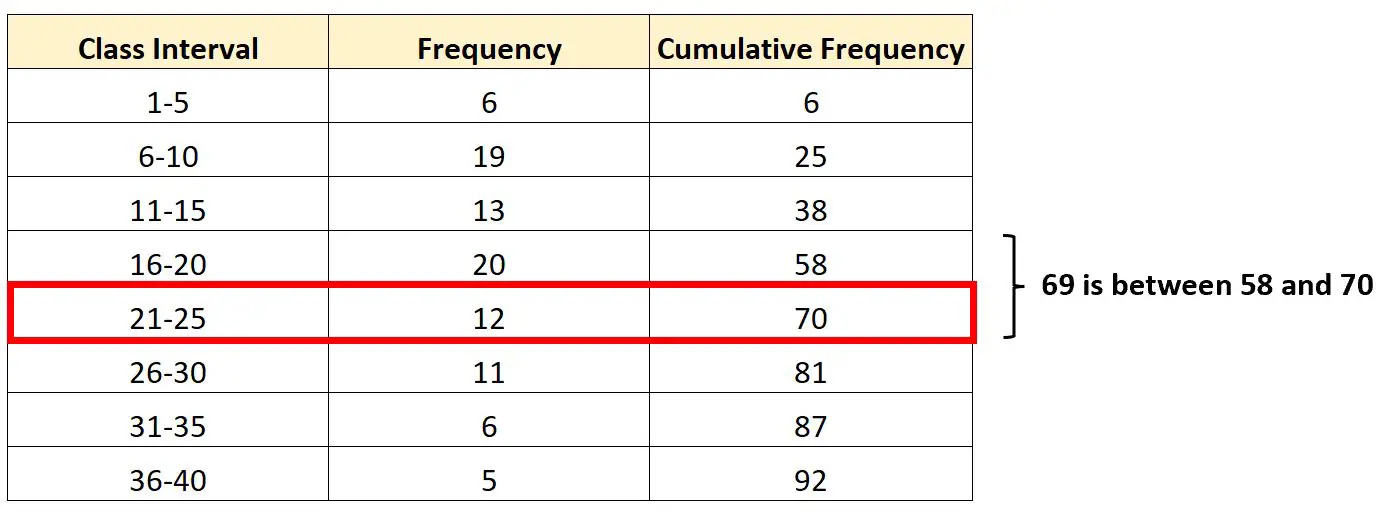
Bunu bilerek formülümüze eklemek için gerekli değerlerin her birini bulabiliriz:
L : i . çeyreği içeren aralığın alt sınırı
- Aralığın alt sınırı 21’dir .
C : Sınıfın genişliği
- Sınıfın genişliği şu şekilde hesaplanır: 25 – 21 = 4 .
F : i . çeyreği içeren aralığın frekansı
- 21-25 sınıfının frekansı 12’dir
N : Toplam frekans
- Tablodaki toplam kümülatif frekans 92’dir .
M : i’inci çeyreği içeren aralığa giden kümülatif frekans
- Sınıf 21-25’e kadar kümülatif frekans 58’dir .
Daha sonra üçüncü çeyrekteki değeri bulmak için tüm bu değerleri önceki formüle yerleştirebiliriz:
- Q ben = L + (C/F) * (iN/4 – M)
- Soru 3 = 21 + (4/12) * ((3)(92)/4 – 58)
- Ç3 = 24,67
Üçüncü çeyrekteki değer 24,67’dir .
Birinci ve ikinci çeyrek değerlerini hesaplamak için benzer bir yaklaşım kullanabilirsiniz.
Ek kaynaklar
Aşağıdaki eğitimler gruplandırılmış verilerle çalışma hakkında ek bilgi sağlar:
Gruplandırılmış verilerin ortalamasını ve standart sapmasını bulma
Gruplandırılmış veri modunu bulma
Gruplandırılmış verilerin medyanı nasıl bulunur?
Gruplanmış veya gruplanmamış frekans dağılımları
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil