Gruplandırılmış verilerin medyanı nasıl bulunur: örneklerle

Çoğu zaman bir şekilde bir arada gruplanan verilerin medyanını hesaplamak isteriz.

Tüm değerler en küçükten en büyüğe sıralandığında medyanın , bir veri kümesinin doğrudan ortasında yer alan değeri temsil ettiğini hatırlayın.

Örneğin, aşağıdaki gruplandırılmış verilere sahip olduğumuzu varsayalım:

Ham veri değerlerini bilmediğimiz için tam medyanı hesaplamak mümkün olmasa da aşağıdaki formülü kullanarak medyanı tahmin etmek mümkündür:

Gruplandırılmış verilerin medyanı = L + W[(N/2 – C) / F]

Altın:

• L : Medyan sınıfın alt sınırı
• W : Medyan sınıf genişliği
• N : Toplam frekans
• C : Medyan sınıfına kadar kümülatif frekans
• F : Medyan sınıf frekansı

Not : Orta sınıf, N/2’de yer alan değeri içeren sınıftır. Yukarıdaki örnekte N = 23 toplam değer vardır. Dolayısıyla medyan değeri 23/2 = 11,5 konumunda olup 21-30 sınıfındadır.

Aşağıdaki örnekler, farklı senaryolarda gruplandırılmış verilerin medyanının nasıl hesaplanacağını gösterir.

Örnek 1: Gruplandırılmış Verilerin Medyanını Hesaplama

Belirli bir sınıftaki 40 öğrencinin not verdiği sınavı gösteren aşağıdaki frekans dağılımına sahip olduğumuzu varsayalım:

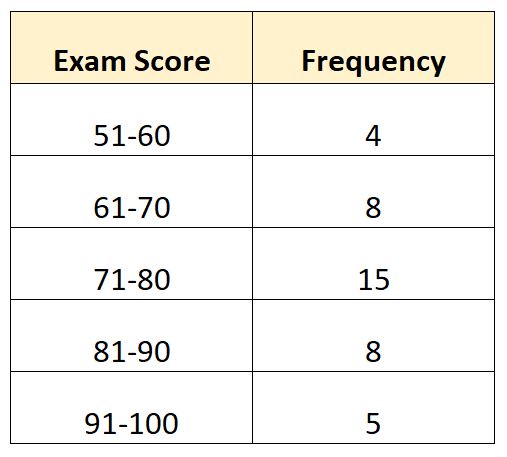
Bu örnekte N = 40 toplam değer vardır. Yani medyan değeri 40/2=20’nin bulunduğu sınıftadır. 20. en büyük değer 71-80 sınıfında olacaktır.

Bunu bilerek aşağıdaki değerleri hesaplayabiliriz:

• L : Alt orta sınıf sınırı: 71
• W : Medyan sınıf genişliği: 9
• N : Toplam frekans: 40
• C : Medyan sınıfa kadar kümülatif frekans: 12
• F : Medyan sınıf frekansı: 15

Dağılımın medyanını hesaplamak için bu değerleri formüle ekleyebiliriz:

• Medyan = L + W[(N/2 – C) / F]
• Medyan = 71 + 9[(40/2 – 12) / 15]
• Medyan = 75,8

Ortalama sınav puanının 75,8 olduğunu tahmin ediyoruz.

Örnek 2: Gruplandırılmış Verilerin Medyanını Hesaplama

60 basketbolcunun maç başına attığı sayıyı gösteren aşağıdaki frekans dağılımına sahip olduğumuzu varsayalım:

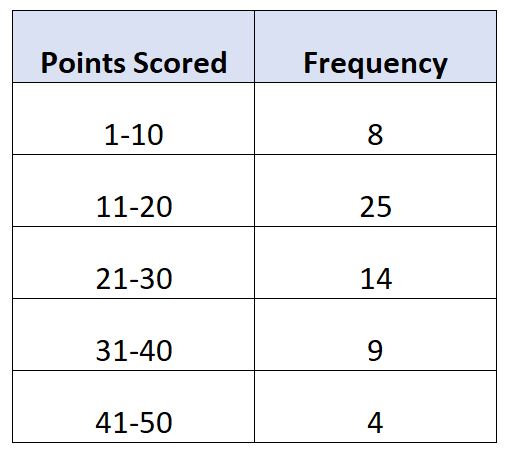
Bu örnekte N = 60 toplam değer vardır. Yani medyan değeri 60/2=30’un yer aldığı sınıfta yer almaktadır. 30’uncu en büyük değer 11-20 sınıfında olacaktır.

Bunu bilerek aşağıdaki değerleri hesaplayabiliriz:

• L : Alt orta sınıf sınırı: 11
• W : Medyan sınıf genişliği: 9
• N : Toplam frekans: 60
• C : Medyan sınıfa kadar kümülatif frekans: 8
• F : Medyan sınıf frekansı: 25

Dağılımın medyanını hesaplamak için bu değerleri formüle ekleyebiliriz:

• Medyan = L + W[(N/2 – C) / F]
• Medyan = 11 + 9[(60/2 – 8) / 25]
• Medyan = 18,92

Ortalama sınav puanının 18,92 olacağını tahmin ediyoruz.

Ek kaynaklar

Aşağıdaki eğitimlerde gruplandırılmış verilerle diğer ortak işlemlerin nasıl gerçekleştirileceği açıklanmaktadır:

Gruplandırılmış verilerin ortalamasını ve standart sapmasını bulma
Gruplandırılmış veri modunu bulma
Gruplandırılmış veriler için yüzdelik sıralama nasıl hesaplanır?