Gruplandırılmış verilerin varyansı nasıl bulunur (örnekle)

Genellikle gruplandırılmış bir frekans dağılımının varyansını hesaplamak isteriz.

Örneğin, aşağıdaki gruplandırılmış frekans dağılımına sahip olduğumuzu varsayalım:

Ham veri değerlerini bilmediğimiz için varyansı tam olarak hesaplamak mümkün olmasa da aşağıdaki formülü kullanarak varyansı tahmin etmek mümkündür:

Varyans: Σn _i ( _mi -μ) ² / (N-1)

Altın:

• n _i : ^i’inci grubun frekansı
• _mi : ^i’inci grubun ortası
• μ : Ortalama
• N: Toplam örneklem büyüklüğü

Not: Her grubun orta noktası, aralığın alt ve üst değerlerinin ortalaması alınarak bulunabilir. Örneğin birinci grubun orta noktası şu şekilde hesaplanır: (1+10) / 2 = 5,5.

Aşağıdaki örnekte bu formülün pratikte nasıl kullanılacağı gösterilmektedir.

Örnek: Gruplandırılmış verilerin varyansını hesaplama

Aşağıdaki gruplandırılmış verilere sahip olduğumuzu varsayalım:

Bu gruplandırılmış verilerin varyansını hesaplamak için daha önce bahsedilen formülü şu şekilde kullanacağız:

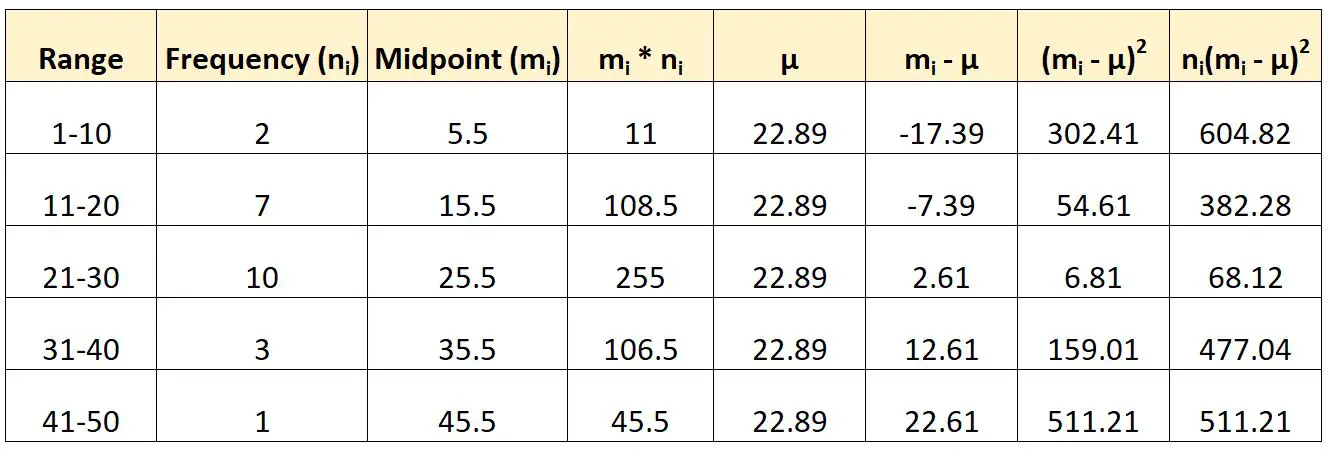
Daha sonra varyansı şu şekilde hesaplayacağız:

• Varyans: Σn _i ( _mi -μ) ² / (N-1)
• Fark : (604,82 + 382,28 + 68,12 + 477,04 + 511,21) / (23-1)
• Fark : 92.885

Veri setinin varyansı 92,885 olarak çıkıyor.

Ek kaynaklar

Aşağıdaki eğitimlerde gruplandırılmış veriler için diğer ölçümlerin nasıl hesaplanacağı açıklanmaktadır:

Gruplandırılmış verilerin ortalamasını ve standart sapmasını bulma
Gruplandırılmış veriler için yüzdelik sıralama nasıl hesaplanır?
Gruplandırılmış verilerin medyanı nasıl bulunur?
Gruplandırılmış veri modunu bulma