Lognormal dağılım

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makalede istatistikte lognormal dağılımın ne olduğu açıklanmaktadır. Böylece lognormal dağılımın özelliklerinin neler olduğunu ve bu tür olasılık dağılımının grafiğini öğreneceksiniz.

Lognormal dağılım nedir?

Lognormal dağılım veya lognormal dağılım , logaritması normal dağılıma uyan rastgele bir değişkeni tanımlayan bir olasılık dağılımıdır.

Bu nedenle, eğer X değişkeni normal dağılıma sahipse, üstel fonksiyon e ^x lognormal dağılıma sahiptir.

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Logaritmanın yalnızca bir pozitif argüman alan bir fonksiyon olması nedeniyle lognormal dağılımın yalnızca değişken değerleri pozitif olduğunda kullanılabileceğini unutmayın.

Lognormal dağılımın istatistikteki farklı uygulamaları arasında, bu dağılımın finansal yatırımları analiz etmek ve güvenilirlik analizleri yapmak için kullanılmasını öne çıkarıyoruz.

Lognormal dağılım aynı zamanda Tinaut dağılımı olarak da bilinir ve bazen lognormal dağılım veya log-normal dağılım olarak da yazılır.

Lognormal dağılım grafiği

Artık lognormal dağılımın tanımını bildiğimize göre, bu bölümde lognormal dağılımın grafiksel gösteriminin, aritmetik ortalamasına ve standart sapmasına bağlı olarak nasıl değiştiğini göreceğiz.

Lognormal dağılımın yoğunluk fonksiyonunun grafiği aşağıdaki gibidir:

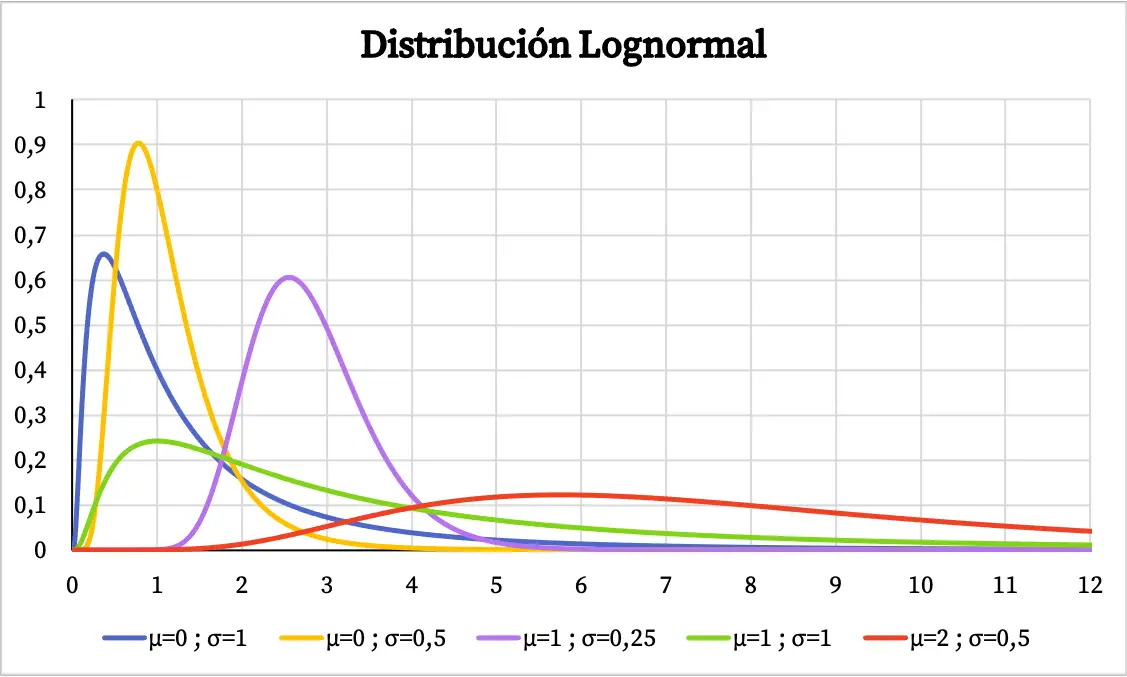
Öte yandan lognormal dağılımın kümülatif olasılık grafiği şu şekildedir:

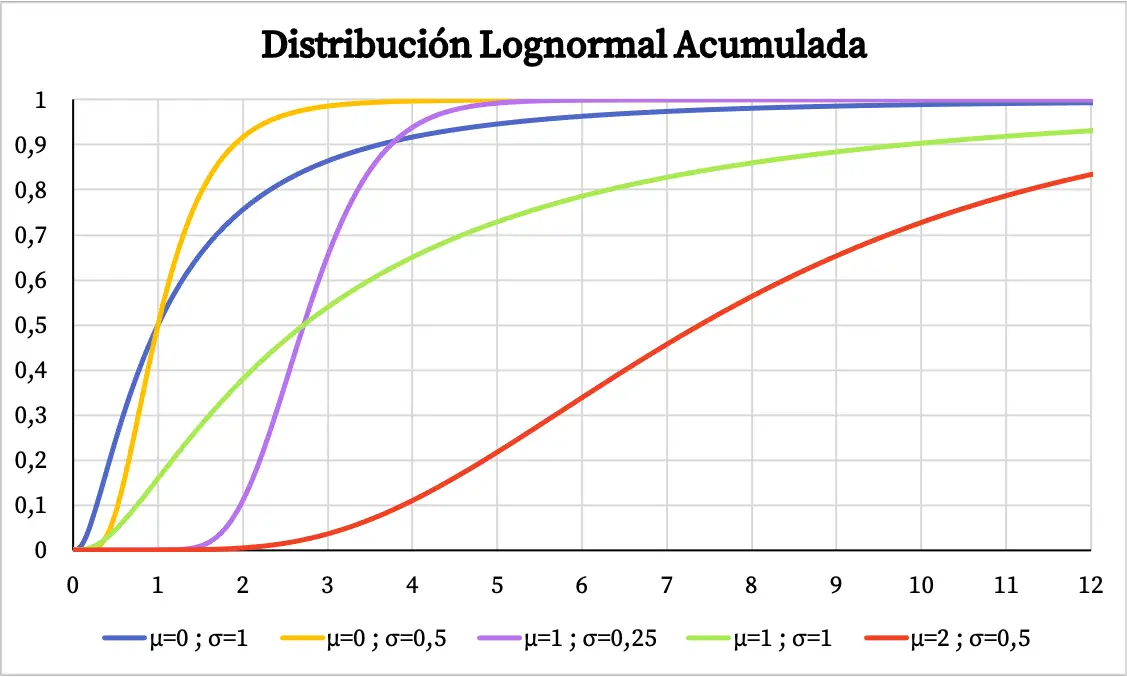
Lognormal dağılımın özellikleri

Lognormal dağılım aşağıdaki özelliklere sahiptir:

Lognormal dağılım iki parametrenin değeriyle tanımlanır: aritmetik ortalaması μ ve varyansı σ ² .

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Logaritmanın negatif veya sıfır değerleri kabul etmemesi nedeniyle lognormal dağılımın alanı pozitif gerçek sayılardan oluşur.

$x\in (0,+\infty)$

Lognormal dağılım beklentisi, e sayısının ortalamanın toplamı artı varyansın ikiye bölünmesine eşittir.

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

Öte yandan lognormal dağılımın varyansı aşağıdaki ifadeyle hesaplanabilir:

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

Lognormal dağılımın modu, dağılımın ortalamasına yükseltilen e sayısına eşdeğerdir.

$Mo=e^\mu$

Lognormal dağılımın çarpıklık katsayısı aşağıdaki formül uygulanarak belirlenebilir:

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

Lognormal dağılımın yoğunluk fonksiyonunun formülü şöyledir:

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

Lognormal dağılımın kümülatif olasılık fonksiyonunun formülü şöyledir:

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

Altın

$\Phi$

standart normal dağılımın kümülatif olasılık fonksiyonudur.

Lognormal dağılımın aritmetik ortalaması, medyanın değerinden daha büyüktür.

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

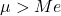
yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Lognormal dağılım nedir?

Lognormal dağılım grafiği

Lognormal dağılımın özellikleri

yazar hakkında

Dr.benjamin anderson

Yorum ekle