Google e-tablolarda güven aralıkları nasıl hesaplanır?

Bir ortalama için güven aralığı, belirli bir güven düzeyine sahip bir popülasyon ortalamasını içermesi muhtemel bir değer aralığıdır.

Aşağıdaki şekilde hesaplanır:

Güven aralığı = x +/- t*(s/√ n )

Altın:

• x : örnek ortalama
• t: güven düzeyine karşılık gelen t değeri
• s: numune standart sapması
• n: örneklem büyüklüğü

Bu eğitimde Google E-Tablolar’da güven aralıklarının nasıl hesaplanacağı açıklanmaktadır.

T dağılımını kullanan güven aralıkları

Küçük bir örneklemle (n < 30) çalışıyorsak, popülasyon ortalaması için güven aralığını hesaplamak amacıyla t dağılımını kullanabiliriz.

Örneğin, 15 bitkiden oluşan bir örnek kullanarak belirli bir bitki türünün gerçek ortalama popülasyon yüksekliği (inç cinsinden) için bir güven aralığı hesaplamak istediğimizi varsayalım:

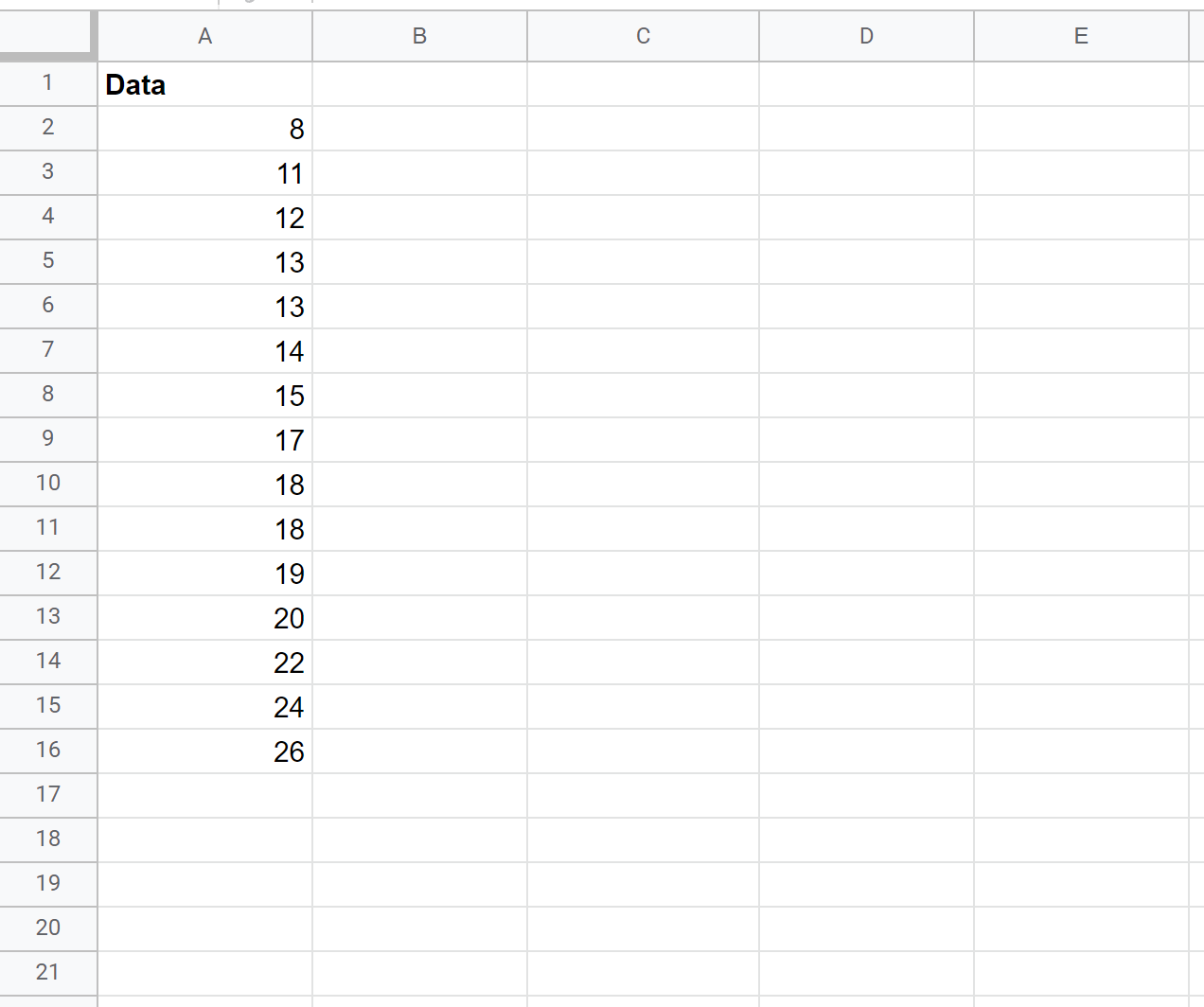
İlk olarak örneklem ortalamasını, örneklem standart sapmasını ve örneklem büyüklüğünü hesaplayabiliriz:

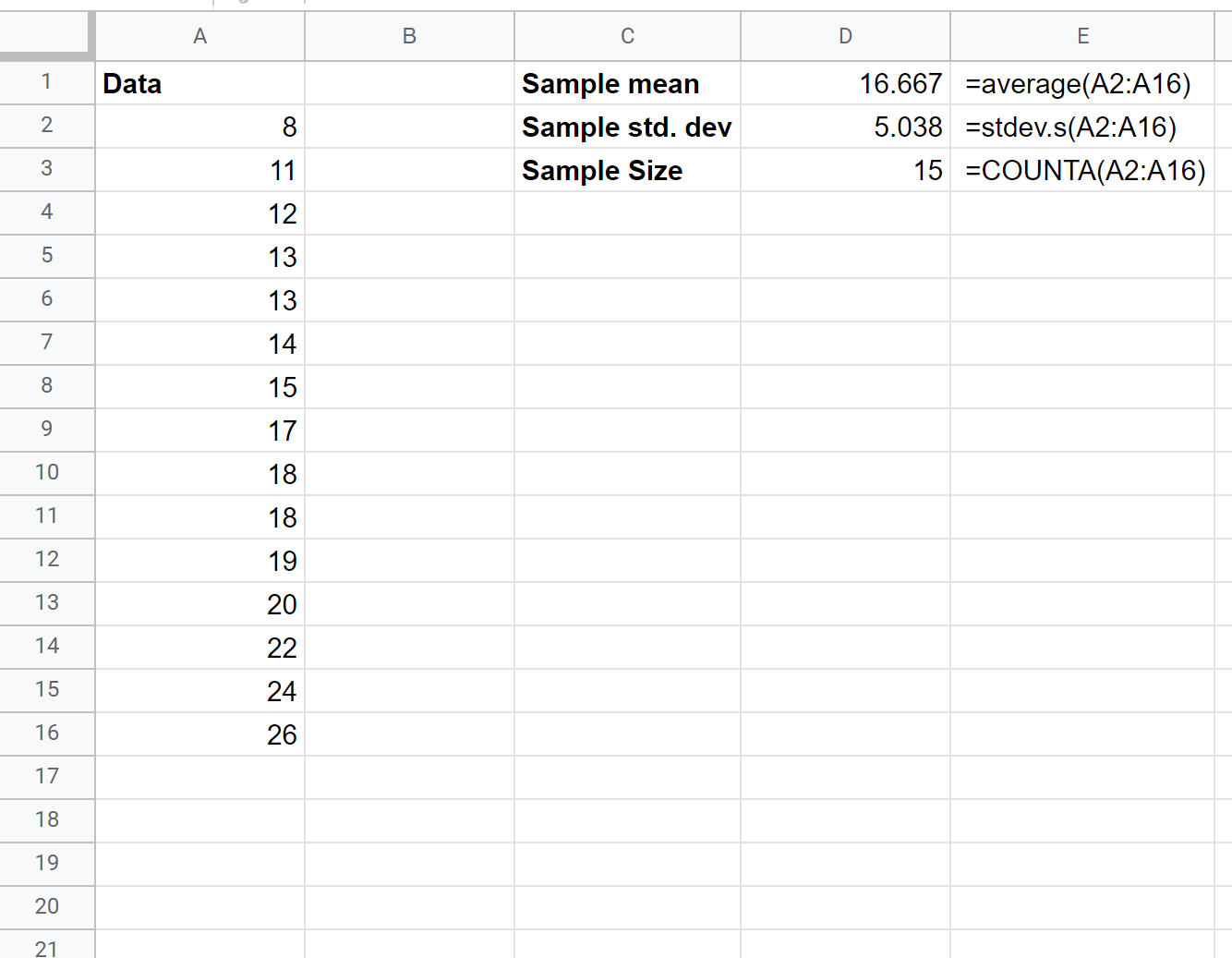
Daha sonra %95 güven aralığının alt ve üst sınırını hesaplamak için aşağıdaki formülleri kullanabiliriz:

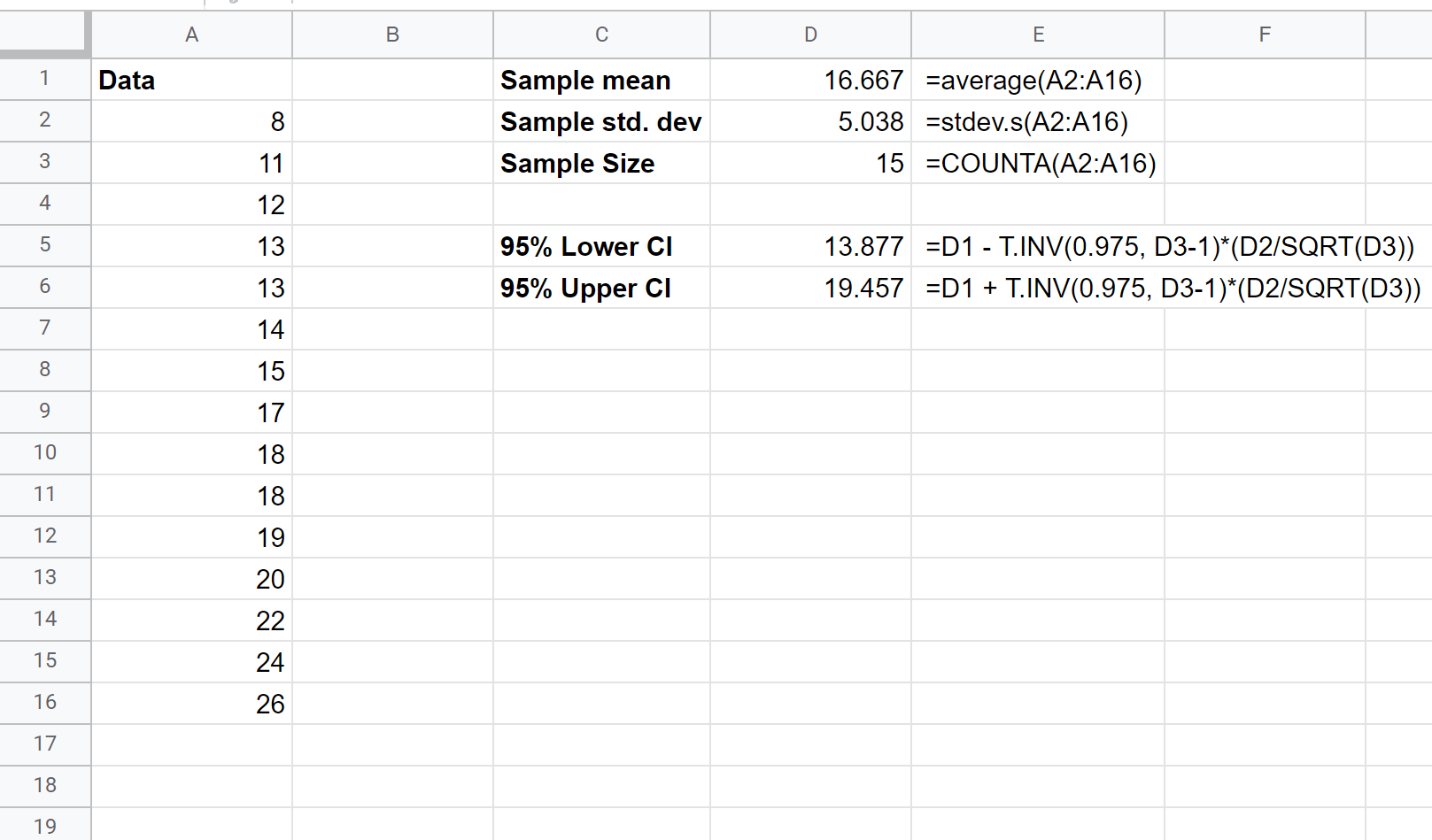
Gerçek ortalama popülasyon büyüklüğü için %95 güven aralığı (13.877, 19.457)’ dir.

Normal dağılım kullanılarak güven aralıkları

Daha büyük örneklerle (n≥30) çalışırsak, merkezi limit teoremi sayesinde örnek ortalamasının örnekleme dağılımının normal dağıldığını varsayabiliriz.

Bu, güven aralığı için kullanılacak kritik değeri hesaplamak için NORM.S.INV() işlevini kullanabileceğimiz anlamına gelir.

Aşağıdaki örnek, 30 bitkiden oluşan bir örnek kullanılarak belirli bir bitki türünün gerçek ortalama popülasyon yüksekliğine (inç cinsinden) ilişkin güven aralığının nasıl hesaplanacağını gösterir:

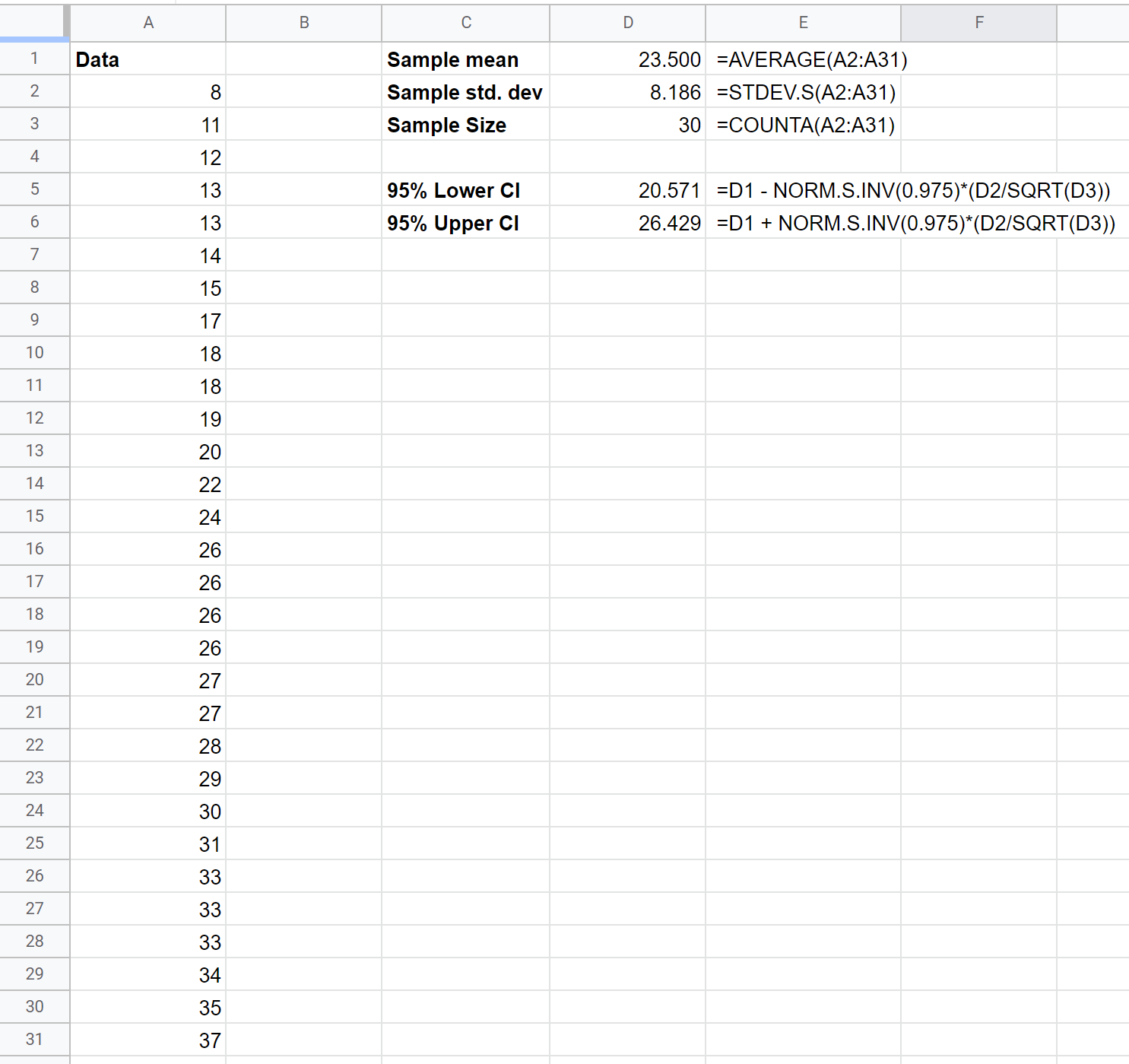
Gerçek ortalama popülasyon büyüklüğü için %95 güven aralığı (20,571, 26,429)’ dir.

Daha yüksek güven seviyelerinin daha geniş güven aralıklarına yol açtığını unutmayın. Örneğin, tam olarak aynı veriler için %99 GA’nın nasıl hesaplanacağı aşağıda açıklanmıştır:

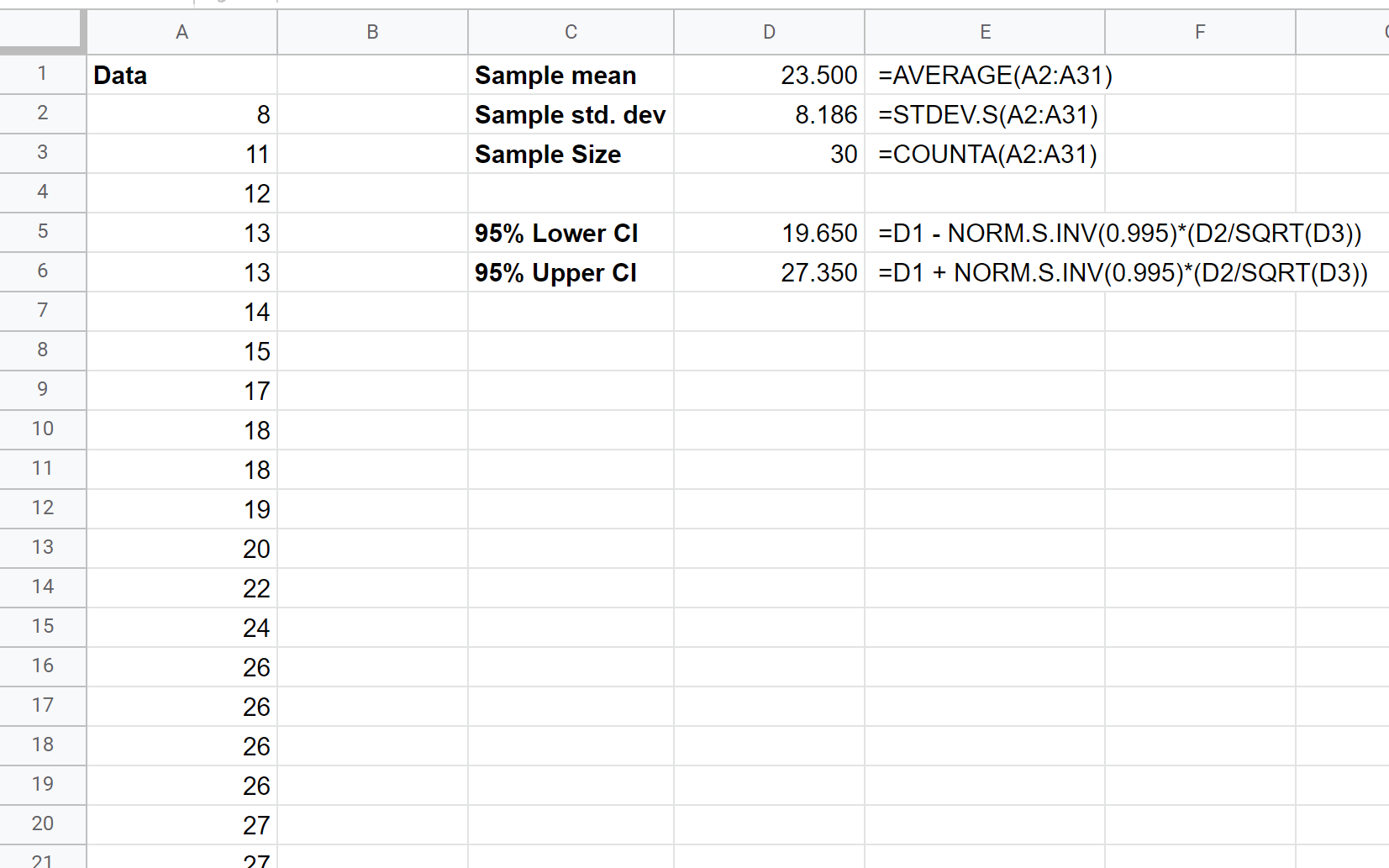
Gerçek ortalama popülasyon büyüklüğü için %99 güven aralığı (19.650, 27.350)’ dir.

Bu %99 güven aralığının daha önce hesapladığımız %95 güven aralığından daha geniş olduğunu unutmayın.

İlgili: Güven Düzeyi vs. Güven Aralığı: Fark Nedir?

Ek kaynaklar

Aşağıdaki eğitimler, diğer istatistiksel yazılımları kullanarak güven aralıklarının nasıl hesaplanacağını açıklamaktadır:

Excel’de Güven Aralıkları Nasıl Hesaplanır?
R’de güven aralıkları nasıl hesaplanır
Python’da güven aralıkları nasıl hesaplanır