Excel'de güven aralıkları nasıl hesaplanır?
Güven aralığı, belirli bir güven düzeyine sahip bir popülasyon parametresini içermesi muhtemel bir değer aralığıdır. Aşağıdaki genel formüle göre hesaplanır:
Güven aralığı = (nokta tahmini) +/- (kritik değer)* (standart hata)
Bu formül, muhtemelen bir miktar güven düzeyine sahip bir popülasyon parametresi içeren, alt sınırı ve üst sınırı olan bir aralık oluşturur:
Güven aralığı = [alt sınır, üst sınır]
Bu eğitimde Excel’de aşağıdaki güven aralıklarının nasıl hesaplanacağı açıklanmaktadır:
1. Ortalama için güven aralığı
2. Ortalamalar arasındaki fark için güven aralığı
3. Bir orantı için güven aralığı
4. Oranlar arasındaki fark için güven aralığı
Hadi gidelim!
Örnek 1: Bir ortalama için güven aralığı
Bir ortalamanın güven aralığını hesaplamak için aşağıdaki formülü kullanırız:
Güven aralığı = x +/- z*(s/√n)
Altın:
- x : örnek ortalama
- z: seçilen z değeri
- s: numune standart sapması
- n: örneklem büyüklüğü
Örnek: Aşağıdaki bilgileri içeren rastgele bir kaplumbağa örneği topladığımızı varsayalım:
- Örneklem büyüklüğü n = 25
- Ortalama numune ağırlığı x = 300
- Örneklem standart sapması s = 18,5
Aşağıdaki ekran görüntüsü kaplumbağa popülasyonunun gerçek ortalama ağırlığı için %95 güven aralığının nasıl hesaplanacağını gösterir:
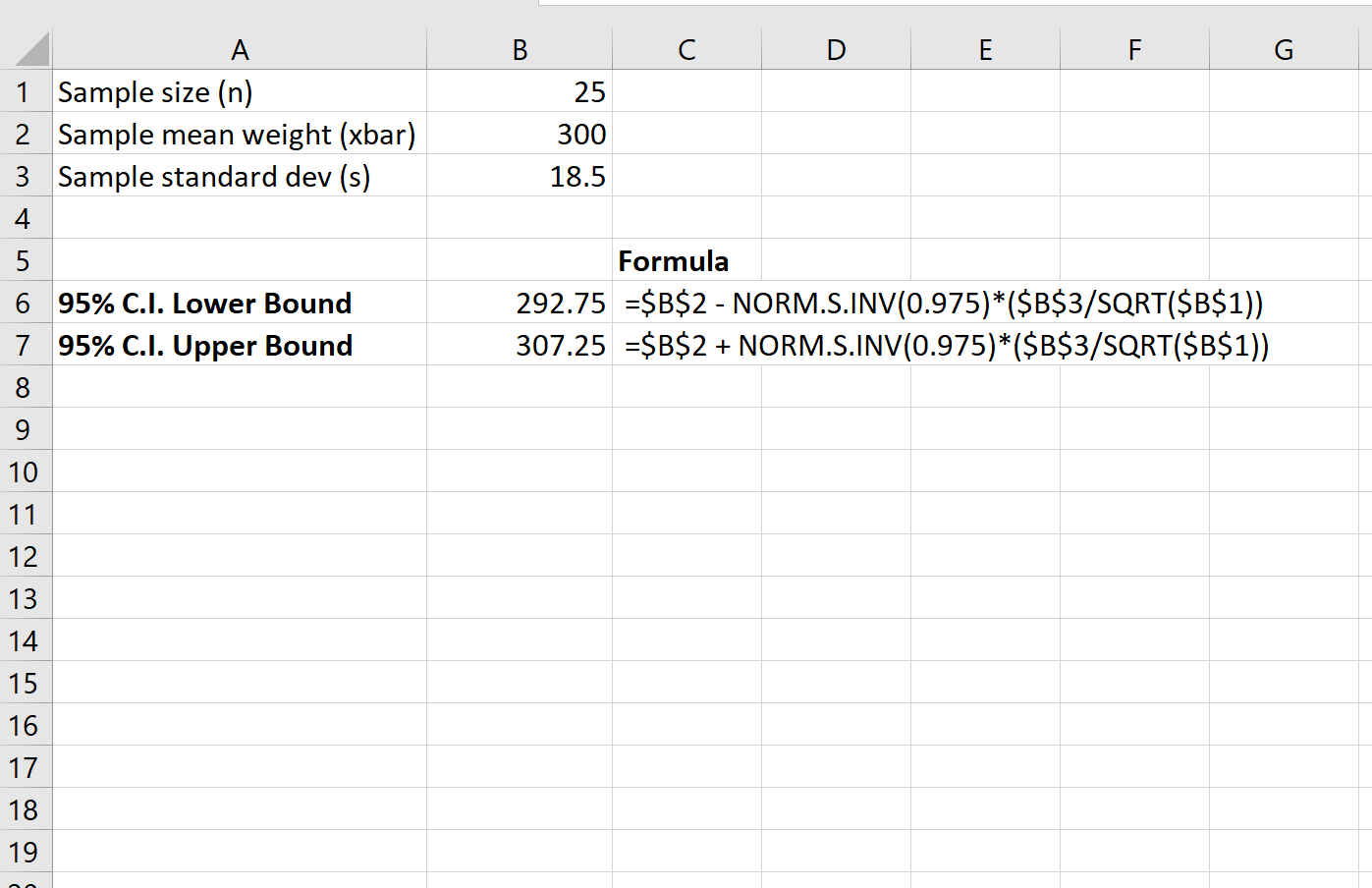
Gerçek ortalama kaplumbağa popülasyonu ağırlığı için %95 güven aralığı [292,75, 307,25]’ tir.
Örnek 2: Ortalamalar arasındaki fark için güven aralığı
Nüfus ortalamalarındaki farka ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanırız:
Güven aralığı = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Altın:
- x 1 , x 2 : örnek 1’in ortalaması, örnek 2’nin ortalaması
- t: güven düzeyine ve (n 1 + n 2 -2) serbestlik derecesine dayalı t-kritik değeri
- sp 2 : birleştirilmiş varyans, şu şekilde hesaplanır: ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t: t-kritik değeri
- n 1 , n 2 : örneklem büyüklüğü 1, örneklem büyüklüğü 2
Örnek: İki farklı kaplumbağa türü arasındaki ortalama ağırlık farkını tahmin etmek istediğimizi varsayalım. Bu nedenle her popülasyondan rastgele 15 kaplumbağa örneği topluyoruz. Her numunenin özet verileri aşağıda verilmiştir:
Örnek 1:
- x1 = 310
- 1 = 18,5
- n1 = 15
Örnek 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
Aşağıdaki ekran görüntüsü popülasyon ortalamalarındaki gerçek fark için %95 güven aralığının nasıl hesaplanacağını gösterir:
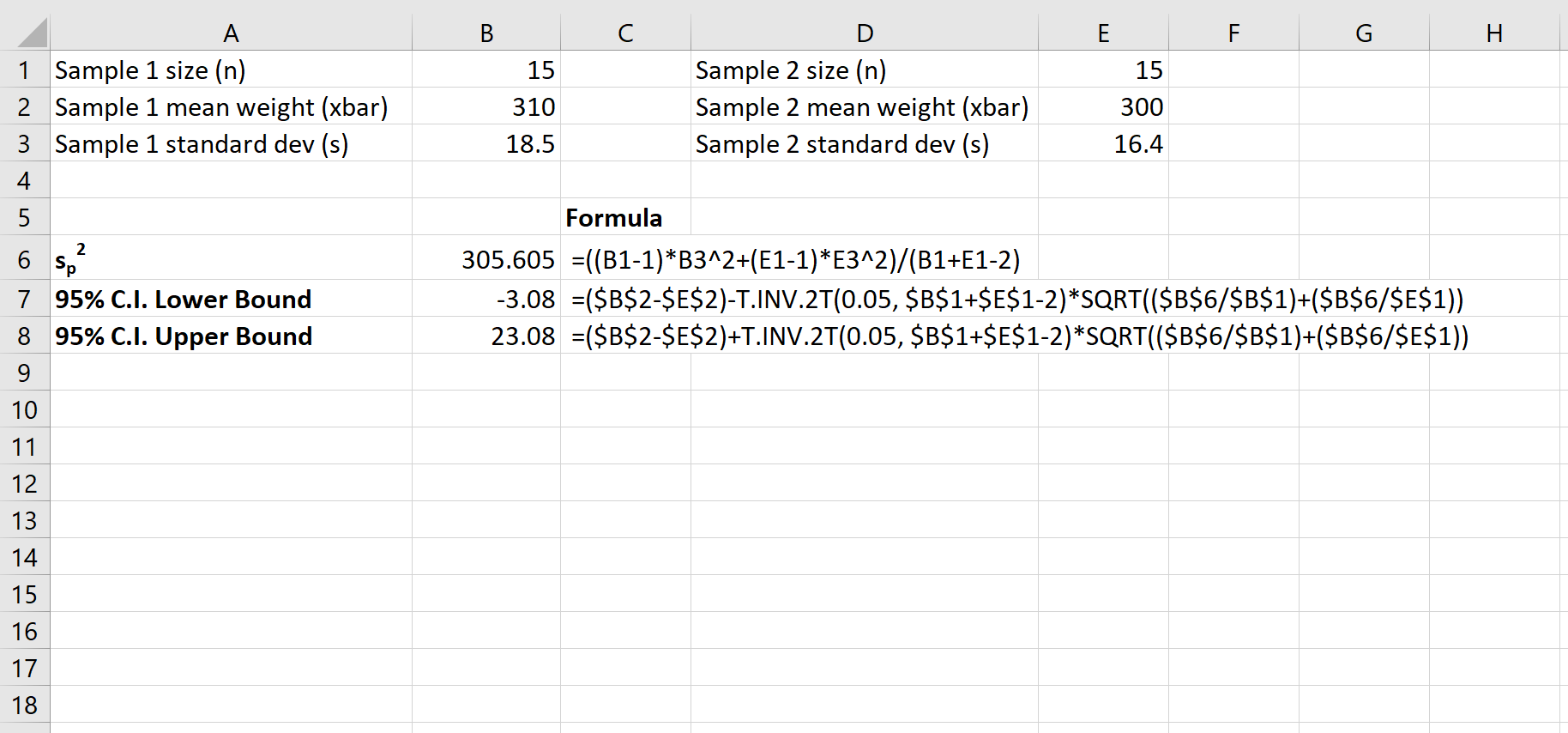
Popülasyon ortalamaları arasındaki gerçek fark için %95 güven aralığı [-3,08, 23,08]’ dir.
Örnek 3: Bir orantı için güven aralığı
Bir orana ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanırız:
Güven aralığı = p +/- z*√ p(1-p) / n
Altın:
- p: örnek oranı
- z: seçilen z değeri
- n: örneklem büyüklüğü
Örnek: Bir ilçede belirli bir yasayı destekleyen sakinlerin oranını tahmin etmek istediğimizi varsayalım. 100 sakinden rastgele bir örnek seçiyoruz ve onlara yasadaki konumlarının ne olduğunu soruyoruz. Sonuçlar burada:
- Örneklem büyüklüğü n = 100
- Kanun lehine oran p = 0,56
Aşağıdaki ekran görüntüsü, eyalet çapında yasayı destekleyen sakinlerin gerçek oranı için %95 güven aralığının nasıl hesaplanacağını göstermektedir:
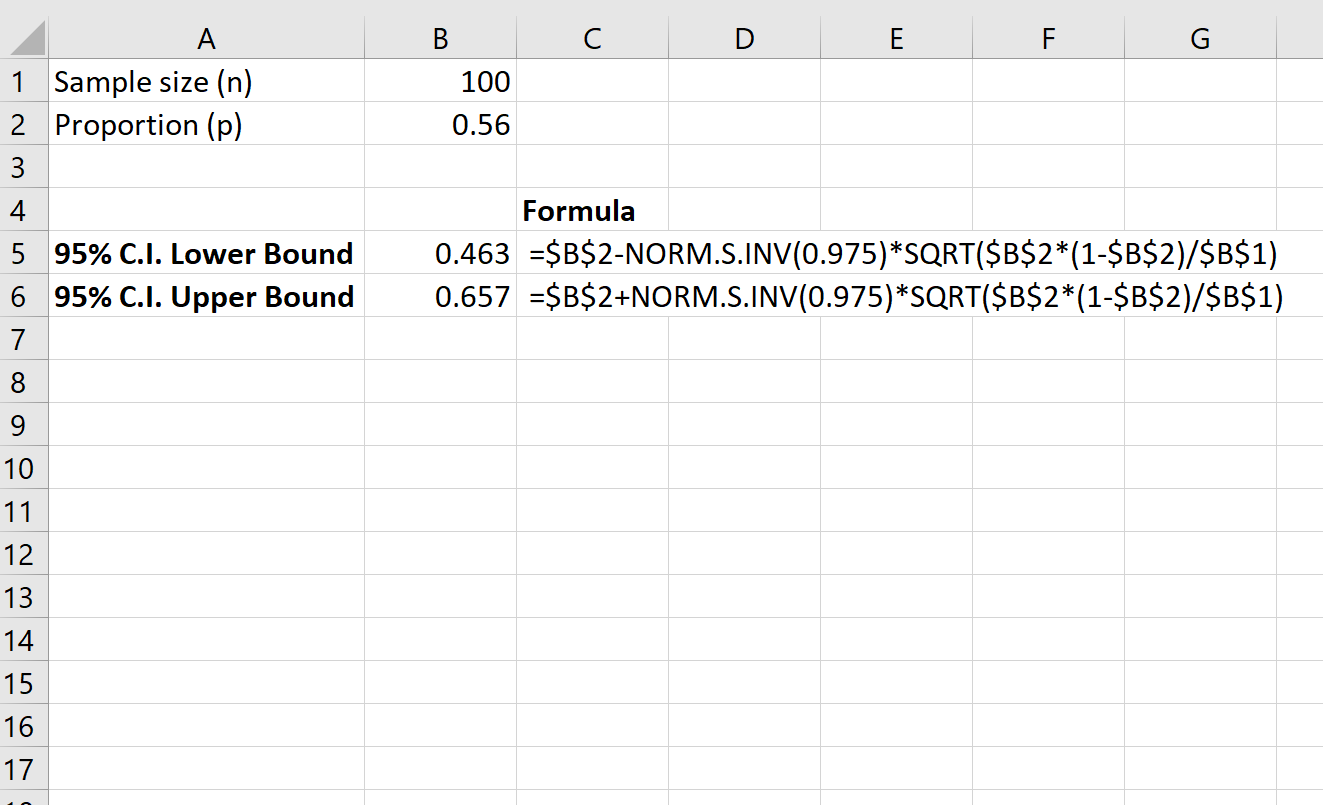
Eyalet genelinde yasayı destekleyen sakinlerin gerçek oranı için %95 güven aralığı [0,463, 0,657]’ dir.
Örnek 4: Oranlardaki fark için güven aralığı
Oranlardaki farka ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanırız:
Güven aralığı = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Altın:
- p 1 , p 2 : 1. numunenin oranı, 2. numunenin oranı
- z: güven düzeyine dayalı z-kritik değeri
- n 1 , n 2 : örneklem büyüklüğü 1, örneklem büyüklüğü 2
Örnek: A İlçesinde belirli bir yasayı destekleyen sakinlerin oranı ile B İlçesindeki yasayı destekleyen sakinlerin oranı arasındaki farkı tahmin etmek istediğimizi varsayalım. Her örnek için özet veriler aşağıda verilmiştir:
Örnek 1:
- n1 = 100
- p 1 = 0,62 (yani 100 kişiden 62’si yasayı destekliyor)
Örnek 2:
- n2 = 100
- p 2 = 0,46 (yani 100 kişiden 46’sı yasayı destekliyor)
Aşağıdaki ekran görüntüsü, ilçeler arasında yasayı destekleyen sakinlerin oranındaki gerçek fark için %95 güven aralığının nasıl hesaplanacağını göstermektedir:
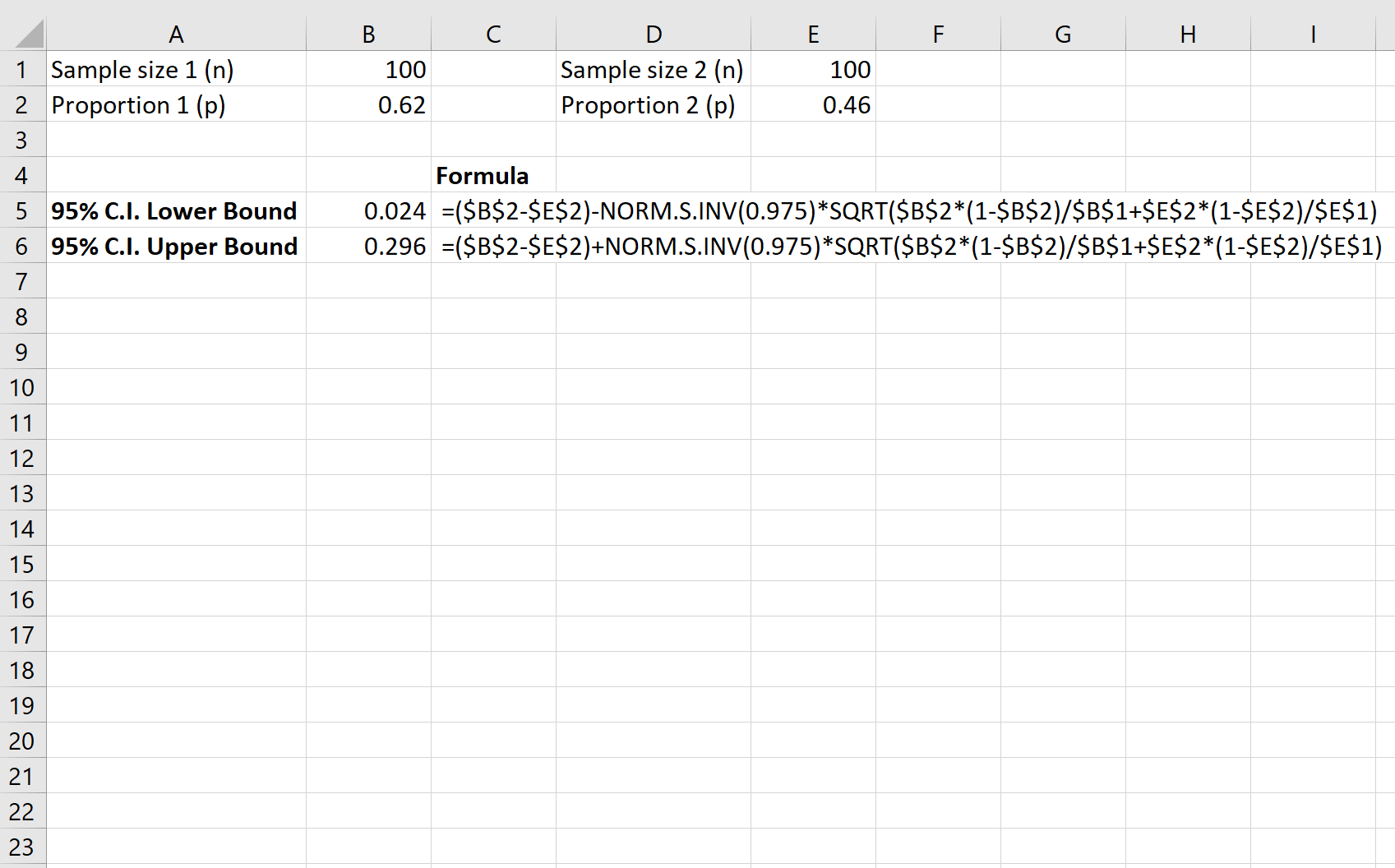
İlçeler arasında yasayı destekleyen sakinlerin oranındaki gerçek fark için %9,5 güven aralığı [0,024, 0,296]’ dır.
Daha fazla Excel eğitimini burada bulabilirsiniz.
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil