Ancova'ya giriş (varyans analizi)

ANCOVA “kovaryans analizi” anlamına gelir. Bir ANCOVA’nın nasıl çalıştığını anlamak için öncelikle ANOVA’yı anlamak yardımcı olur.

Bir ANOVA   (Varyans analizi) üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için kullanılır.

Örneğin, çalışma tekniğinin bir sınıftaki öğrencilerin sınav puanlarını etkileyip etkilemediğini bilmek istediğimizi varsayalım. Sınıfı rastgele üç gruba ayırdık. Her grup bir sınava hazırlanmak için bir ay boyunca farklı bir çalışma tekniği kullanır. Ay sonunda tüm öğrenciler aynı sınava girerler.

Çalışma tekniğinin sınav puanları üzerinde etkisi olup olmadığını öğrenmek için tek yönlü bir ANOVA gerçekleştirebiliriz; bu bize üç grubun ortalama puanları arasında istatistiksel olarak anlamlı bir fark olup olmadığını söyleyecektir.

ANCOVA, bir veya daha fazla ortak değişkeni hesaba kattıktan sonra üç veya daha fazla bağımsız grup arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek istediğimiz ANOVA’nın bir uzantısıdır.

Ortak değişken , yanıt değişkenine göre değişen sürekli bir değişkendir.

Örneğin ders çalışma tekniğinin sınav puanlarına etkisinin olup olmadığını bilmek istiyoruz ancak öğrencinin halihazırda sınıfta aldığı notu da hesaba katmak istiyoruz . Mevcut notlarını ortak değişken olarak kullanabilir ve ANCOVA yaparak üç grubun ortalama sınav puanları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirleyebiliriz.

Bu, ortak değişkenin etkisi ortadan kaldırıldığında çalışma tekniğinin sınav puanları üzerinde bir etkisi olup olmadığını test etmemize olanak tanır.

Dolayısıyla, eğer üç çalışma tekniği arasında sınav puanları arasında istatistiksel olarak anlamlı bir fark olduğunu bulursak, bu farkın öğrencilerin sınıftaki mevcut notu dikkate alındıktan sonra bile var olduğundan emin olabiliriz (c ‘yani, eğer zaten iyi durumdalar mı veya zaten iyi durumdalar mı?) sınıfta değil) .

ANCOVA varsayımları

ANCOVA gerçekleştirmeden önce aşağıdaki varsayımların karşılandığından emin olmak önemlidir:

• Ortak değişken(ler) ve faktör değişken(ler)i bağımsızdır – Ortak değişken ve faktör değişkeni birbirinden bağımsız olmalıdır, çünkü modele bir ortak değişken terimi eklemek yalnızca ortak değişken ve faktör değişkeni bağımsız olarak hareket ederse anlamlı olur. yanıt değişkeni
• Ortak değişken(ler) sürekli verilerdir. Ortak değişkenler sürekli olmalıdır (yani aralık veya oran verileri).
• Varyansların homojenliği – Gruplar arasındaki varyanslar yaklaşık olarak eşit olmalıdır.
• Bağımsızlık – Her gruptaki gözlemler bağımsız olmalıdır.
• Normallik – Veriler her grupta yaklaşık olarak normal şekilde dağıtılmalıdır.
• Aşırı uç değerler yok – Grupların hiçbirinde ANCOVA sonuçlarını önemli ölçüde etkileyebilecek aşırı uç değerler olmamalıdır.

ANCOVA: örnek

Bir öğretmen, üç farklı çalışma tekniğinin sınav puanlarını etkileyip etkilemediğini bilmek istiyor ancak öğrencinin halihazırda sınıfta aldığı notu da hesaba katmak istiyor.

Aşağıdaki değişkenleri kullanarak bir ANCOVA gerçekleştirecektir:

• Faktör değişkeni: teknik çalışma
• Ortak değişken: mevcut puan
• Yanıt değişkeni: sınav puanı

Aşağıdaki tabloda çalışmaya katılmak üzere seçilen 15 öğrencinin veri seti sunulmaktadır:

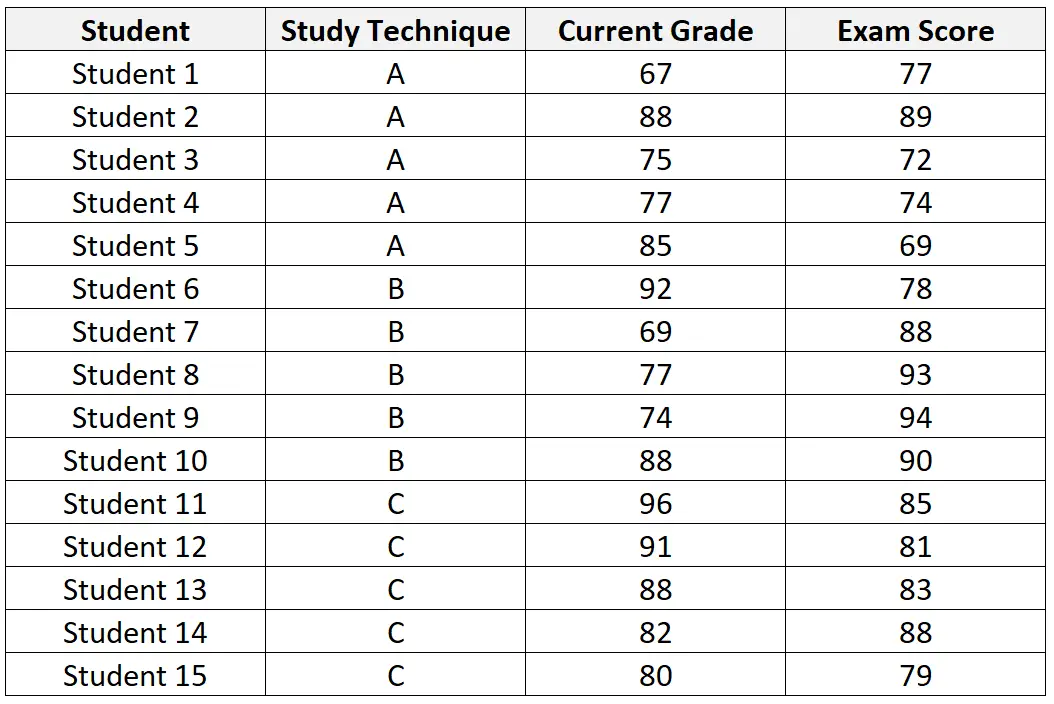
Veri seti üzerinde ANCOVA gerçekleştirdikten sonra öğretmen aşağıdaki sonuçları elde eder:

Çalışma tekniğinin p değeri 0,03155’tir . Bu değer 0,05’ten küçük olduğundan, öğrencinin sınıftaki mevcut notu hesaba katıldıktan sonra bile her çalışma tekniğinin aynı ortalama sınav notuna yol açtığı yönündeki sıfır hipotezini reddedebiliriz.

Hangi çalışma tekniklerinin farklı ortalama sınav puanları ürettiğini tam olarak belirlemek için öğretmenin post-hoc testler yapması gerekecektir.

Ek kaynaklar

Excel’de ANCOVA nasıl gerçekleştirilir
R’de ANCOVA nasıl gerçekleştirilir
Python’da ANCOVA nasıl gerçekleştirilir?
ANOVA, ANCOVA, MANOVA ve MANCOVA arasındaki farklar