Sas'ta iki oranlı z testi nasıl yapılır

İki nüfus oranı arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için iki oranlı z testi kullanılır.

Bu test aşağıdaki sıfır hipotezini kullanır:

• H ₀ : μ ₁ = μ ₂ (iki popülasyon oranı eşittir)

Alternatif hipotez iki taraflı, sol veya sağ olabilir:

• H ₁ (iki kuyruklu): π ₁ ≠ π ₂ (iki popülasyon oranı eşit değildir)
• H ₁ (solda): π ₁ < π ₂ (nüfus 1’in oranı, nüfus 2’nin oranından azdır)
• H ₁ (sağ): π ₁ > π ₂ (nüfus 1’in oranı, nüfus 2’nin oranından daha büyüktür)

Z testi istatistiğini hesaplamak için aşağıdaki formülü kullanırız:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

burada p ₁ ve p ₂ örnek oranlarıdır, n ₁ ve n ₂ örnek boyutlarıdır ve p aşağıdaki şekilde hesaplanan toplam havuzlanmış orandır:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

Z testi istatistiğine karşılık gelen p değeri seçilen anlamlılık seviyesinden küçükse (ortak seçenekler 0,10, 0,05 ve 0,01’dir), o zaman sıfır hipotezini reddedebilirsiniz.

Aşağıdaki örnek, SAS’ta iki oranlı z testinin nasıl gerçekleştirileceğini gösterir.

Örnek: SAS’ta İki Oranlı Z Testi

A İlçesinde belirli bir yasayı destekleyen sakinlerin oranı ile B İlçesinde yasayı destekleyen sakinlerin oranı arasında bir fark olup olmadığını bilmek istediğimizi varsayalım.

Bunu test etmek için her ilçeden rastgele 50 sakinden oluşan bir örnek topluyoruz ve kaçının yasayı desteklediğini sayıyoruz.

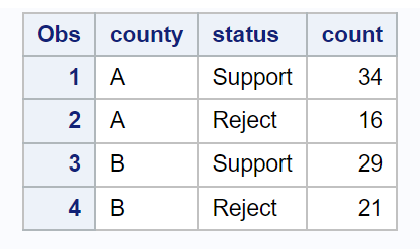
Aşağıdaki kod, her ilçede yasayı destekleyen sakinlerin sayısını özetleyen bir veri kümesinin nasıl oluşturulacağını gösterir:

 /*create dataset*/
data my_data;
    input county $status $count;
    datalines ;
A Bracket 34
A Reject 16
B Bracket 29
B Reject 21
;
run ;

/*view dataset*/
proc print data =my_data;

Daha sonra iki oranlı z testini gerçekleştirmek için PROC FREQ ifadesini Riskdiff (equal var = null) seçeneğiyle birlikte kullanabiliriz:

 /*perform two proportion z-test*/
proc freq data =my_data;
    weightcount ;
    county tables * status / riskdiff ( equal var = null);
run ; 

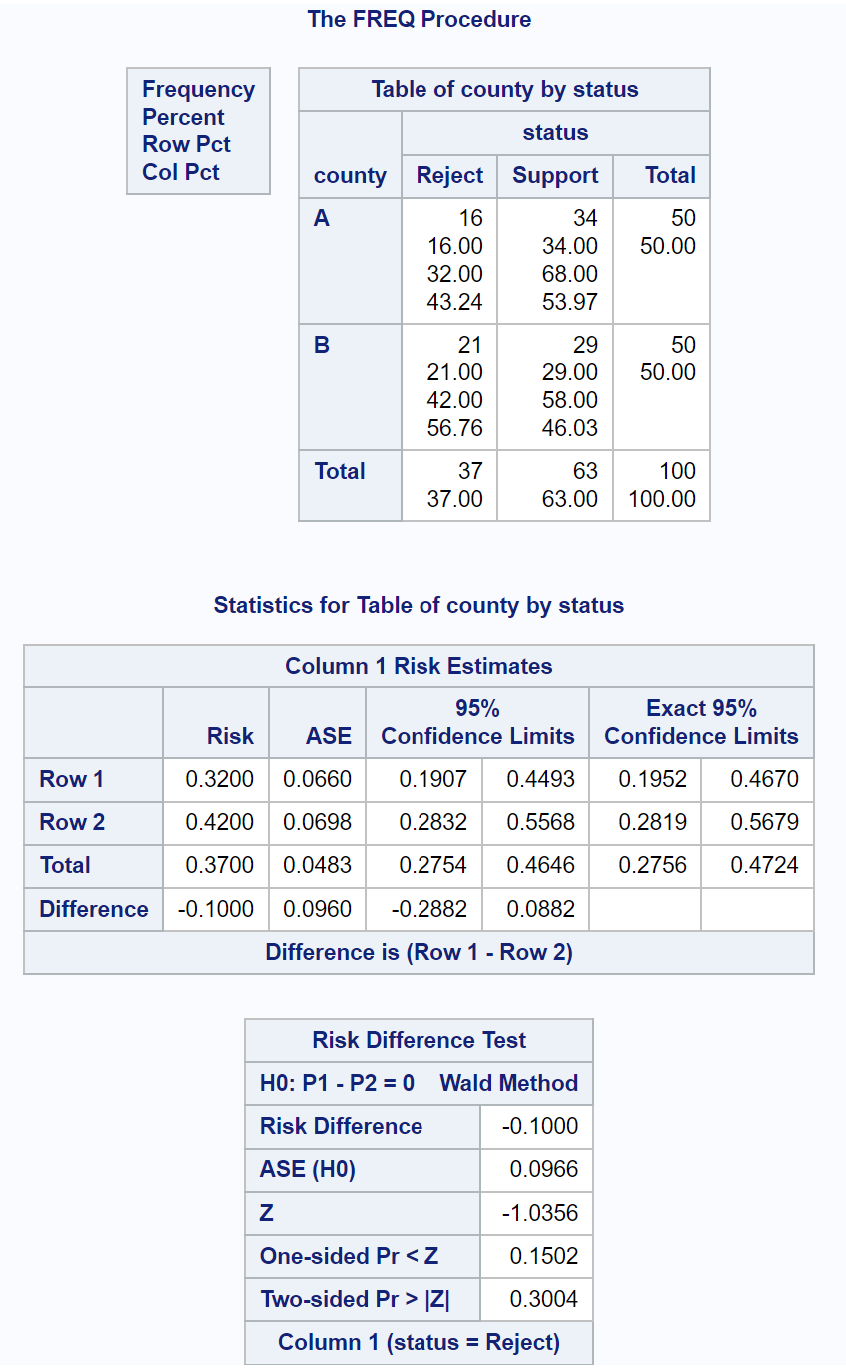
Sonuç tablosundaki Risk Farkı Testi’nden aşağıdaki bilgileri görebiliriz:

• Z testi istatistiği: -1.0356
• İki taraflı p değeri: 0,3004

Bu özel iki oranlı z testi aşağıdaki varsayımları kullandı:

• H ₀ : π ₁ = π ₂ (iki popülasyon oranı eşittir)
• H ₁ : π ₁ ≠ π ₂ (iki popülasyon oranı eşit değildir)

Çıktıdaki p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddedemiyoruz.

Bu, bu yasayı destekleyen sakinlerin oranının iki ilçe arasında farklı olduğunu söyleyecek yeterli kanıtımız olmadığı anlamına geliyor.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer yaygın istatistiksel testlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta tek örnekli t testi nasıl yapılır?
SAS’ta iki örnekli t testi nasıl yapılır?
SAS’ta eşleştirilmiş örnekler t testi nasıl gerçekleştirilir?