Sas'ta lojistik regresyon nasıl gerçekleştirilir?

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullanabileceğimiz bir yöntemdir.

Lojistik regresyon, aşağıdaki formdaki bir denklemi bulmak için maksimum olabilirlik tahmini olarak bilinen bir yöntemi kullanır:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Altın:

• X _j : ^j’inci tahmin değişkeni
• β _j : ^j’inci yordayıcı değişkenin katsayısının tahmini

Denklemin sağ tarafındaki formül, yanıt değişkeninin 1 değerini almasına ilişkin log olasılığını tahmin eder.

Aşağıdaki adım adım örnek, SAS’ta bir lojistik regresyon modelinin nasıl sığdırılacağını gösterir.

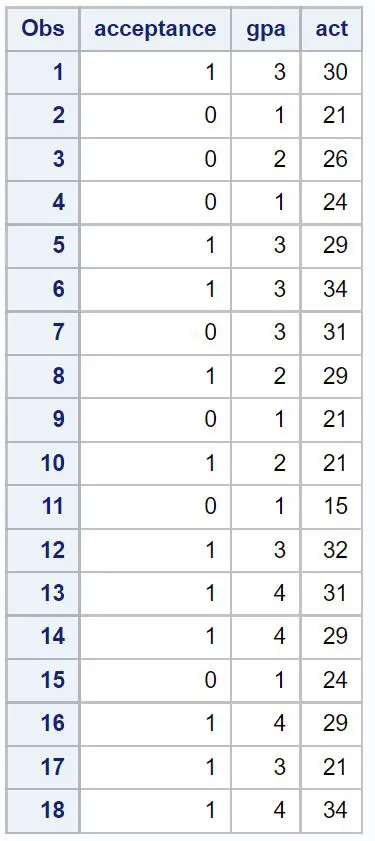
1. Adım: Veri kümesini oluşturun

Öncelikle 18 öğrenci için aşağıdaki üç değişkene ilişkin bilgileri içeren bir veri seti oluşturacağız:

• Belirli bir üniversiteye kabul (1 = evet, 0 = hayır)
• GPA (1’den 4’e kadar ölçek)
• ACT puanı (1’den 36’ya kadar ölçek)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

Adım 2: Lojistik regresyon modelini yerleştirin

Daha sonra, yanıt değişkeni olarak “kabul”ü ve yordayıcı değişkenler olarak “gpa” ve “hareket”i kullanarak lojistik regresyon modeline uyacak şekilde proc lojistiğini kullanacağız.

Not : SAS’ın yanıt değişkeninin 1 değerini alma olasılığını tahmin etmesi için azalmanın belirtilmesi gerekir. SAS, varsayılan olarak yanıt değişkeninin 0 değerini alma olasılığını tahmin eder.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

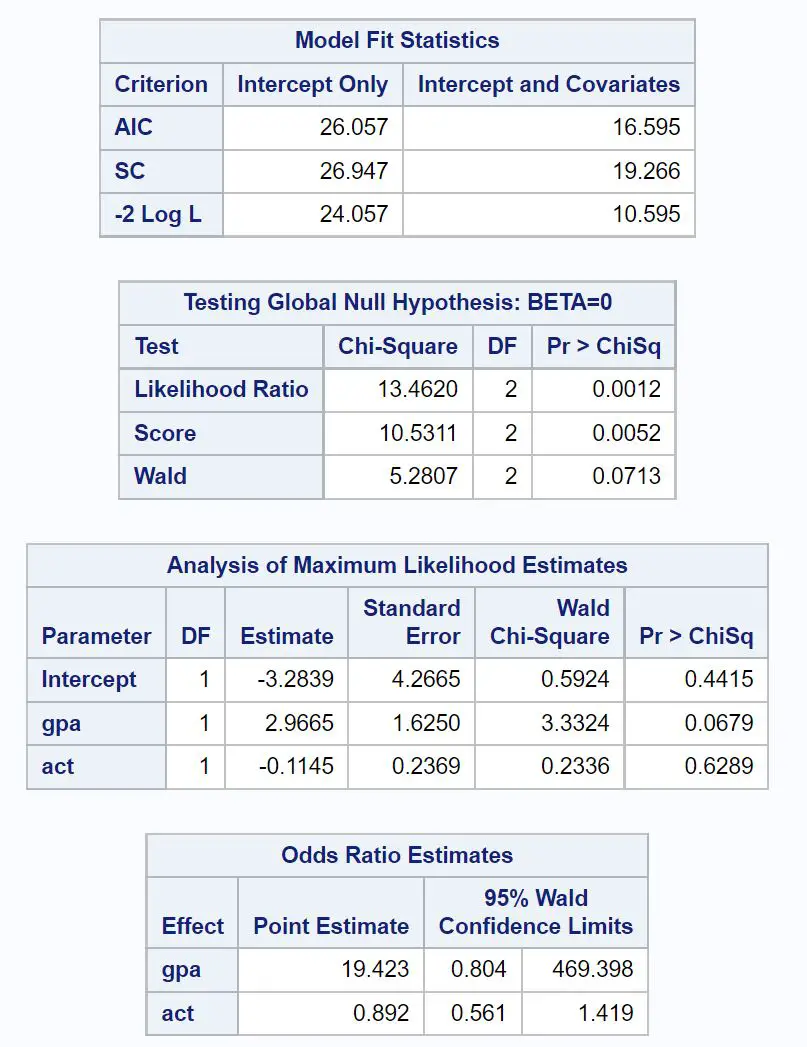
İlk ilgi çekici tablo Model Uyum İstatistikleri başlığını taşıyor.

Bu tablodan modelin 16.595 olarak çıkan AIC değerini görebiliyoruz. AIC değeri ne kadar düşük olursa model verilere o kadar iyi uyum sağlayabilir.

Ancak “iyi” AIC değeri olarak kabul edilen değer için bir eşik yoktur. Bunun yerine, birden fazla modelin uyumunu aynı veri kümesiyle karşılaştırmak için AIC’yi kullanırız. En düşük AIC değerine sahip model genellikle en iyi model olarak kabul edilir.

Bir sonraki ilgi çekici tablo Küresel Sıfır Hipotezinin Test Edilmesi: BETA=0 başlığını taşıyor.

Bu tablodan, 13,4620’lik olabilirlik oranı ki-kare değerini ve buna karşılık gelen 0,0012 p-değerini görebiliriz.

Bu p değeri 0,05’ten küçük olduğundan bu bize lojistik regresyon modelinin bir bütün olarak istatistiksel olarak anlamlı olduğunu söyler.

Daha sonra Maksimum Olabilirlik Tahminlerinin Analizi başlıklı tabloda katsayı tahminlerini analiz edebiliriz.

Bu tablodan, her değişkendeki bir birimlik artış için üniversiteye kabul edilmenin log oranlarındaki ortalama değişimi gösteren gpa ve act katsayılarını görebiliriz.

Örneğin:

• GPA değerindeki bir birimlik artış, üniversiteye kabul edilme log ihtimalinin ortalama 2,9665 artmasıyla ilişkilidir.
• ACT puanındaki bir birimlik artış, üniversiteye kabul edilmenin log ihtimalinde ortalama 0,1145’lik bir düşüşle ilişkilidir.

Sonuçta karşılık gelen p değerleri de bize her bir yordayıcı değişkenin kabul edilme olasılığını tahmin etmede ne kadar etkili olduğuna dair bir fikir verir:

• GPA P değeri: 0,0679
• ACT P değeri: 0,6289

Bu bize GPA’nın üniversiteye kabulün istatistiksel olarak anlamlı bir göstergesi olduğunu, ACT puanının ise istatistiksel olarak anlamlı görünmediğini söylüyor.

Ek kaynaklar

Aşağıdaki eğitimlerde diğer regresyon modellerinin SAS’a nasıl sığdırılacağı açıklanmaktadır:

SAS’ta basit doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta çoklu doğrusal regresyon nasıl gerçekleştirilir?