Fisher'in kesin testi sas'ta nasıl gerçekleştirilir?
Fisher’in kesin testi, iki kategorik değişken arasında anlamlı bir ilişki olup olmadığını belirlemek için kullanılır.
Genellikle 2×2’lik bir tabloda bir veya daha fazla hücre sayısı 5’ten az olduğunda ki-kare bağımsızlık testine alternatif olarak kullanılır.
Fisher kesin testi aşağıdaki boş ve alternatif hipotezleri kullanır:
- H 0 : (sıfır hipotezi) İki değişken bağımsızdır.
- H 1 : (alternatif hipotez) İki değişken bağımsız değildir .
Testin p değeri belirli bir anlamlılık seviyesinden küçükse, testin sıfır hipotezini reddedebilir ve iki değişkenin bağımsız olmadığı, yani anlamlı bir ilişkiye sahip olduğu sonucuna varabiliriz.
Aşağıdaki örnek, Fisher’in kesin testinin SAS’ta nasıl gerçekleştirileceğini gösterir.
Örnek: SAS’ta Fisher’in kesin testi
Belirli bir üniversitede cinsiyetin siyasi parti tercihiyle ilişkili olup olmadığını bilmek istediğimizi varsayalım.
Bunu araştırmak için kampüsteki 25 öğrenciyi rastgele seçiyoruz ve onlara siyasi parti tercihlerini soruyoruz. Sonuçlar aşağıdaki tabloda sunulmaktadır:
| Demokrat | Cumhuriyetçi | |
|---|---|---|
| Dişi | 8 | 4 |
| Erkek | 4 | 9 |
Cinsiyet ile siyasi parti tercihi arasında istatistiksel olarak anlamlı bir ilişki olup olmadığını belirlemek için SAS’ta Fisher’in kesin testini gerçekleştirmek üzere aşağıdaki adımları kullanabiliriz:
1. Adım: Verileri oluşturun
Öncelikle my_data adında bir veri kümesi oluşturalım:
/*create data to hold survey results*/ data my_data; input Party$Gender$; datalines ; Rep Female Rep Female Rep Female Rep Female Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Rep Male Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Female Dem Male Dem Male Dem Male Dem Male ; run ;
Adım 2: Fisher’ın Kesin Testini Gerçekleştirin
Daha sonra Fisher’in kesin testini gerçekleştirmek için aşağıdaki kodu kullanabiliriz:
/*perform Fisher's Exact test*/ proc freq ; Party*Gender / fisher tables ; run ;
Test sonuçları aşağıda gösterilmektedir:
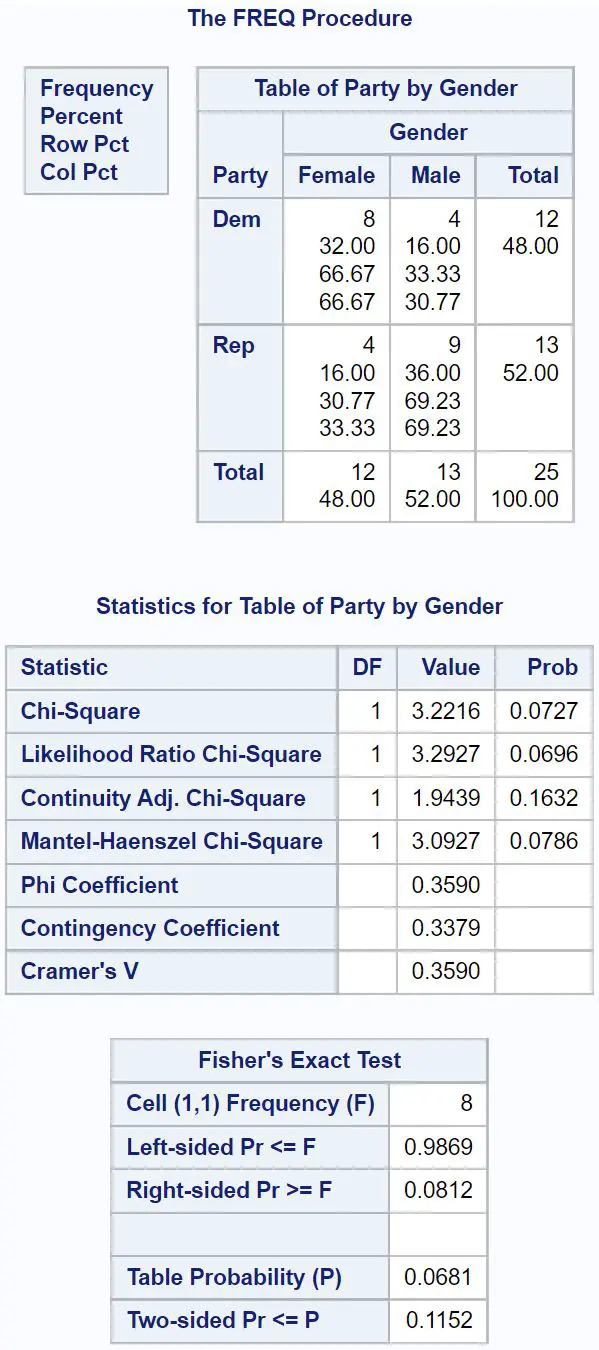
Fisher’in kesin testinin sıfır hipotezi, iki değişkenin bağımsız olduğu yönündedir. Bu örnekte boş hipotezimiz cinsiyet ve siyasi parti tercihlerinin bağımsız olduğu yönündedir ve bu iki kuyruklu bir testtir.
Dolayısıyla, nihai sonuç tablosundaki iki kuyruklu p değerine bakacağız ki bu değer 0,1152 olarak ortaya çıkıyor.
Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddetmiyoruz.
Bu, cinsiyet ile siyasi parti tercihleri arasında anlamlı bir ilişki olduğunu söyleyecek yeterli kanıta sahip olmadığımız anlamına geliyor.
Ek kaynaklar
Aşağıdaki eğitimler Fisher kesin testi hakkında ek bilgi sağlar:
Fisher’in Kesin Testine Giriş
Fisher’ın Kesin Test Hesaplayıcısı
Doğru Fisher Test Sonuçları Nasıl Raporlanır?