Sas'ta pişirme mesafesi nasıl hesaplanır

Cook mesafesi, bir regresyon modelinde etkili gözlemleri tanımlamak için kullanılır.

Cook mesafesinin formülü:

d _ben = (r _i ² / p*MSE) * (h _ii / (1-h _ii ) ² )

Altın:

• r _i ^i’inci kalıntıdır
• p , regresyon modelindeki katsayıların sayısıdır
• MSE ortalama kare hatasıdır
• h _ii ^i’inci kaldıraç değeridir

Cook mesafesi esasen ^i’inci gözlem kaldırıldığında modelin tüm uyum değerlerinin ne kadar değiştiğini ölçer.

Cook mesafesinin değeri ne kadar büyük olursa, belirli bir gözlem o kadar etkili olur.

Genel olarak Cook mesafesi 4/n’den büyük olan herhangi bir gözlemin (burada n = toplam gözlemler) büyük bir etkiye sahip olduğu kabul edilir.

Aşağıdaki örnek, SAS’taki bir regresyon modelinde her gözlem için Cook mesafesinin nasıl hesaplanacağını gösterir.

Örnek: SAS’ta aşçının mesafesini hesaplama

SAS’ta aşağıdaki veri setine sahip olduğumuzu varsayalım:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

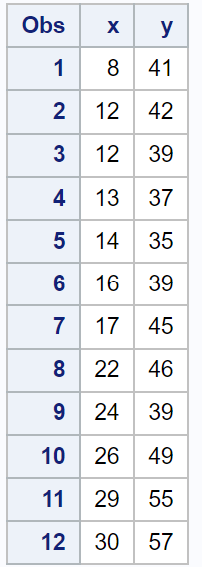
Bu veri setine basit bir doğrusal regresyon modeli uydurmak için PROC REG’i kullanabiliriz, ardından regresyon modelindeki her gözlem için Cook mesafesini hesaplamak amacıyla OUTPUT ifadesini COOKD ifadesi ile birlikte kullanabiliriz:

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

Nihai sonuç tablosu, her gözlem için orijinal veri kümesini Pişirme mesafesiyle birlikte görüntüler:

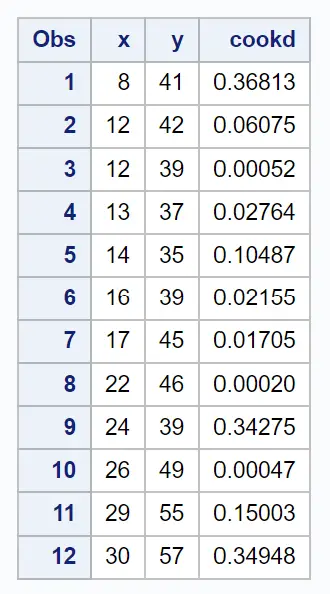
Örneğin şunu görebiliriz:

• İlk gözlem için Cook mesafesi 0,36813’tür .
• İkinci gözlem için Cook mesafesi 0,06075’tir .
• Üçüncü gözlem için Cook mesafesi 0,00052’dir .

Ve benzeri.

PROC REG prosedürü aynı zamanda çıktıda birkaç teşhis grafiği üretir ve Pişirme mesafesi grafiği bu çıktıda görülebilir:

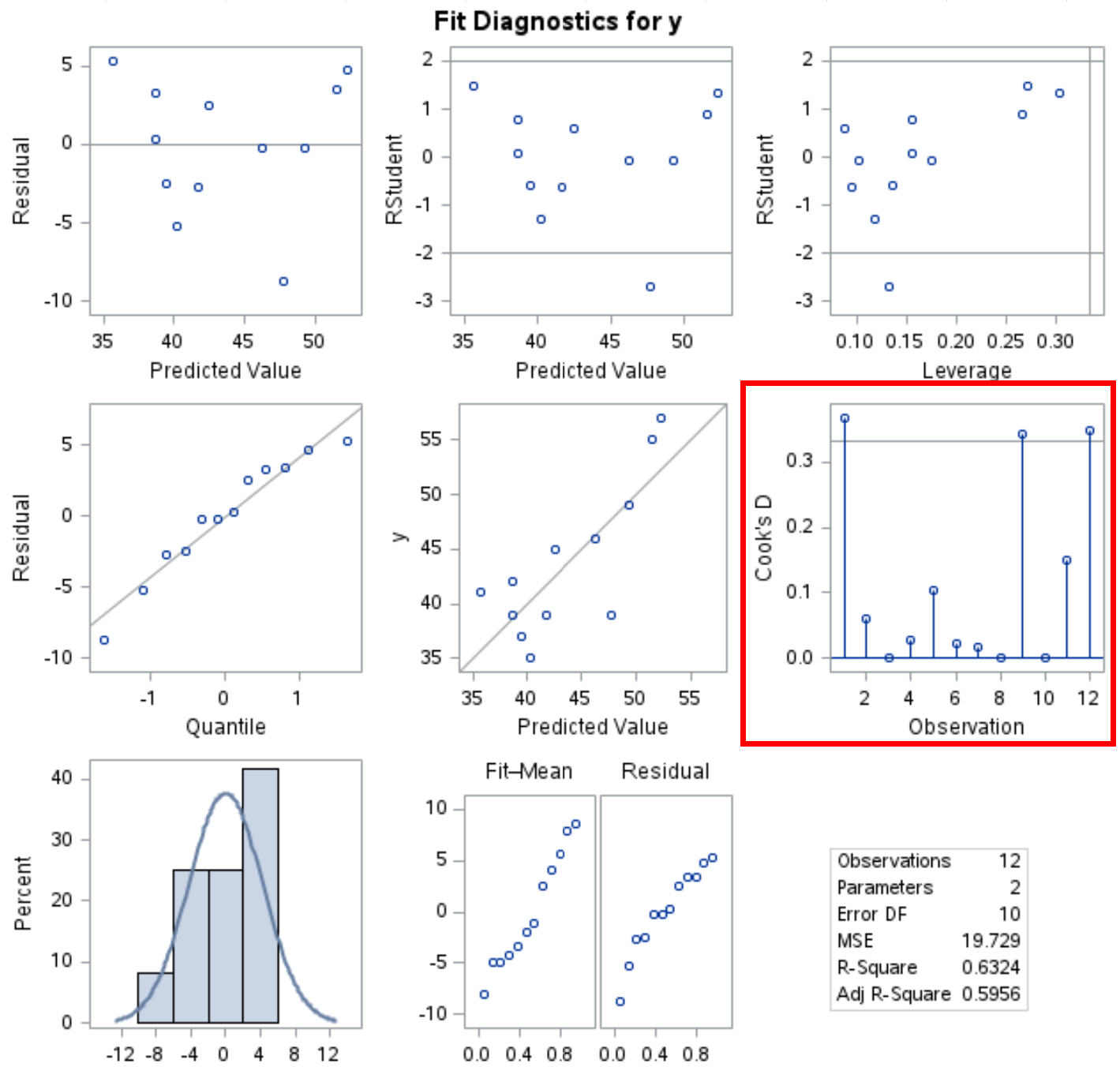
X ekseni gözlem sayısını, y ekseni ise her gözlem için Pişirme mesafesini gösterir.

4/n’ye bir kesme çizgisi yerleştirildiğine dikkat edin (bu durumda n = 12, dolayısıyla kesme 0,33’tür) ve veri kümesindeki üç gözlemin bu çizgiden daha büyük olduğunu görebiliriz.

Bu, bu gözlemlerin regresyon modeli üzerinde büyük bir etkiye sahip olabileceğini ve belki de model sonuçlarını yorumlamadan önce daha yakından incelenmesi gerektiğini göstermektedir.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta Artık Grafik Nasıl Oluşturulur
SAS’ta Histogramlar Nasıl Oluşturulur
SAS’ta nokta bulutları nasıl oluşturulur?
SAS’ta aykırı değerler nasıl belirlenir