Hipergeometrik dağılım

İle Dr.benjamin anderson Ağustos 6, 2023 Olasılık 0 Yorum

Bu yazıda hipergeometrik dağılımın ne olduğunu ve bu tür dağılımla olasılığın nasıl hesaplandığını açıklayacağız. Çevrimiçi olarak hipergeometrik dağılımın formülünü, özelliklerinin neler olduğunu ve ayrıca hipergeometrik dağılımın olasılığını hesaplamak için bir hesap makinesini bulacaksınız.

Hipergeometrik dağılım nedir?

Hipergeometrik dağılım, bir popülasyondan n öğenin değiştirilmesi gerekmeden rastgele bir çıkarma işlemindeki başarılı vakaların sayısını tanımlayan bir olasılık dağılımıdır.

Yani hipergeometrik dağılım, bir popülasyondan herhangi birini değiştirmeden n öğe çıkarırken x başarı elde etme olasılığını hesaplamak için kullanılır.

Hipergeometrik dağılımın üç parametresi vardır:

N : popülasyondaki elementlerin sayısıdır (N = 0, 1, 2,…).
K : Maksimum başarı durumu sayısıdır (K = 0, 1, 2,…,N). Hipergeometrik bir dağılımda bir öğe yalnızca “başarılı” veya “başarısızlık” olarak değerlendirilebileceğinden, NK maksimum başarısızlık durumu sayısıdır.
n : gerçekleştirilen değiştirilmeden getirme sayısıdır.

$X \sim HG(N,K,n)$

Örneğin, N=8, K=5 ve n=3 parametreleriyle hipergeometrik dağılıma sahip ayrık bir rastgele değişken X aşağıdaki şekilde tanımlanır:

$X \sim HG(8,5,3)$

Hipergeometrik dağılım formülü

Hipergeometrik dağılım formülü, K bölü x’in kombinatoryal sayısının, NK bölü nx’in kombinatoryal sayısı ile N bölü n’nin kombinatoryal sayısına bölünmesinin çarpımıdır.

N’nin popülasyon büyüklüğü, K’nın toplam olumlu durum sayısı, n’nin yerine yenisi konulmayan çıkarmaların sayısı ve x’in ise gerçekleşme olasılığının hesaplanması gereken olumlu durumların sayısı olduğu durumlarda.

👉Hipergeometrik dağılıma uyan bir değişkenin olay olasılığını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Hipergeometrik dağılım örneği

Hipergeometrik dağılımın tanımını ve formülünü gördükten sonra, şimdi hipergeometrik dağılımın olasılığını nasıl hesaplayacağınızı bilmeniz için adım adım bir örnek çözeceğiz.

Bir torbaya 20 adet mavi, 30 adet kırmızı top koyuyoruz yani torbanın içerisinde toplam 50 adet top bulunmaktadır. Hiçbirini değiştirmeden 12 top çekersek 4 mavi top çekme olasılığını bulun.

Alıştırmayı çözmek için yapmamız gereken ilk şey hipergeometrik dağılımın parametrelerini belirlemektir. Bu durumda popülasyondaki toplam eleman sayısı 50 ( N =50), maksimum uygun durum sayısı 20 ( K =20) ve 12 top çekiliyor ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

4 mavi top çekme olasılığını hesaplamak istiyoruz ( x =4), bu nedenle hipergeometrik dağılım formülünü uyguluyoruz, değişkenleri karşılık gelen değerlerle değiştiriyoruz ve hesaplamayı gerçekleştiriyoruz:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Hipergeometrik Dağılım Hesaplayıcı

İstenilen olayın meydana gelme olasılığını hesaplamak için hipergeometrik dağılımın parametrelerini aşağıdaki çevrimiçi hesaplayıcıya girin.

N’nin popülasyon büyüklüğü, K’nın toplam olumlu vaka sayısı, n’nin örneklem büyüklüğü ve x’in bunun gerçekleşme olasılığını bulmak istediğimiz değer olduğunu unutmayın.

Hipergeometrik dağılımın özellikleri

Hipergeometrik dağılım aşağıdaki özelliklere sahiptir:

Bir hipergeometrik dağılımın beklenen değeri, örnekteki element sayısı ile olumlu durumların toplam sayısı çarpımının popülasyondaki element sayısına bölünmesine eşittir.

$E[X]=\cfrac{n\cdot K}{N}$

Hipergeometrik dağılımın modu, n+1 çarpı K+1 bölü N+2’nin çarpımından aşağı yuvarlanan değerdir.

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

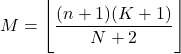
Bir hipergeometrik dağılımın varyansı aşağıdaki ifade kullanılarak elde edilebilir:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

Hipergeometrik bir dağılımın moment üreten fonksiyonu aşağıdaki gibidir:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

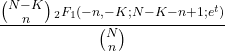
Hipergeometrik dağılımın karakteristik fonksiyonu aşağıdaki gibidir:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

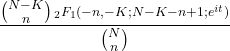
Belirli sayıda olayın meydana gelme olasılığı, hipergeometrik dağılım için özyineleme kullanılarak önceki sayının olasılığından hesaplanabilir:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Hipergeometrik dağılım ve binom dağılımı

Hipergeometrik dağılım ile binom dağılımı arasındaki fark yer değiştirmedir. Hipergeometrik dağılım, alımlar değiştirilmediğinde kullanılır, ancak binom dağılımında alımlar değiştirilir.

Örneğin, bir desteye rastgele beş kart çekiyorsak ve belirli bir kartın çıkma olasılığını hesaplamak istiyorsak, çektiğimiz her kartı değiştirmiyorsak, hesaplamayı yapmak için hipergeometrik dağılımı kullanmamız gerekir. Ancak bir kartı çıkarırken bir sonraki çıkarma işlemini gerçekleştirmeden önce geri koyarsak, olasılığı hesaplamak için binom dağılımını kullanmamız gerekir.

N sayısı büyük, n/N oranı küçük ve istenen olumlu durumların sayısı çok küçük olduğunda, hipergeometrik dağılımı binom dağılımının bir yaklaşımı olarak kullanabiliriz. Ancak sonucun o kadar güvenilir olmayacağı ve üstelik binom yasasıyla olasılıkları hesaplamanın hipergeometri yasasına göre hesaplamaktan daha kolay olması nedeniyle bunu önermiyorum.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil