İki örnekli t testi: tanım, formül ve örnek
İki popülasyonun ortalamalarının eşit olup olmadığını belirlemek için iki örnekli t testi kullanılır.
Bu eğitimde aşağıdakiler açıklanmaktadır:
- İki örnekli bir t testi gerçekleştirme motivasyonu.
- İki örnekli t testi gerçekleştirme formülü.
- İki örnekli t testi gerçekleştirmek için karşılanması gereken varsayımlar.
- İki örnekli t testinin nasıl gerçekleştirileceğine bir örnek.
İki örnekli t testi: Motivasyon
Diyelim ki iki farklı kaplumbağa türünün ortalama ağırlığının eşit olup olmadığını bilmek istiyoruz. Her popülasyonda binlerce kaplumbağa bulunduğundan, her kaplumbağayı ayrı ayrı tartmak çok zaman alıcı ve pahalı olacaktır.
Bunun yerine, her popülasyondan 15 kaplumbağadan oluşanbasit rastgele bir örnek alabilir ve her örneğin ortalama ağırlığını kullanarak, iki popülasyon arasındaki ortalama ağırlığın eşit olup olmadığını belirleyebiliriz:
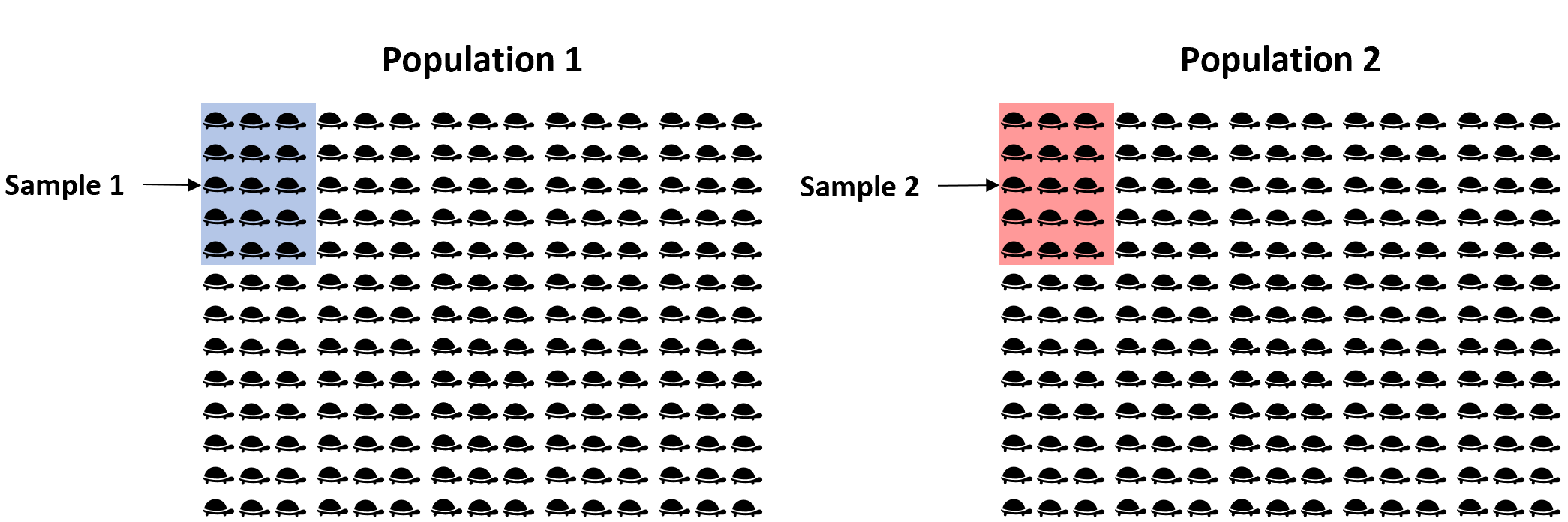
Ancak iki numune arasındaki ortalama ağırlığın en azından biraz farklı olacağı neredeyse garantidir. Soru, bu farkın istatistiksel olarak anlamlı olup olmadığıdır . Neyse ki iki örnekli bir t testi bu soruyu yanıtlamamıza olanak tanıyor.
İki örnekli t testi: formül
İki örnekli bir t testi her zaman aşağıdaki boş hipotezi kullanır:
- H 0 : μ 1 = μ 2 (iki popülasyon ortalaması eşittir)
Alternatif hipotez iki taraflı, sol veya sağ olabilir:
- H 1 (iki kuyruklu): μ 1 ≠ μ 2 (iki popülasyonun ortalamaları eşit değildir)
- H 1 (solda): μ 1 < μ 2 (popülasyon 1’in ortalaması, popülasyon 2’nin ortalamasından düşüktür)
- H 1 (sağ): μ 1 > μ 2 (popülasyon 1’in ortalaması, popülasyon 2’nin ortalamasından daha büyüktür)
T-testi istatistiğini hesaplamak için aşağıdaki formülü kullanırız:
Test istatistiği: ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 )
burada x 1 ve x 2 örnek ortalamalarıdır, n 1 ve n 2 örnek boyutlarıdır ve burada s p aşağıdaki şekilde hesaplanır:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
burada s 1 2 ve s 2 2 örnek varyanslardır.
(n 1 + n 2 -1) serbestlik derecesine sahip t testi istatistiğine karşılık gelen p değeri, seçtiğiniz anlamlılık düzeyinden küçükse (ortak seçenekler 0,10, 0,05 ve 0, 01’dir), o zaman sıfır hipotezini reddedebilir. .
İki örnekli t testi: hipotezler
İki örnekli t testi sonuçlarının geçerli olabilmesi için aşağıdaki varsayımların karşılanması gerekir:
- Bir numunenin gözlemleri diğer numunenin gözlemlerinden bağımsız olmalıdır.
- Veriler yaklaşık olarak normal dağılıma sahip olmalıdır.
- İki numunenin yaklaşık olarak aynı varyansa sahip olması gerekir. Bu varsayım karşılanmazsa bunun yerine Welch t-testini yapmalısınız.
- Her iki örnekten de veriler rastgele örnekleme yöntemi kullanılarak elde edildi.
İki örnekli t testi : örnek
Diyelim ki iki farklı kaplumbağa türünün ortalama ağırlığının eşit olup olmadığını bilmek istiyoruz. Bunu test etmek için aşağıdaki adımları kullanarak α = 0,05 anlamlılık düzeyinde iki örnekli bir t testi gerçekleştireceğiz:
Adım 1: Örnek verileri toplayın.
Her popülasyondan aşağıdaki bilgilerle birlikte rastgele bir kaplumbağa örneği topladığımızı varsayalım:
Örnek 1:
- Örneklem büyüklüğü n 1 = 40
- Ortalama numune ağırlığı x 1 = 300
- Örneklem standart sapması s 1 = 18,5
Örnek 2:
- Örneklem büyüklüğü n 2 = 38
- Ortalama numune ağırlığı x 2 = 305
- Örneklem standart sapması s 2 = 16,7
Adım 2: Varsayımları tanımlayın.
İki örnekli t testini aşağıdaki varsayımlarla gerçekleştireceğiz:
- H 0 : μ 1 = μ 2 (iki popülasyon ortalaması eşittir)
- H 1 : μ 1 ≠ μ 2 (iki popülasyon ortalaması eşit değildir)
Adım 3: t -testi istatistiğini hesaplayın.
İlk olarak, birleştirilmiş standart sapma s p’yi hesaplayacağız:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2) = √ ( 40-1)18,5 2 + (38-1) 16,7 2 / (40+38-2) = 17,647
Daha sonra t -test istatistiğini hesaplayacağız:
t = ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 ) = (300-305) / 17,647(√ 1/40 + 1/38 ) = -1,2508
Adım 4: t- testi istatistiğinin p-değerini hesaplayın.
T Puanı – P Değeri Hesaplayıcısına göre, t = -1,2508 ve serbestlik derecesi = n 1 + n 2 -2 = 40+38-2 = 76 ile ilişkili p değeri 0,21484’tür .
Adım 5: Bir sonuç çıkarın.
Bu p değeri bizim anlamlılık düzeyimiz olan α = 0,05’ten düşük olmadığı için sıfır hipotezini reddedemiyoruz. Bu iki popülasyon arasındaki kaplumbağaların ortalama ağırlığının farklı olduğunu söyleyecek yeterli kanıtımız yok.
Not: Bu iki örnekli t testinin tamamını , iki örnekli t testi hesaplayıcısını kullanarak da gerçekleştirebilirsiniz.
Ek kaynaklar
Aşağıdaki eğitimlerde farklı istatistiksel programlar kullanılarak iki örnekli t testinin nasıl gerçekleştirileceği açıklanmaktadır:
Excel’de iki örnekli t testi nasıl yapılır
SPSS’de iki örnekli t testi nasıl yapılır
Stata’da iki örnekli t testi nasıl yapılır?
R’de iki örnekli t testi nasıl yapılır
Python’da iki örnekli t testi nasıl yapılır
TI-84 Hesap Makinesinde İki Örnekli t-Testi Nasıl Gerçekleştirilir
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil