Excel: i̇ki veri kümesinin i̇statistiksel karşılaştırmasını oluşturun

Çoğu zaman, her bir veri kümesindeki değerlerin dağılımının nasıl farklılaştığını anlamak için Excel’de iki veri kümesinin istatistiksel karşılaştırmasını yapmak isteyebilirsiniz.

İstatistiksel karşılaştırma yapmanın iki yaygın yolu vardır:

Yöntem 1: Her veri kümesinin beş basamaklı özetini hesaplayın

Her veri setinin aşağıdaki değerlerden oluşan beş rakamlı özetini hesaplayabiliriz:

• Asgari değer
• İlk çeyrek (25. yüzdelik dilim)
• Medyan (50. yüzdelik dilim)
• Üçüncü çeyrek (75. yüzdelik dilim)
• Maksimum

Bu beş değeri hesaplayarak her bir veri setindeki değerlerin dağılımını iyi bir şekilde anlayabiliriz.

Yöntem 2: Ortalamayı ve standart sapmayı hesaplayın

İki veri kümesinin istatistiksel karşılaştırmasını yapmanın daha basit bir yolu, her veri kümesinin ortalamasını ve standart sapmasını hesaplamaktır.

Bu, yaklaşık olarak “merkezi” değerin nerede olduğunu ve her veri setinde değerlerin dağılımının nasıl olduğunu anlamamıza yardımcı olur.

Aşağıdaki örnek, bu yöntemlerin her birinin pratikte nasıl kullanılacağını göstermektedir.

Örnek: Excel’de iki veri kümesinin istatistiksel karşılaştırmasını gerçekleştirin

Excel’de, iki farklı sınıftaki öğrencilerin belirli bir sınavda elde ettiği sonuçları gösteren iki veri setimiz olduğunu varsayalım:

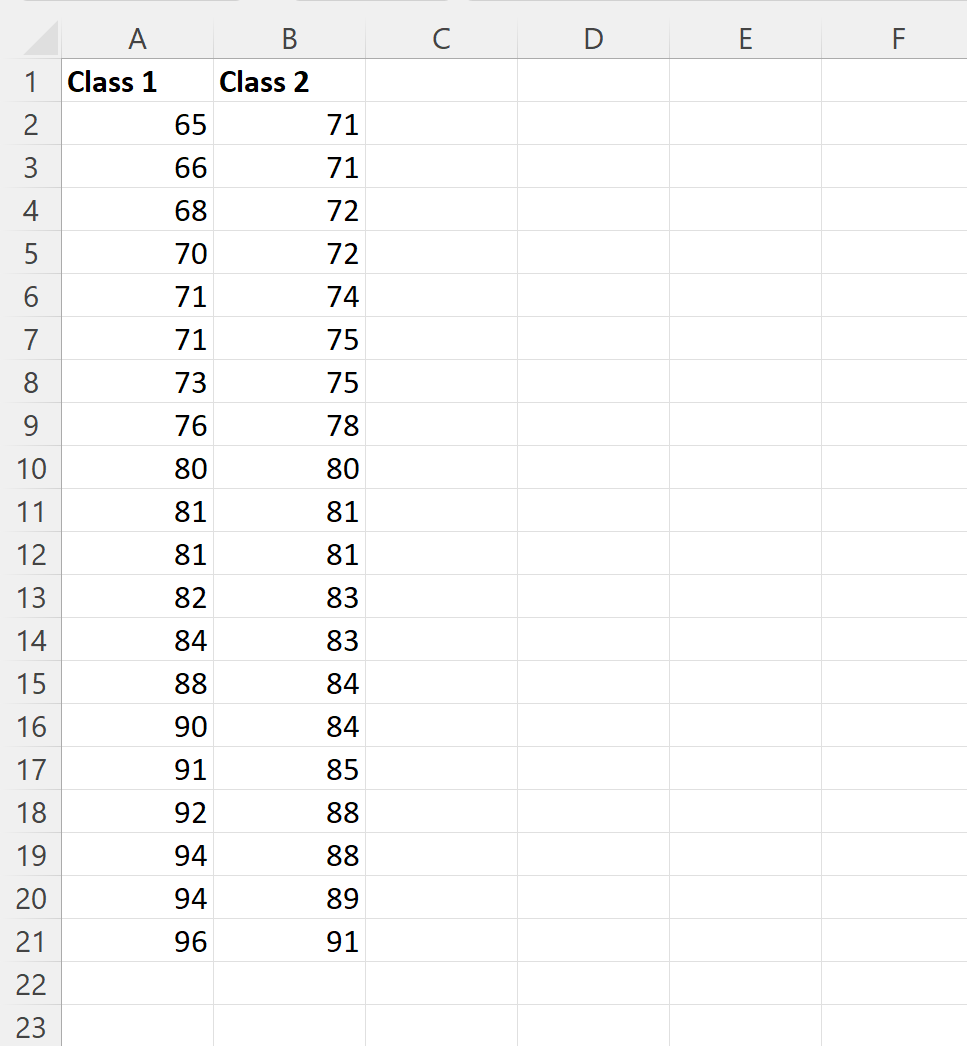
1.sınıf sınav sonuçlarının beş haneli özetini hesaplamak için E sütunundaki hücrelere aşağıdaki formülleri yazabiliriz:

• E2 : =MIN(A2:A21)
• E3 : =DÖRTTEBİR(A2:A21; 1)
• E4 : =MEDYAN(A2:A21)
• E5 : =DÖRTTEBİR(A2:A21, 3)
• E6 : =MAKS(A2:A21

Daha sonra sınıf 2 için aynı değerleri hesaplamak için bu formüllere tıklayıp sağa sürükleyebiliriz:

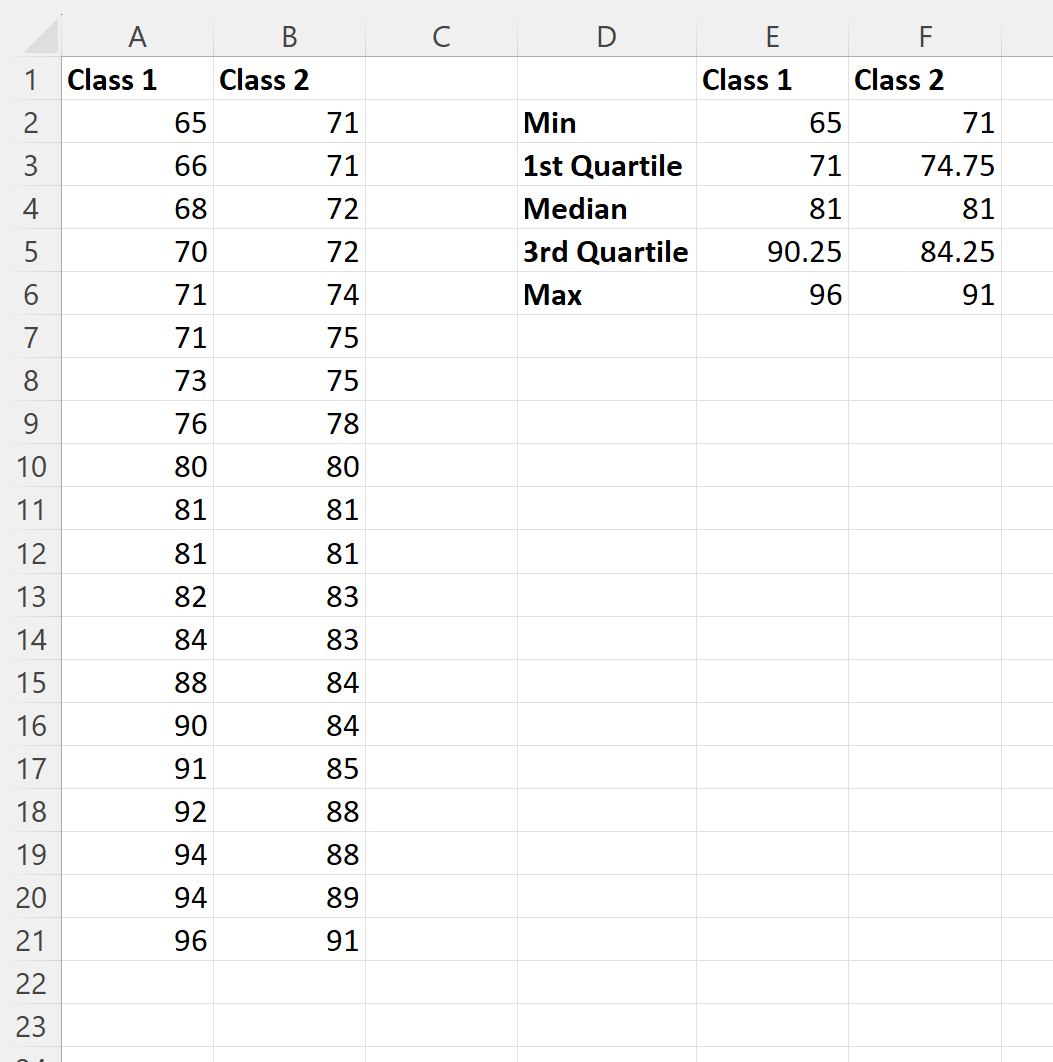
Daha sonra Sınıf 1 sınav sonuçlarının ortalamasını ve standart sapmasını hesaplamak için E sütunundaki hücrelere aşağıdaki formülleri girebiliriz:

• E8 : =ORTALAMA(A2:A21)
• E9 : =ETDEV(A2:A21; 1)

Daha sonra sınıf 2 için aynı değerleri hesaplamak için bu formüllere tıklayıp sağa sürükleyebiliriz:

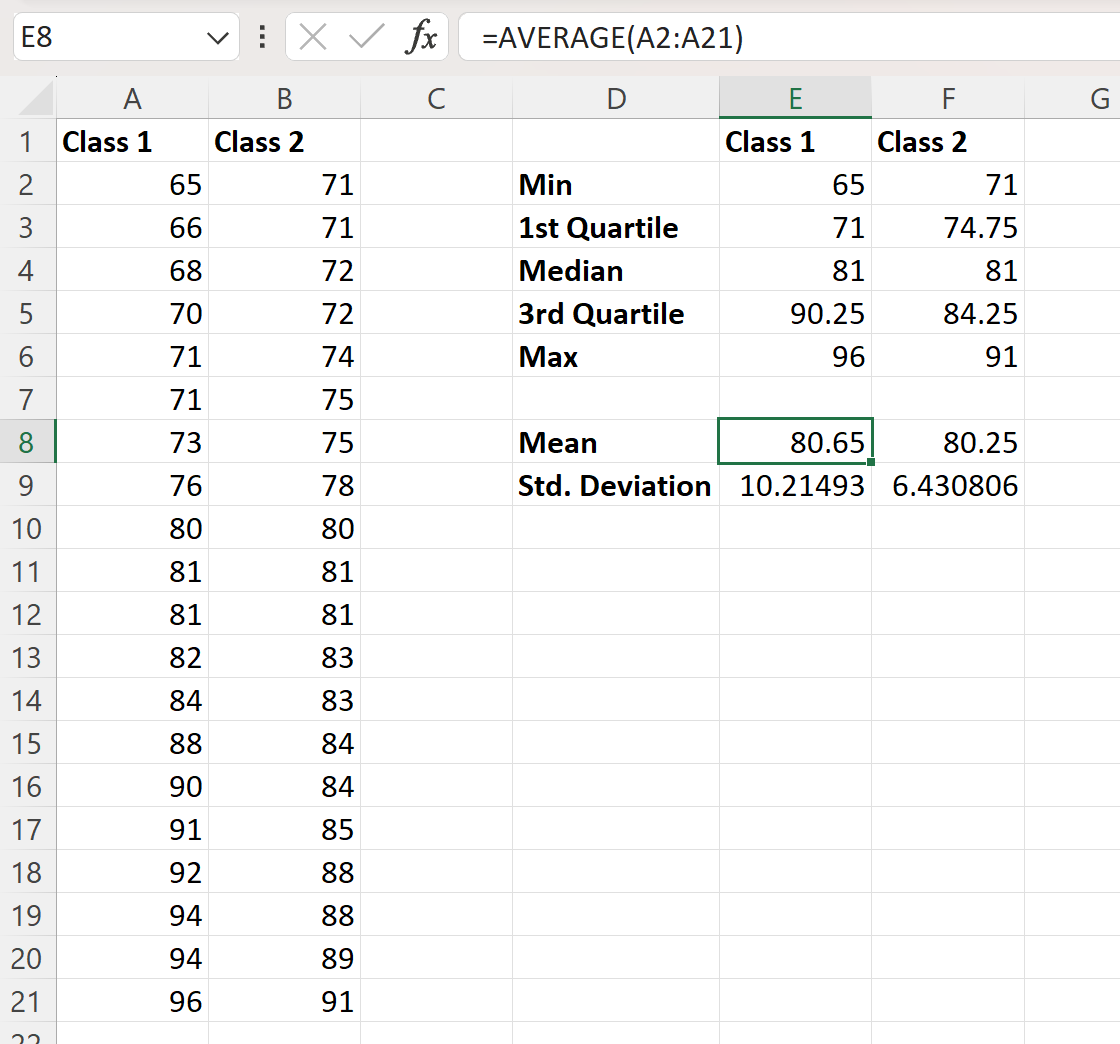
İki veri setinin bu istatistiksel karşılaştırmasından aşağıdaki sonuçları çıkarabiliriz:

Sonuç 1: Her iki veri kümesi de benzer “temel” değere sahiptir.

Her iki veri kümesinin de ortalama sınav puanı 81’dir. Ortalama değerler yalnızca biraz farklıdır: birinci sınıfın ortalama sınav puanı 80,65, ikinci sınıfın ortalama sınav puanı 80,65, ikinci sınıfın ortalama sınav puanı ise 80,65’tir. 80.65′ 80.25’in incelemesi.

Bu bize iki sınıf arasındaki “temel” veya “tipik” sınav puanının benzer olduğunu söylüyor.

Sonuç 2: İlk veri seti çok daha büyük bir değer “dağılımına” sahiptir.

Çeşitli göstergeler bize birinci sınıf sınavlarının sonuçlarının ikinci sınıfa göre çok daha dağınık olduğunu söylüyor.

Örneğin, sınıf 1’in kapsamı çok daha yüksektir:

• Sınıf 1 aralığı: 96 – 65 = 31
• Sınıf 2 aralığı: 91 – 71 = 20

Sınıf 1’in çeyrekler arası aralığı da çok daha yüksektir:

• Sınıf 1 çeyrekler arası aralık: 90,25 – 71 = 19,25
• Sınıf 2 çeyrekler arası aralık: 84,25 – 74,75 = 9,5

Sınıf 1’in standart sapması da çok daha yüksektir:

• Sınıf 1 standart sapması: 10,21
• Sınıf 2’nin standart sapması: 6,43

Bu önlemlerin her biri bize 1. Sınıf öğrencilerinin sınav puanlarındaki farkın 2. Sınıf öğrencilerine göre çok daha yüksek olduğunu söylüyor.

Ek kaynaklar

Aşağıdaki eğitimlerde Excel’de diğer yaygın işlemlerin nasıl gerçekleştirileceği açıklanmaktadır:

Excel’de Özet Tablo Nasıl Oluşturulur
Medyan Excel’de gruba göre nasıl hesaplanır
Excel’de Standart Sapma Nasıl Hesaplanır ve Sıfır Nasıl Yoksayılır