İki yönlü anova: tanım, formül ve örnek

İki değişkene (bazen “faktörler” olarak da adlandırılır) atanan üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için iki yönlü bir ANOVA (“varyans analizi”) kullanılır.

Bu eğitimde aşağıdakiler açıklanmaktadır:

• İki yönlü ANOVA ne zaman kullanılır?
• İki yönlü ANOVA gerçekleştirmek için karşılanması gereken varsayımlar.
• İki yönlü ANOVA’nın nasıl gerçekleştirileceğine bir örnek.

İki yönlü ANOVA ne zaman kullanılır?

İki faktörün bir yanıt değişkenini nasıl etkilediğini ve iki faktör arasında yanıt değişkeni üzerinde bir etkileşim etkisinin olup olmadığını bilmek istediğinizde iki yönlü ANOVA kullanmalısınız.

Örneğin, bir botanikçinin güneşe maruz kalmanın ve sulama sıklığının bitki büyümesini nasıl etkilediğini araştırmak istediğini varsayalım. 40 tohum ekiyor ve iki ay boyunca farklı güneş ışığı koşullarında ve sulama sıklığında büyümelerini sağlıyor. İki ay sonra her bitkinin yüksekliğini kaydediyor.

Bu durumda aşağıdaki değişkenlere sahibiz:

• Tepki değişkeni: bitki büyümesi
• Faktörler: güneşe maruz kalma, sulama sıklığı

Ve şu sorulara yanıt vermek istiyoruz:

• Güneşe maruz kalmak bitki büyümesini etkiler mi?
• Sulama sıklığı bitki büyümesini etkiler mi?
• Güneşe maruz kalma ile sulama sıklığı arasında bir etkileşim etkisi var mı? (örneğin güneşe maruz kalmanın bitkiler üzerindeki etkisi sulama sıklığına bağlıdır)

Bu analiz için iki yönlü ANOVA kullanacağız çünkü iki faktörümüz var. Bunun yerine, yalnızca sulama sıklığının bitki büyümesini ne kadar etkilediğini bilmek isteseydik, yalnızca tek faktörle çalışacağımız için tek yönlü ANOVA kullanırdık.

İki yönlü ANOVA’nın varsayımları

İki yönlü ANOVA sonuçlarının geçerli olabilmesi için aşağıdaki varsayımların karşılanması gerekir:

1. Normallik – Yanıt değişkeni her grup için yaklaşık olarak normal şekilde dağıtılır.

2. Eşit Varyasyonlar – Her grup için varyanslar yaklaşık olarak eşit olmalıdır.

3. Bağımsızlık – Her grup içindeki gözlemler birbirinden bağımsızdır ve gruplar içindeki gözlemler rastgele örnekleme yoluyla elde edilmiştir.

İki yönlü ANOVA: örnek

Bir botanikçi bitki büyümesinin güneş ışığına maruz kalma ve sulama sıklığından etkilenip etkilenmediğini bilmek ister. 40 tohum ekiyor ve iki ay boyunca farklı güneş ışığı koşullarında ve sulama sıklığında büyümelerini sağlıyor. İki ay sonra her bitkinin yüksekliğini kaydediyor. Sonuçlar aşağıda gösterilmektedir:

Yukarıdaki tabloda her bir koşul kombinasyonunda beş bitkinin yetiştirildiğini görüyoruz.

Örneğin, beş bitki günlük sulamayla ve güneş ışığı olmadan büyütüldü ve iki ay sonra boyları 4,8 inç, 4,4 inç, 3,2 inç, 3,9 inç ve 4,4 inç oldu:

Excel’de iki yönlü bir ANOVA gerçekleştirir ve aşağıdaki sonucu elde eder:

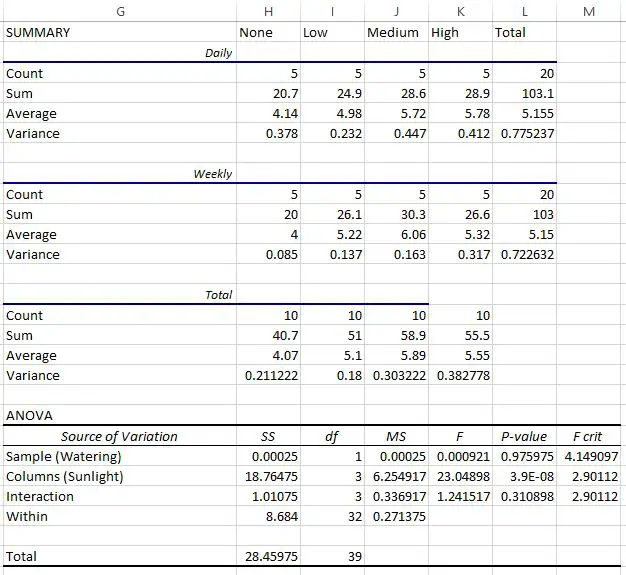
Son tablo iki yönlü ANOVA’nın sonucunu göstermektedir. Şunları gözlemleyebiliriz:

• Sulama sıklığı ile güneşe maruz kalma arasındaki etkileşimin p değeri 0,310898 idi. Bu durum 0,05 alfa düzeyinde istatistiksel olarak anlamlı değildir.
• Sulama sıklığına ilişkin p değeri 0,975975’tir . Bu durum 0,05 alfa düzeyinde istatistiksel olarak anlamlı değildir.
• Güneşe maruz kalmanın p değeri 3,9E-8 (0,000000039) idi. Bu, 0,05 alfa seviyesinde istatistiksel olarak anlamlıdır.

Bu sonuçlar, bitki boyu üzerinde istatistiksel olarak anlamlı etkiye sahip tek faktörün güneşe maruz kalma olduğunu göstermektedir.

Etkileşim etkisi olmadığından güneşe maruz kalmanın etkisi, sulama sıklığının her seviyesinde tutarlıdır.

Basitçe söylemek gerekirse, bir bitkinin günlük veya haftalık olarak sulanmasının, güneşe maruz kalmanın bitkiyi nasıl etkilediği üzerinde hiçbir etkisi yoktur.

Ek kaynaklar

Aşağıdaki makaleler, farklı istatistiksel yazılımlar kullanılarak iki yönlü ANOVA’nın nasıl gerçekleştirileceğini açıklamaktadır:

Excel’de İki Yönlü ANOVA Nasıl Gerçekleştirilir
R’de iki yönlü ANOVA nasıl gerçekleştirilir
Python’da İki Yönlü ANOVA Nasıl Gerçekleştirilir
SPSS’de İki Yönlü ANOVA Nasıl Gerçekleştirilir
Stata’da iki yönlü ANOVA nasıl gerçekleştirilir?