Python'da ikinci dereceden regresyon nasıl gerçekleştirilir?

İkinci dereceden regresyon, gerçek ilişkiler ikinci dereceden olduğunda, bir grafikte “U” veya ters çevrilmiş “U” gibi görünebilen, bir tahmin değişkeni ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanabileceğimiz bir regresyon türüdür.

Yani yordayıcı değişken arttıkça tepki değişkeni de artma eğiliminde olur ancak belli bir noktadan sonra yordayıcı değişken artmaya devam ettikçe yanıt değişkeni azalmaya başlar.

Bu eğitimde Python’da ikinci dereceden regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Python’da İkinci Dereceden Regresyon

16 farklı kişi için haftada çalışılan saat sayısına ve rapor edilen mutluluk düzeyine (0’dan 100’e kadar bir ölçekte) ilişkin verilerimiz olduğunu varsayalım:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

Bu verinin basit bir dağılım grafiğini yaparsak iki değişken arasındaki ilişkinin “U” şeklinde olduğunu görebiliriz:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

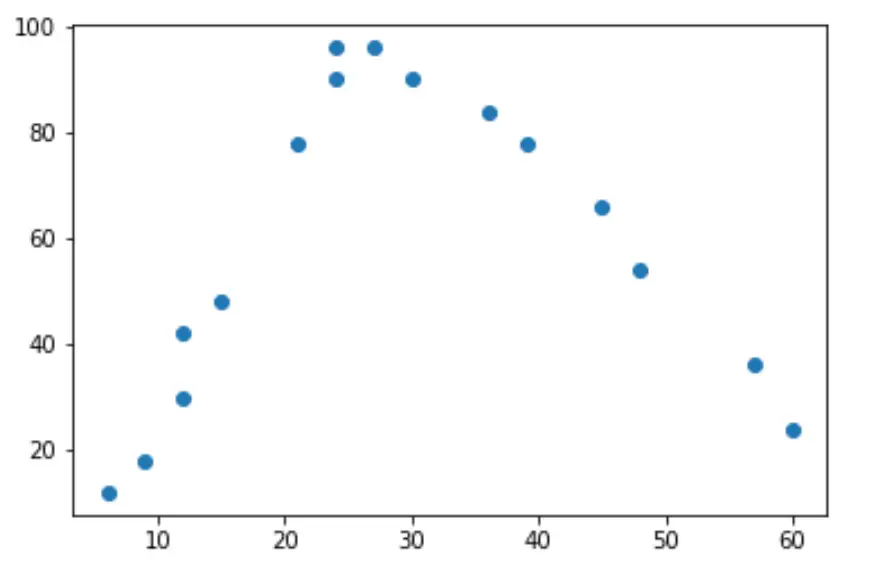
Çalışma saatleri arttıkça mutluluk da artıyor ancak çalışma saatleri haftada yaklaşık 35 saati aştığında mutluluk azalmaya başlıyor.

Bu “U” şekli nedeniyle bu, ikinci dereceden regresyonun iki değişken arasındaki ilişkiyi ölçmek için muhtemelen iyi bir aday olduğu anlamına gelir.

Gerçekten ikinci dereceden bir regresyon gerçekleştirmek için numpy.polyfit() işlevini kullanarak derecesi 2 olan bir polinom regresyon modeli yerleştirebiliriz :

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

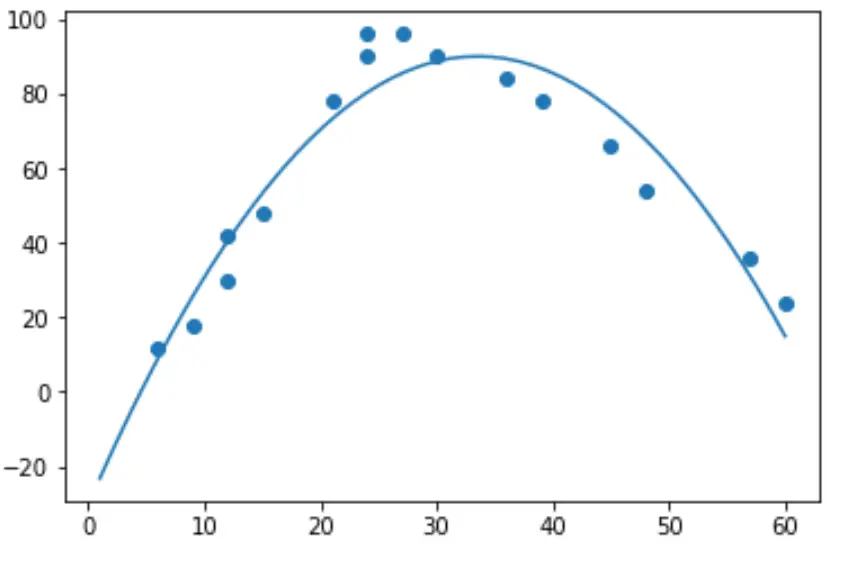
Uygun polinom regresyon denklemini model katsayılarını yazdırarak elde edebiliriz:

 print (model)

-0.107x 2 + 7.173x - 30.25

Uygun ikinci dereceden regresyon denklemi:

Mutluluk = -0,107(saat) ² + 7,173(saat) – 30,25

Bu denklemi, bireyin çalışma saatlerine göre beklenen mutluluk düzeyini hesaplamak için kullanabiliriz. Örneğin haftada 30 saat çalışan bir kişinin beklenen mutluluk düzeyi:

Mutluluk = -0,107(30) ² + 7,173(30) – 30,25 = 88,64 .

Ayrıca, yordayıcı değişkenler tarafından açıklanabilen yanıt değişkenindeki varyansın oranı olan modelin R-karesini elde etmek için kısa bir fonksiyon da yazabiliriz.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

Bu örnekte modelin R karesi 0,9092’dir .

Bu, bildirilen mutluluk düzeylerindeki değişimin %90,92’sinin yordayıcı değişkenler tarafından açıklanabileceği anlamına gelir.

Ek kaynaklar

Python’da polinom regresyonu nasıl gerçekleştirilir
R’de ikinci dereceden regresyon nasıl gerçekleştirilir?
Excel’de ikinci dereceden regresyon nasıl gerçekleştirilir