R'de ikinci dereceden regresyon nasıl gerçekleştirilir?

İki değişkenin doğrusal bir ilişkisi olduğunda, ilişkilerini ölçmek için sıklıkla basit doğrusal regresyon kullanabiliriz.

Bununla birlikte, iki değişken ikinci dereceden bir ilişkiye sahip olduğunda, ilişkilerini ölçmek için ikinci dereceden regresyonu kullanabiliriz.

Bu eğitimde R’de ikinci dereceden regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: R’de ikinci dereceden regresyon

Çalışılan saat sayısı ile bildirilen mutluluk arasındaki ilişkiyi anlamak istediğimizi varsayalım. 11 farklı kişi için haftada çalışılan saat sayısı ve rapor edilen mutluluk düzeyi (0’dan 100’e kadar bir ölçekte) hakkında aşağıdaki verilere sahibiz:

R’ye ikinci dereceden bir regresyon modelini sığdırmak için aşağıdaki adımları kullanın.

Adım 1: Verileri girin.

İlk olarak verilerimizi içeren bir veri çerçevesi oluşturacağız:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Adım 2: Verileri görselleştirin.

Daha sonra verileri görselleştirmek için basit bir dağılım grafiği oluşturacağız.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

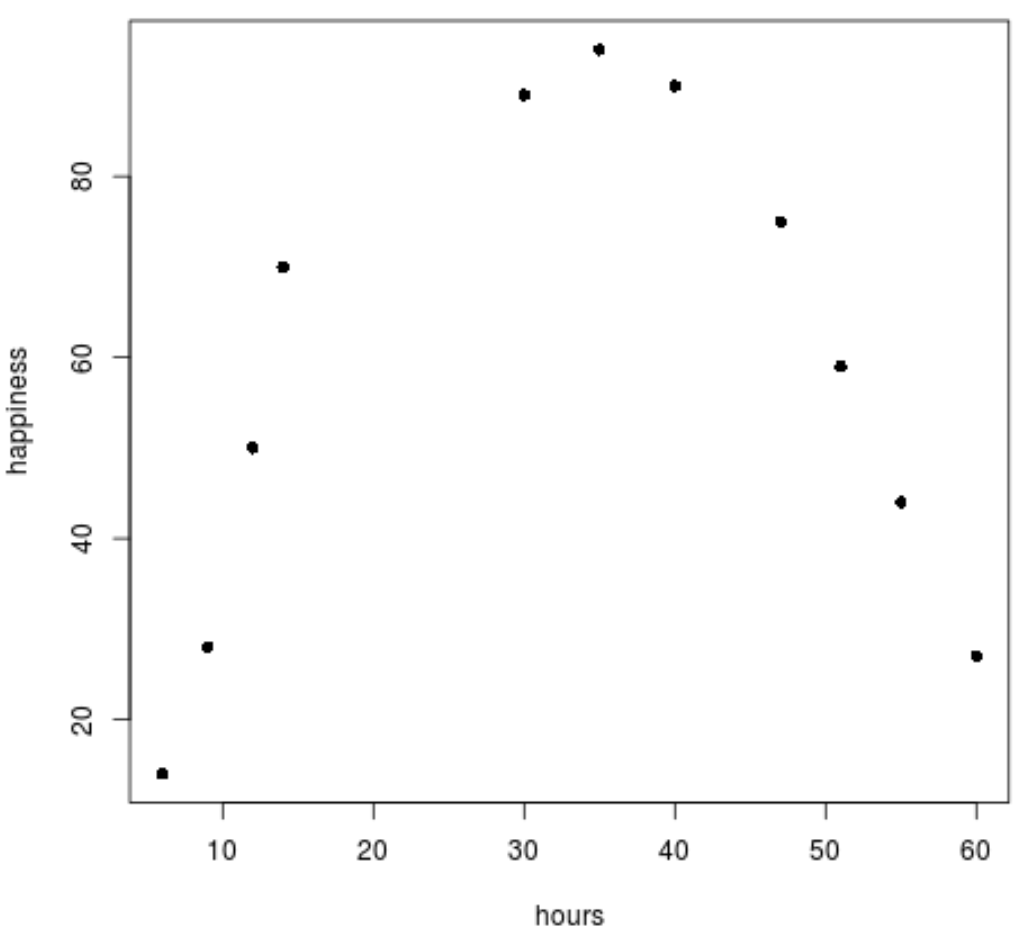
Verilerin doğrusal bir kalıp izlemediğini açıkça görebiliyoruz.

Adım 3: Basit bir doğrusal regresyon modeli yerleştirin.

Daha sonra verilere ne kadar iyi uyduğunu görmek için basit bir doğrusal regresyon modeli uygulayacağız:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

Model tarafından açıklanan mutluluktaki toplam varyans, çoklu R-kare değerinin gösterdiği gibi yalnızca %4,46’dır .

Adım 4: İkinci dereceden bir regresyon modeli yerleştirin.

Daha sonra ikinci dereceden bir regresyon modeli uygulayacağız.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

Modelin açıkladığı mutluluktaki toplam varyans %96,02’ye yükseldi.

Modelin verilere ne kadar iyi uyduğunu görselleştirmek için aşağıdaki kodu kullanabiliriz:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

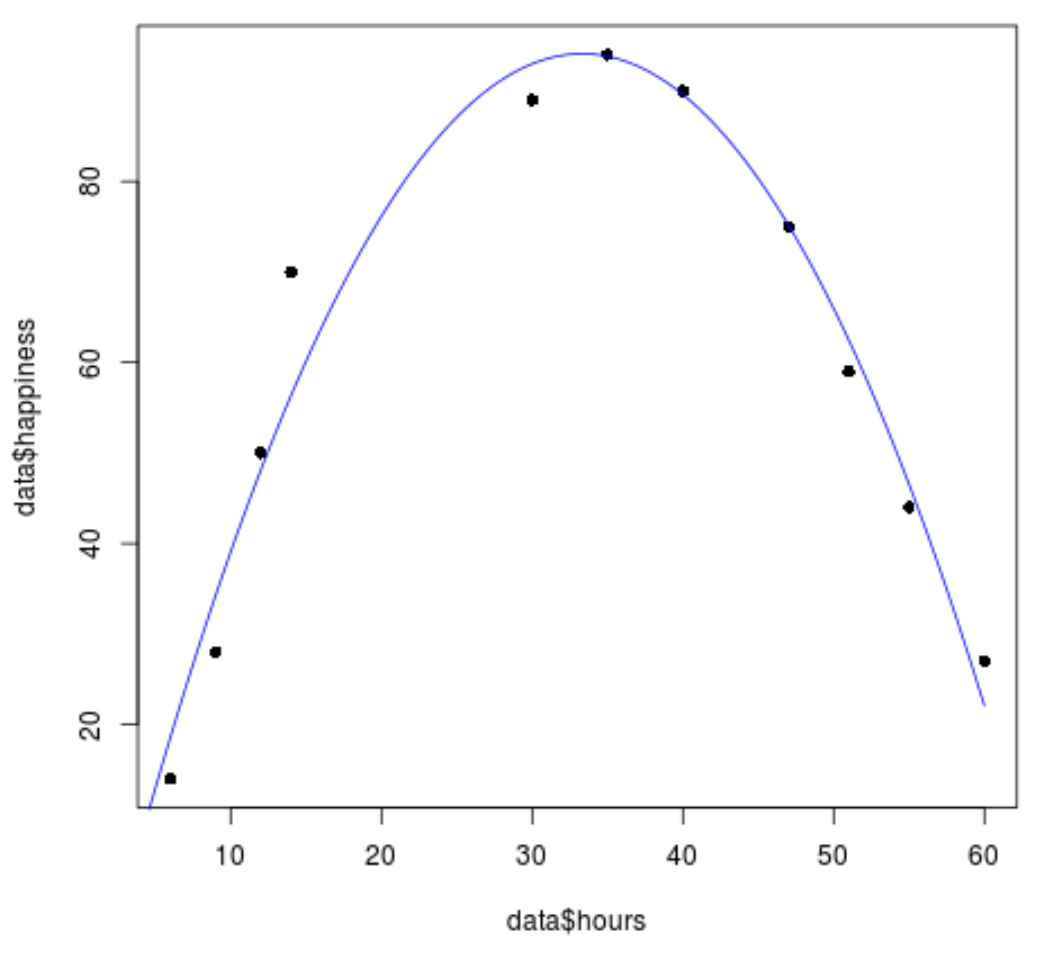
İkinci dereceden regresyon çizgisinin veri değerlerine oldukça iyi uyum sağladığını görebiliriz.

Adım 5: İkinci dereceden regresyon modelini yorumlayın.

Bir önceki adımda ikinci dereceden regresyon modelinin sonucunun şöyle olduğunu gördük:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

Burada sunulan katsayılara dayanarak düzeltilmiş ikinci dereceden regresyon şu şekilde olacaktır:

Mutluluk = -0,1012 (saat) ² + 6,7444 (saat) – 18,2536

Bu denklemi, bir bireyin haftada kaç saat çalıştığı göz önüne alındığında tahmin edilen mutluluğunu bulmak için kullanabiliriz.

Örneğin haftada 60 saat çalışan bir kişinin mutluluk düzeyi 22,09 olacaktır:

Mutluluk = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Haftada 30 saat çalışan bir kişinin ise mutluluk düzeyi 92,99 olmalıdır:

Mutluluk = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99