Socs: dağılımları tanımlamak için kullanışlı bir kısaltma

İstatistikte genellikle bir veri kümesinin nasıl dağıtıldığını anlamak isteriz. Özellikle bir dağıtım hakkında bilinmesi yararlı olan dört şey vardır:

1 . Şekil

• Dağılım simetrik mi yoksa bir tarafa çarpık mı?
• Dağılım tek modlu mu (tek tepe) yoksa çift modlu mu (iki tepe)?

2. Aykırı Değerler

• Dağılımda aykırı değerler var mı?

3. Merkez

• Ortalama, medyan ve dağılım şekli nedir?

4.Yayılma

• Dağılımın aralığı, çeyrekler arası aralığı, standart sapması ve varyansı nedir?

SOCS bu dört şeyi hatırlamak için kullanabileceğimiz kullanışlı bir kısaltmadır. “Şekil, aykırı değerler, merkez, yayılma” anlamına gelir.

Bir dağıtımı tanımlamak için SOCS’nin nasıl kullanılacağına dair basit bir örnek üzerinden gidelim.

Örnek: Bir dağıtımı tanımlamak için SOCS nasıl kullanılır?

Diyelim ki 20 farklı bitki örneğinin boyunu gösteren aşağıdaki veri setine sahibiz.

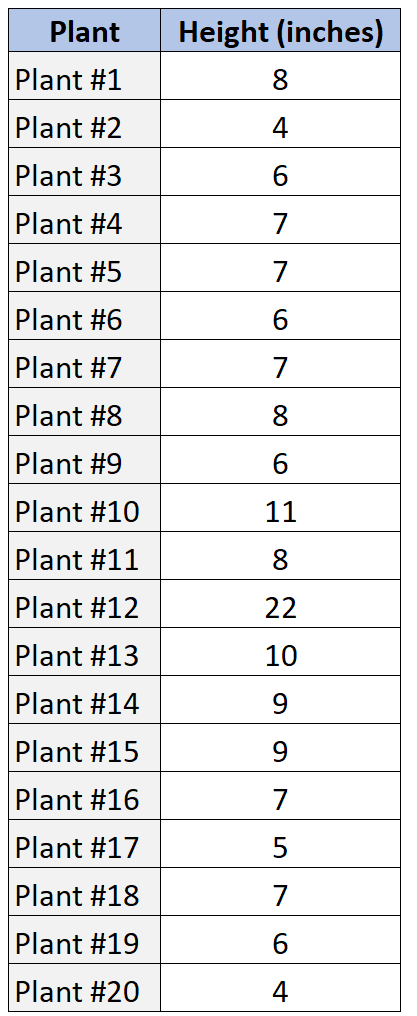
Veri değerlerinin bu dağılımını tanımlamak için SOCS’yi şu şekilde kullanabiliriz.

Şekil

Öncelikle dağılımın şeklini açıklamak istiyoruz.

Dağıtımın şeklini görselleştirmenin yararlı bir yolu, veri kümesindeki her bir değerin frekansını görüntüleyen bir histogram oluşturmaktır:

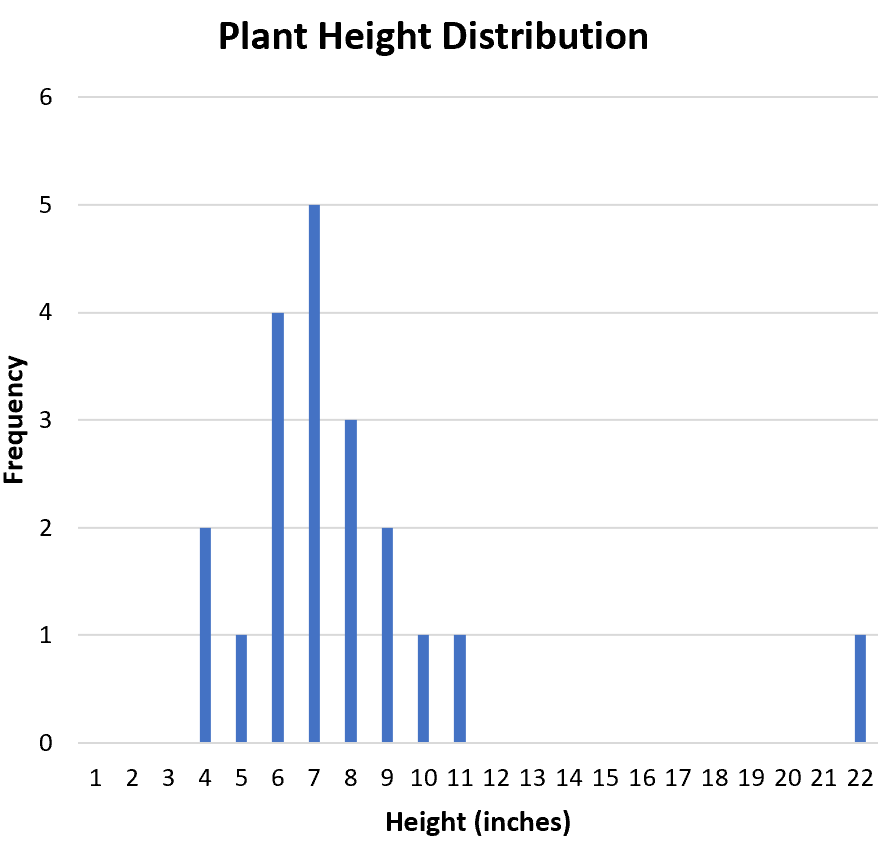
Dağılım simetrik mi yoksa bir tarafa çarpık mı?   Histogramdan dağılımın yaklaşık olarak simetrik olduğunu görebiliriz. Başka bir deyişle değerler öyle ya da böyle önyargılı değildir.

Dağılım tek modlu mu (tek tepe) yoksa çift modlu mu (iki tepe)? Dağıtım tek modludur. “7” değerinde bir zirveye sahiptir.

Aykırı Değerler

Daha sonra veri setinde herhangi bir aykırı değer olup olmadığını belirlemek istiyoruz. Histogramdan dağılımı görsel olarak inceleyebiliriz ve 22’nin potansiyel olarak aykırı bir değer olduğunu görebiliriz:

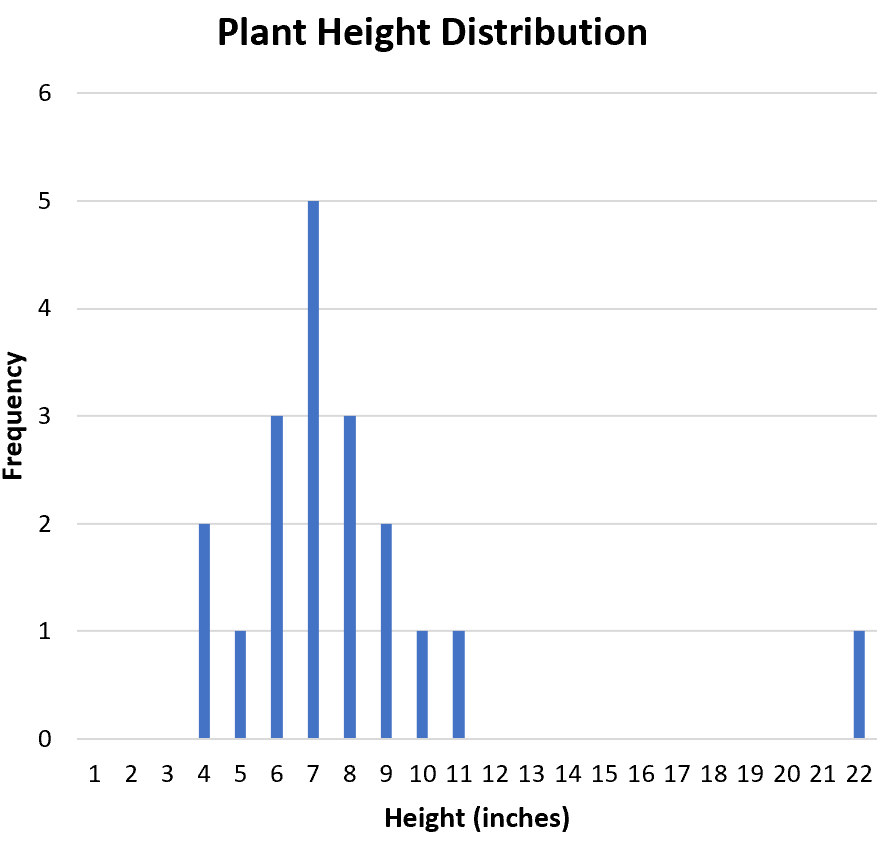
Aykırı değeri resmi olarak tanımlamanın yaygın bir yolu, üçüncü çeyreğin üzerinde veya birinci çeyreğin altında çeyrekler arası aralığın 1,5 katı olan herhangi bir değerdir.

Çeyrekler arası aralık hesaplayıcıyı kullanarak 20 ham veri değerini girebiliriz ve üçüncü çeyreğin 9 , çeyrekler arası aralığın 3 olduğunu ve dolayısıyla 9 + (1,5*3) = 13,5’ten büyük herhangi bir değerin aykırı değer olduğunu görebiliriz, tanımı gereği.

22, 13,5’tan büyük olduğundan 22’yi aykırı değer olarak ilan edebiliriz.

Merkez

Daha sonra dağılımın merkezinin nerede olduğunu açıklamak istiyoruz. Kullanabileceğimiz üç yaygın merkezi eğilim ölçüsü ortalama, medyan ve moddur.

Ortalama: Bu, dağılımın ortalama değeridir. Bunu, tüm bireysel değerleri toplayıp ardından toplam değer sayısına bölerek buluruz:

Ortalama = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Medyan: Bu, dağılımın “ortalama” değeridir. Tüm değerleri en küçükten en büyüğe sıralayıp ardından medyan değerini belirleyerek bunu buluyoruz. 7 olduğu ortaya çıktı.

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Mod: En sık görülen değerdir. 7 olduğu ortaya çıktı.

Yaymak

Daha sonra dağılımdaki değerlerin dağılımını açıklamak istiyoruz. Kullanabileceğimiz dört yaygın dağılım ölçüsü aralık, kareler arası aralık, standart sapma ve varyanstır.

Aralık: Veri setindeki en büyük değer ile en küçük değer arasındaki farktır. Bunun 22 – 4 = 18 olduğu ortaya çıkıyor.

Çeyrekler Arası Aralık: Veri değerlerinin ortadaki %50’sinin genişliğini ölçer. 20 ham veri değerini çeyrekler arası aralık hesaplayıcıya girdiğimizde bunun 3’e eşit olduğunu görebiliriz.

Standart sapma: Bu, veri değerlerinin ortalama dağılımının bir ölçüsüdür. 20 ham veri değerini varyans ve standart sapma hesaplayıcısına girdiğimizde standart sapmanın 3,69’a eşit olduğunu görebiliriz.

Varyans: Bu basitçe standart sapmanın karesidir. Bu 3,69 ² = 13,63’e eşittir.

Çözüm

SOCS’yi rehber olarak kullanarak bitki boyu dağılımını şu şekilde tanımlayabildik:

• Dağılım tek modlu ve simetrikti, yani tek bir tepe noktası vardı ve bir tarafa ya da diğerine çarpık değildi.
• Dağıtımın bir aykırı değeri vardı: 22.
• Dağılımın ortalaması 7,85, ortancası 7 ve modu 7 idi.
• Dağılımın aralığı 18, çeyrekler arası aralığı 3, standart sapması 3,69 ve varyansı 13,63’tü.

Herhangi bir dağıtımı tanımlamak için SOCS’yi kullanabileceğimizi unutmayın; bu, bir dağılımın şeklini, aykırı değerlerinin olup olmadığını, merkezin yaklaşık olarak nerede olduğunu ve Verilerin değerlerinin nasıl dağıtılacağını tam olarak anlamamız için yararlı bir yoldur. öyle.