İstatistikler neden önemlidir? (i̇statistiğin önemli olmasının 10 nedeni!)

İstatistik alanı verilerin toplanması, analizi, yorumlanması ve sunumuyla ilgilidir.

Teknoloji günlük hayatımızda giderek daha fazla yer aldıkça, insanlık tarihinde daha önce hiç olmadığı kadar fazla veri üretiliyor ve toplanıyor.

İstatistikler, aşağıdaki görevleri gerçekleştirmek için bu verileri nasıl kullanacağımızı anlamamıza yardımcı olabilecek alandır:

• Etrafımızdaki dünyayı daha iyi anlıyoruz.
• Verileri kullanarak kararlar alın.
• Verileri kullanarak gelecekle ilgili tahminlerde bulunun.

Bu yazımızda istatistik alanının modern yaşamda bu kadar önemli olmasının 10 nedenini paylaşıyoruz.

Sebep 1: Dünyayı anlamak için tanımlayıcı istatistikleri kullanın

Tanımlayıcı istatistikler bir ham veri parçasını tanımlamak için kullanılır. Tanımlayıcı istatistiklerin üç ana türü vardır:

• Özet istatistikler
• Grafik
• Masalar

Bu öğelerin her biri mevcut verileri daha iyi anlamamıza yardımcı olabilir.

Örneğin belli bir şehirdeki 10.000 öğrencinin sınav puanlarını gösteren ham bir veri setimiz olduğunu varsayalım. Tanımlayıcı istatistikleri şu amaçlarla kullanabiliriz:

• Ortalama test puanını ve test sonuçlarının standart sapmasını hesaplayın.
• Test sonuçlarının dağılımını görselleştirmek için bir histogram veya kutu grafiği oluşturun.
• Test sonuçlarının dağılımını anlamak için bir frekans tablosu oluşturun.

Tanımlayıcı istatistikleri kullanarak öğrencilerin test puanlarını ham verilere bakmaktan çok daha kolay bir şekilde anlayabiliriz.

Sebep 2: Yanıltıcı grafiklere dikkat edin

Dergilerde, medyada, çevrimiçi makalelerde ve dergilerde giderek daha fazla grafik üretiliyor. Ne yazık ki, temel verileri anlamadığınız takdirde grafikler genellikle yanıltıcı olabilir.

Örneğin, bir derginin belirli bir üniversitedeki öğrencilerin GPA ve ACT puanları arasında negatif bir korelasyon bulan bir araştırma yayınladığını varsayalım.

Ancak bu negatif korelasyon, hem GPA hem de ACT puanı yüksek olan öğrencilerin elit bir üniversiteye gidebilmesi, GPA ve ACT puanı düşük olan öğrencilerin ise hiç kabul edilmemesi nedeniyle ortaya çıkmaktadır.

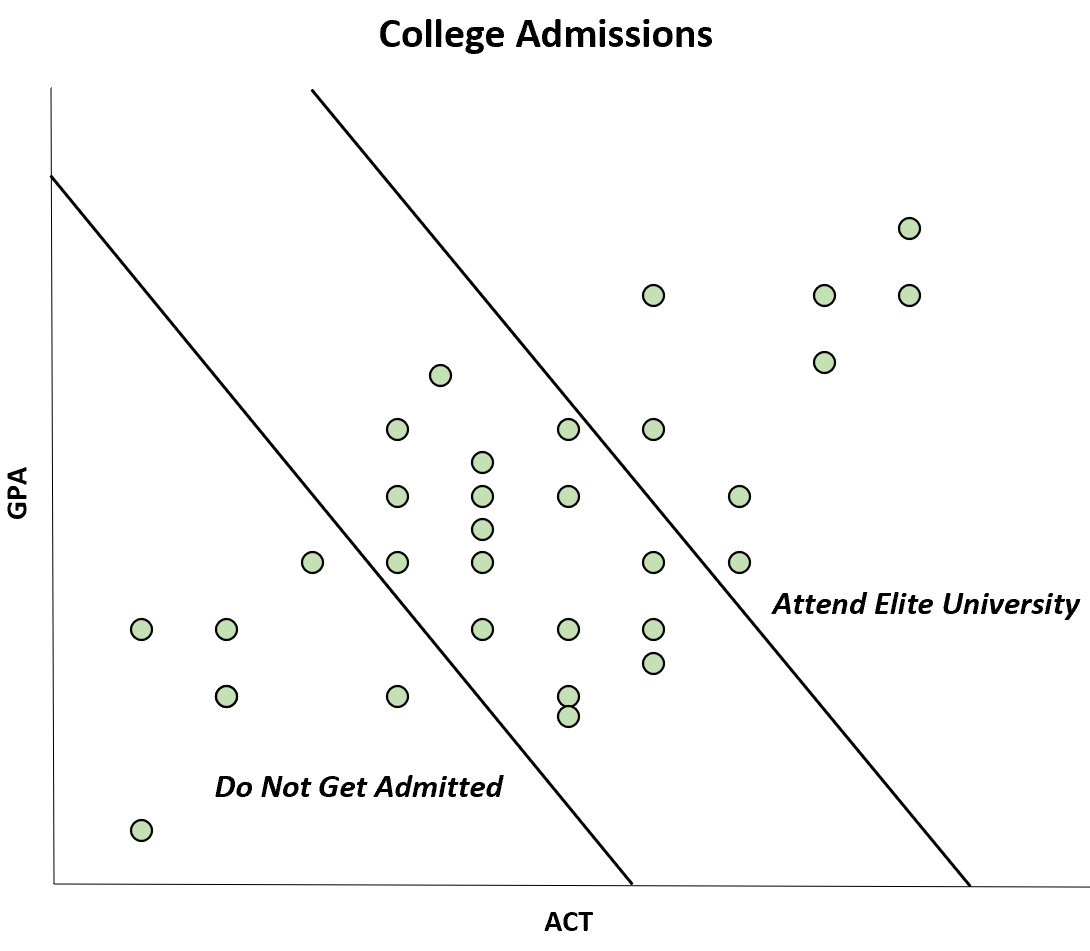
ACT ile GPA arasındaki korelasyon evrende pozitif olmasına rağmen örneklemde negatif görünmektedir.

Bu özel önyargı Berkson önyargısı olarak bilinir. Bu önyargının farkında olarak bazı grafiklerin sizi yanıltmasını önleyebilirsiniz.

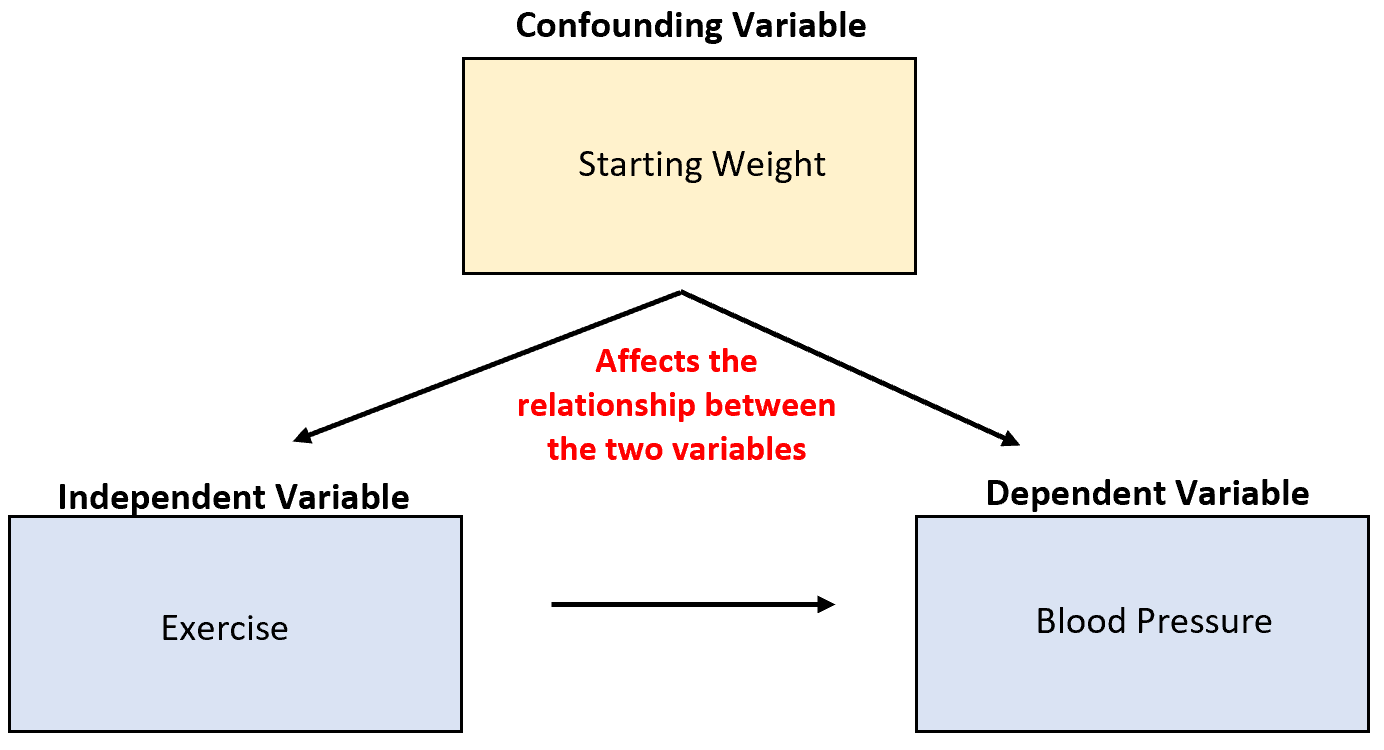
Sebep 3: Kafa karıştırıcı değişkenlere karşı dikkatli olun

İstatistikte öğreneceğiniz önemli bir kavram da kafa karıştırıcı değişkenler kavramıdır.

Bunlar dikkate alınmayan değişkenlerdir ve deneyin sonuçlarını karıştırıp güvenilmez sonuçlara yol açabilirler.

Örneğin, bir araştırmacının dondurma satışları ve köpekbalığı saldırıları hakkında veri topladığını ve iki değişkenin yüksek oranda ilişkili olduğunu keşfettiğini varsayalım. Bu, artan dondurma satışlarının daha fazla köpekbalığı saldırısına neden olduğu anlamına mı geliyor?

Olası değil. Bunun en olası nedeni kafa karıştırıcı sıcaklık değişkenidir. Dışarısı sıcak olduğunda daha çok insan dondurma alır ve daha çok insan okyanusa gider.

Sebep 4: olasılıkları kullanarak daha iyi kararlar vermek

İstatistiğin en önemli alt alanlarından biri olasılıktır . Olayların meydana gelme olasılığını inceleyen alandır.

Olasılıkla ilgili temel bir anlayışa sahip olarak gerçek dünyada daha bilinçli kararlar verebilirsiniz.

Örneğin, bir lise öğrencisinin belirli bir üniversiteye kabul edilme şansının %10 olduğunu bildiğini varsayalım. Bu öğrenci “en az bir” geçme olasılığı formülünü kullanarak başvurduğu en az bir üniversiteye kabul edilme olasılığını bulabilir ve başvuracağı üniversite sayısını sonuca göre ayarlayabilir.

Sebep 5: Araştırmada P-değerlerini Anlamak

İstatistikte öğreneceğiniz bir diğer önemli kavram da p değerleridir .

Bir p değerinin klasik tanımı şöyledir:

P değeri, sıfır hipotezinin doğru olduğu göz önüne alındığında, en az örnek istatistiğiniz kadar uç bir örnek istatistiği gözlemleme olasılığıdır.

Örneğin, bir fabrikanın ortalama ağırlığı 200 pound olan lastikler ürettiğini iddia ettiğini varsayalım. Bir denetçi, bu tesiste üretilen lastiklerin gerçek ortalama ağırlığının 200 pound farklı olduğunu öne sürüyor. Böylece bir hipotez testi yapar ve testin p değerinin 0,04 olduğunu bulur.

Bu p değerini şu şekilde yorumlayabilirsiniz:

Fabrika gerçekten ortalama ağırlığı 200 pound olan lastikler üretiyorsa, tüm denetimlerin %4’ü, rastgele örnekleme hatası nedeniyle numunede gözlemlenen etkiyi veya daha fazlasını elde edecektir. Bu bize, fabrikanın ortalama ağırlığı 200 pound olan lastikleri gerçekten üretmesi durumunda denetçi tarafından elde edilen örnek verilerin elde edilmesinin oldukça nadir olacağını söylüyor.

Bu nedenle denetçi, bu tesiste üretilen lastiklerin gerçek ortalama ağırlığının gerçekte 200 pound olduğuna ilişkin boş hipotezi muhtemelen reddedecektir.

Sebep 6: Korelasyonu anlayın

İstatistikte öğreneceğiniz bir diğer önemli kavram da iki değişken arasındaki doğrusal ilişkiyi bize anlatan korelasyondur .

Korelasyon katsayısının değeri her zaman -1 ile 1 arasındadır; burada:

• -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
• 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
• 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir

Bu değerleri anlayarak gerçek dünyadaki değişkenler arasındaki ilişkiyi anlayabilirsiniz.

Örneğin reklam harcaması ile gelir arasındaki korelasyon 0,87 ise iki değişken arasında güçlü bir pozitif ilişki olduğunu anlayabilirsiniz. Reklama daha fazla para harcadıkça gelirinizde öngörülebilir bir artış bekleyebilirsiniz.

Sebep 7: Gelecekle ilgili tahminlerde bulunun

İstatistik öğrenmenin bir diğer önemli nedeni de aşağıdaki gibi temel regresyon modellerini anlamaktır:

• Basit doğrusal regresyon
• Çoklu doğrusal gerileme
• Lojistik regresyon

Bu modellerin her biri, modeldeki belirli yordayıcı değişkenlerin değerine dayalı olarak bir yanıt değişkeninin gelecekteki değeri hakkında tahminlerde bulunmanıza olanak tanır.

Örneğin şirketler gerçek dünyada yaş, gelir, etnik köken vb. gibi belirleyici değişkenleri kullanırken her zaman birden fazla doğrusal regresyon modeli kullanır. mağazalarında kaç müşterinin harcama yapacağını tahmin etmek.

Benzer şekilde lojistik şirketleri de toplam talep, nüfus büyüklüğü vb. gibi tahmin değişkenlerini kullanır. gelecekteki satışları tahmin etmek.

Hangi alanda çalışırsanız çalışın, regresyon modellerinin gelecekteki bir olguyu tahmin etmek için kullanılma ihtimali yüksektir.

Sebep 8: Çalışmalardaki potansiyel önyargıyı anlayın

İstatistik çalışmanın bir başka nedeni de gerçek dünya çalışmalarında ortaya çıkabilecek tüm farklı önyargı türlerinin farkında olmaktır.

İşte bazı örnekler:

• Önyargıyı gözlemleyin
• Kendi kendine seçim önyargısı
• Referans önyargısı
• İhmal edilen değişken önyargı
• Eksik sayma önyargısı
• Yanıt vermeme önyargısı

Bu tür önyargılara ilişkin temel bir anlayışa sahip olarak, araştırma yaparken bu önyargılardan kaçınabilir veya diğer araştırma makalelerini veya çalışmalarını okurken bunların farkında olabilirsiniz.

Sebep 9: İstatistiksel testlerin yaptığı varsayımları anlayın

Birçok istatistiksel test, incelenen temel veriler hakkında varsayımlarda bulunur.

Bir çalışmanın sonuçlarını okurken veya hatta kendi çalışmanızı yürütürken, sonuçların güvenilir olması için hangi varsayımların yapılması gerektiğini anlamak önemlidir.

Aşağıdaki makaleler, yaygın olarak kullanılan birçok istatistiksel test ve prosedürde yapılan varsayımları paylaşmaktadır:

• İstatistikte eşit varyans varsayımı nedir?
• İstatistikte normallik varsayımı nedir?
• İstatistikte bağımsızlık varsayımı nedir?

Sebep 10: Aşırı genellemeyi önlemek

İstatistik çalışmanın bir başka nedeni de aşırı genelleme kavramını anlamaktır.

Bu, bir çalışmaya katılan bireylerin genel popülasyondaki bireyleri temsil etmediği ve dolayısıyla bir çalışmanın bulgularının tüm popülasyona genellenmesinin uygun olmadığı durumlarda ortaya çıkar.

Örneğin, belirli bir okuldaki öğrencilerin yüzde kaçının en sevdikleri film türü olarak “drama”yı tercih ettiğini bilmek istediğimizi varsayalım. Toplam öğrenci nüfusunun %50’si erkek ve %50’si kızlardan oluşuyorsa, bu durumda %90’ı erkek ve %10’u kızlardan oluşan bir örneklem, önemli ölçüde daha az sayıda erkek çocuğun favori tür olarak tiyatroyu tercih etmesi durumunda taraflı sonuçlara yol açabilir.

İdeal olarak, örneğimizin popülasyonumuzun “mini versiyonuna” benzemesini istiyoruz. Dolayısıyla, eğer genel öğrenci nüfusunun %50’si kızlardan ve %50’si erkeklerden oluşuyorsa, örneklemimiz %90’ı erkek ve yalnızca %10’u kızlardan oluşuyorsa temsili olmayacaktır.

Bu nedenle, ister kendi anketinizi yapıyor olun ister bir anketin sonuçlarını okuyor olun, örnek verilerin toplam nüfusu temsil edip etmediğini ve anket sonuçlarının nüfusa güvenle genelleştirilip genelleştirilemeyeceğini anlamak önemlidir.

Ek kaynaklar

İstatistiklere girişteki en önemli kavramlara ilişkin temel bir anlayış kazanmak için aşağıdaki makalelere göz atın:

Tanımlayıcı veya çıkarımsal istatistikler
Nüfus vs. örnek
İstatistikler ve parametreler
Niteliksel ve niceliksel değişkenler
Ölçüm seviyeleri: nominal, sıralı, aralık ve oran