Sıra (istatistik)

Bu yazımızda istatistikte aralığın ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Bir veri kümesinin kapsamına ilişkin çözülmüş bir alıştırma bulacaksınız ve son olarak bunun ne için olduğunu ve ne zaman kullanılması gerektiğini size göstereceğiz.

İstatistikte aralık nedir?

İstatistikte aralık, bir numunenin verilerinin maksimum değeri ile minimum değeri arasındaki farkı gösteren bir dağılım ölçüsüdür. Bu nedenle, bir popülasyonun veya istatistiksel örneklemin kapsamını hesaplamak için maksimum değerin minimum değerden çıkarılması gerekir.

Örneğin bir veri setinin maksimum değeri 9, minimum değeri 2 ise bu istatistiksel örneğin aralığı 7’dir (9-2=7).

İstatistiksel aralığa ölçüm kapsamı veya aralığı da denir.

Yani aralık, varyans, standart sapma (veya standart sapma), ortalama sapma ve değişim katsayısı ile birlikte bir dağılım ölçüsüdür.

İstatistiklerde aralık nasıl hesaplanır

Bir numunenin aralığı, istatistiksel numune verilerinin uç değerlerinin çıkarılmasıyla hesaplanır, yani bir numunenin aralığı, tüm verilerin maksimum değeri eksi minimum değere eşittir .

Bu nedenle, bir veri kümesinin istatistiksel aralığını hesaplama formülü şöyledir:

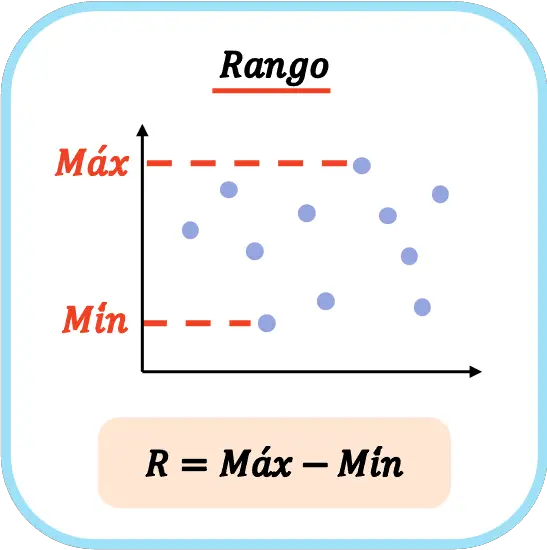
İstatistiklerde, büyük R sembolü genellikle bir veri serisinin kapsamını belirtmek için kullanılır.

Bu nedenle bir veri kümesinin aralığını hesaplamak oldukça basittir çünkü yalnızca uç değerler arasındaki farkı belirlemeniz gerekir. Dikkat etmeniz gereken tek şey maksimum ve minimum verileri doğru almak ve hiçbir rakamı unutmamaktır.

Örnek aralık (istatistik)

İstatistiklerde aralığın tanımını gördükten sonra, aşağıda bir veri kümesi aralığının nasıl elde edildiğini görebilmeniz için çalışılmış bir örnek verilmiştir.

• Bir şirket, amiral gemisi ürününün son yirmi yılda elde ettiği satışları istatistiksel olarak analiz etmek istiyor. Bunu yapmak için sizden sıralama dahil çeşitli istatistiksel ölçümleri hesaplamanızı istiyorlar. Ürünün satışları aşağıdaki tabloda görüldüğü gibi ise bu veri setinin aralığı nedir?

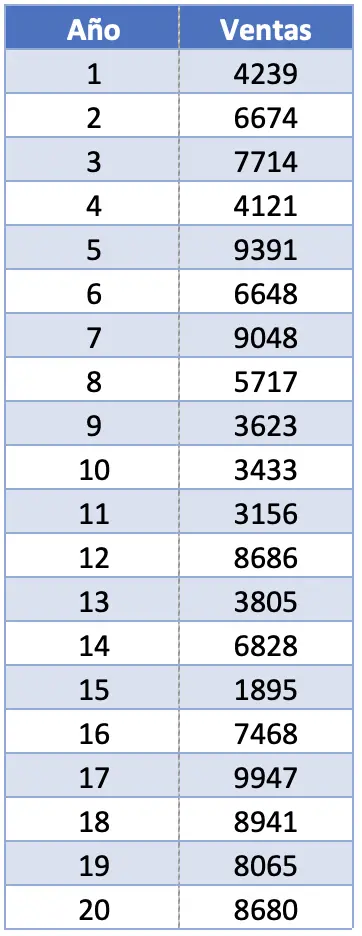
Bu alıştırmada 20 gözlemimiz var. Gerçekte, toplam gözlem sayısı, bir numunenin kapsamının hesaplanmasında hiçbir fark yaratmaz çünkü biz yalnızca en büyük değer ve en küçük değerle ilgileniriz.

Bu nedenle, bu istatistiksel örneğin kapsamını bulmak için yukarıda görülen formülü kullanmalıyız.

Aralığın maksimum değeri satılan 9947 adet, minimum değeri ise 1895’tir. Dolayısıyla veri setinin aralığını bulmak için bu iki değeri çıkarmamız gerekiyor:

Bu da son birkaç yılda satışlardaki maksimum değişimin 8.052 adet olduğu anlamına geliyor. Aşağıda tüm egzersiz verilerini istatistiksel aralıklarıyla birlikte grafiksel olarak görebilirsiniz; grafik muhtemelen aralığın anlamını anlamanıza yardımcı olacaktır.

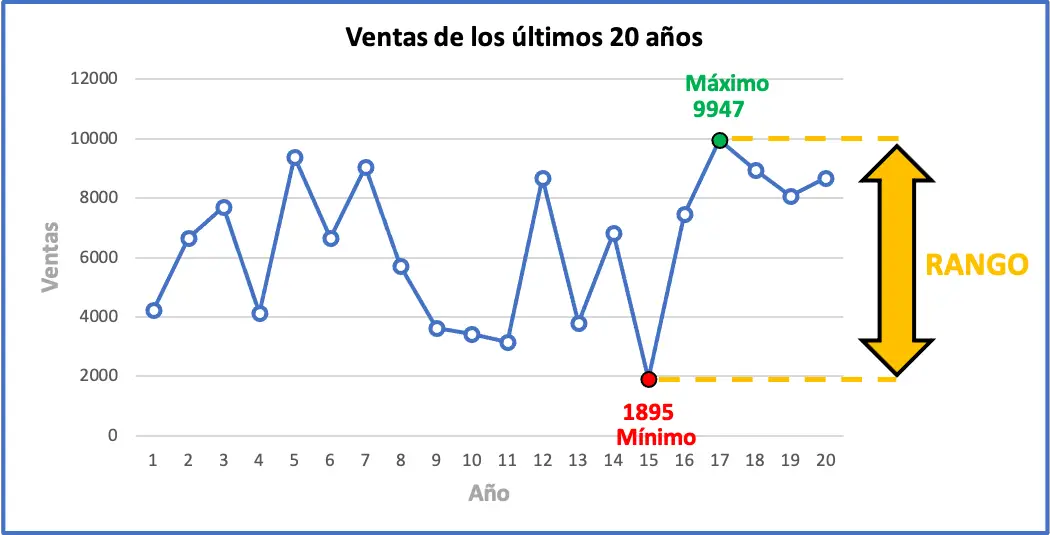
İstatistiksel aralık ne için kullanılır?

İstatistikte kapsam kavramını anlamayı tamamlamak için, bunun ne için kullanıldığını ve bu dağılım ölçüsünün nasıl yorumlanacağını göreceğiz.

İstatistiklerde aralık, bir veri kümesinin maksimum değeri ile minimum değeri arasındaki farkı gösterir. Bu nedenle aralık, bir veri kümesinin toplam dağılımını belirtmek için kullanılan bir ölçüdür .

Bir veri kümesinin aralık değerini bildiğinizde, o kümedeki herhangi iki gözlem arasındaki maksimum farkı da bilirsiniz, böylece verilerin dağınık mı yoksa birbirine yakın mı olduğu konusunda fikir edinebilirsiniz. Genel olarak aralığın mümkün olduğu kadar az olması avantajlıdır çünkü bu, çok az dağılım olduğu ve dolayısıyla hesaplamaların daha doğru olacağı anlamına gelir.

Örneğin aralık, iki farklı örnek arasında karşılaştırma yapılmasına olanak sağlayan bir ölçüm olabilir çünkü örneklerin dağılımları hakkında fikir edinmenizi sağlar.

Ancak istatistiksel aralığın yorumlanmasında yanıltıcı olabileceğinden dikkatli olunmalıdır. Bir veri kümesinin aslında çok düşük bir dağılımı olabilir, ancak örnek içinde bir aykırı değer varsa, aralık çok geniş olacak ve bu nedenle örneğin dağılımını doğru şekilde yansıtmayacaktır.

Ayrıca değerleri onluk mertebesinde olan bir numunenin sıralamasının 5 olması ile değerleri binlik mertebesinde olan bir numunenin aynı sıralamaya sahip olması aynı değildir. Mantıksal olarak her iki aralık aynı sayıya sahip olsa bile ilk örnek ikinciye göre çok daha fazla dağılmıştır.

Sonuç olarak aralık, bir veri kümesinin dağılımını analiz etmek için yararlı bir istatistiksel ölçüdür, ancak verileri doğru şekilde yorumlamak için diğer ölçümlerin de hesaplanması gerekir.