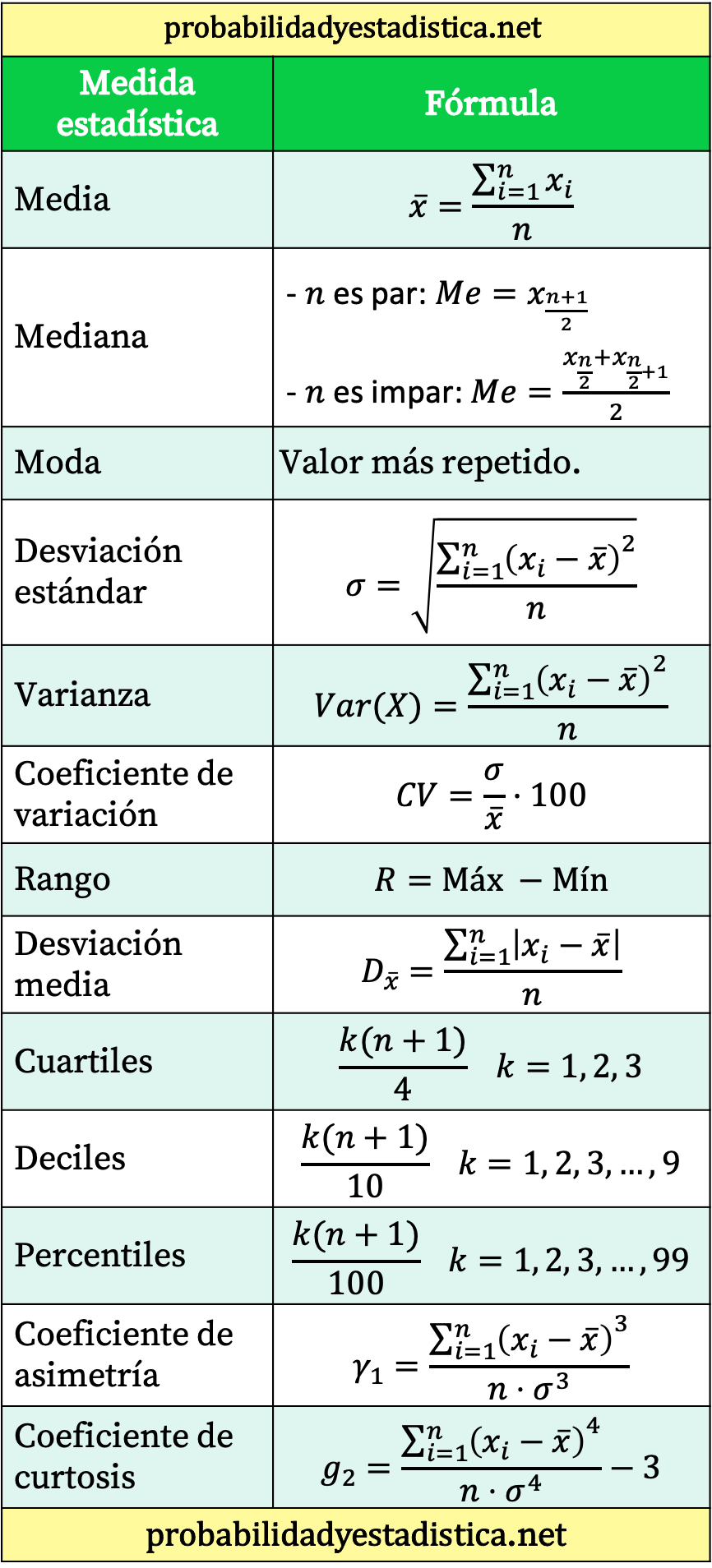
İstatistiksel formüller

İle Dr.benjamin anderson Ağustos 1, 2023 İstatistik 0 Yorum

Burada temel istatistiksel formülleri bulacaksınız. Ayrıca sizi, her istatistiksel formülün uygulama örneklerini görebileceğiniz ve ayrıca hesaplamaları yapmak zorunda kalmamak ve formülün sonucunu doğrudan öğrenmek için çevrimiçi bir hesap makinesi kullanabileceğiniz makalelerimize bağlantı olarak bırakıyoruz.

Merkezi eğilimin istatistiksel ölçümleri için formüller

Yarım

Ortalamayı hesaplamak için tüm değerleri toplayın ve ardından toplam veri sayısına bölün. Ortalamanın formülü bu nedenle aşağıdaki gibidir:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

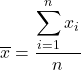
İstatistiklerde ortalama, aritmetik ortalama veya ortalama olarak da bilinir.

➤ Bakınız: Aritmetik Ortalama Hesaplayıcı

Medyan

Medyan , en küçükten en büyüğe doğru sıralanan tüm verilerin ortadaki değeridir. Başka bir deyişle medyan sıralı veri setini iki eşit parçaya böler.

Medyanın hesaplanması, toplam veri sayısının çift veya tek olmasına bağlıdır:

Toplam veri sayısı tek ise medyan verinin tam ortasında kalan değer olacaktır. Yani sıralanan verinin (n+1)/2 konumundaki değeri.

$Me=x_{\frac{n+1}{2}$

Toplam veri noktası sayısı çift ise medyan, merkezde bulunan iki veri noktasının ortalaması olacaktır. Yani sıralı verinin n/2 ve n/2+1 konumlarında bulunan değerlerin aritmetik ortalamasıdır.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Altın

$n$

örnekteki toplam veri sayısıdır ve Me simgesi medyanı gösterir.

➤ Bakınız: Medyan hesaplayıcı

Moda

İstatistikte mod , veri kümesindeki mutlak frekansı en yüksek olan değerdir, yani mod, bir veri kümesinde en çok tekrarlanan değerdir.

Bu nedenle, mod için özel bir formül yoktur, ancak istatistiksel bir veri kümesinin modunu hesaplamak için, her veri öğesinin örnekte kaç kez göründüğünü saymanız yeterlidir; en çok tekrarlanan veriler mod olacaktır.

Modun istatistiksel mod veya modal değer olduğu da söylenebilir.

➤ Bakınız: Moda hesaplayıcısı

İstatistiksel dağılım ölçümleri için formüller

Standart sapma

Standart sapma olarak da adlandırılan standart sapma, veri serisindeki sapmaların karelerinin toplamının karekökünün toplam gözlem sayısına bölünmesine eşittir.

Bu nedenle standart sapmanın formülü şu şekildedir:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Bakınız: Standart sapma hesaplayıcısı

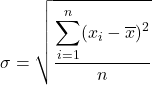
Varyans

Varyans , toplam gözlem sayısına göre artıkların karelerinin toplamına eşittir. Dolayısıyla bu istatistiksel ölçümün formülü aşağıdaki gibidir:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Altın:

$X$

varyansını hesaplamak istediğiniz rastgele değişkendir.
$x_i$

veri değeri

$i$

.
$n$

toplam gözlem sayısıdır.
$\overline{X}$

rastgele değişkenin ortalamasıdır

$X$

.

➤ Bakınız: Boşluk hesaplayıcı

Değişim katsayısı

İstatistikte varyasyon katsayısı , bir veri kümesinin ortalamasına göre dağılımını belirlemek için kullanılan bir dağılım ölçüsüdür. Değişim katsayısı, verinin standart sapmasının ortalamasına bölünmesi ve ardından değerin yüzde olarak ifade edilmesi için 100 ile çarpılmasıyla hesaplanır.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Bakınız: Değişim katsayısı hesaplayıcısı

Düzenli

İstatistiksel aralık, bir örnekteki verilerin maksimum değeri ile minimum değeri arasındaki farkı gösteren bir dağılım ölçüsüdür. Bu nedenle, bir popülasyonun veya istatistiksel örneklemin kapsamını hesaplamak için maksimum değerin minimum değerden çıkarılması gerekir.

$R=\text{M\'ax}-\text{M\'in}$

➤ Bakınız: İstatistiksel aralık örneği

Çeyrekler arası aralık

Çeyrekler arası aralık olarak da adlandırılan çeyrekler arası aralık, üçüncü ve birinci çeyrekler arasındaki farkı gösteren istatistiksel dağılım ölçüsüdür.

Bu nedenle, bir istatistiksel veri setinin çeyrekler arası aralığını hesaplamak için önce üçüncü ve birinci çeyrekleri bulmanız ve ardından bunları çıkarmanız gerekir.

$IQR=Q_3-Q_1$

➤ Bakınız: Çeyrekler Arası Aralık Hesaplayıcı

orta fark

Ortalama mutlak sapma olarak da adlandırılan ortalama sapma, mutlak sapmaların ortalamasıdır. Bu nedenle ortalama sapma, her veri öğesinin aritmetik ortalamadan sapmalarının toplamının veri öğelerinin toplam sayısına bölünmesine eşittir.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Bakınız: Ortalama sapma hesaplayıcısı

İstatistiksel konum ölçümleri için formüller

çeyrekler

İstatistikte çeyrekler , sıralı bir veri kümesini dört eşit parçaya bölen üç değerdir. Böylece birinci, ikinci ve üçüncü çeyrekler tüm istatistiksel verilerin sırasıyla %25, %50 ve %75’ini temsil etmektedir.

Çeyrekler büyük Q ve çeyrek endeksi ile temsil edilir, dolayısıyla ilk çeyrek Q ₁ , ikinci çeyrek Q ₂ ve üçüncü çeyrek Q _3’tür .

Çeyrek formülü şöyledir:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Lütfen unutmayın: Bu formül bize çeyreğin değerini değil çeyreğin konumunu söyler. Çeyrek, formül tarafından elde edilen konumda bulunan veriler olacaktır.

Ancak bazen bu formülün sonucu bize ondalık bir sayı verecektir. Bu nedenle sonucun ondalık sayı olup olmamasına bağlı olarak iki durumu birbirinden ayırmamız gerekir:

Formülün sonucu ondalık kısmı olmayan bir sayı ise çeyrek, yukarıdaki formülün sağladığı konumdaki verilerdir.
Formül sonucu ondalık kısmı olan bir sayıysa çeyrek değeri aşağıdaki formül kullanılarak hesaplanır:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Burada x _i ve x _i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.

➤ Bakınız: Çeyrek Hesaplayıcı

ondalık dilimler

İstatistikte ondalık sayılar , sıralı bir veri kümesini on eşit parçaya bölen dokuz değerdir. Böylece birinci, ikinci, üçüncü,… ondalık dilim numunenin veya popülasyonun %10, %20, %30,…’unu temsil eder.

Ondalık dilimler büyük D harfi ve ondalık indeks ile temsil edilir, yani ilk ondalık dilim D ₁ , ikinci ondalık dilim D ₂ , üçüncü ondalık dilim D ₃ vb.

Ondalık formül aşağıdaki gibidir:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Lütfen unutmayın: Bu formül bize ondalık dilimin değerini değil, ondalık dilimin konumunu söyler. Ondalık kısım, formül tarafından elde edilen konumda bulunan veriler olacaktır.

Ancak bazen bu formülün sonucu bize ondalık sayı verir, bu nedenle sonucun ondalık sayı olup olmadığına bağlı olarak iki durumu ayırmamız gerekir:

Formülün sonucu ondalık kısmı olmayan bir sayı ise, ondalık kısım yukarıdaki formülün sağladığı konumda bulunan verilerdir.
Formülün sonucu ondalık kısmı olan bir sayı ise, ondalık değer aşağıdaki formül kullanılarak hesaplanır:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Burada x _i ve x _i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.

➤ Bakınız: Ondalık hesaplayıcı

yüzdelikler

İstatistikte yüzdelikler , sıralı bir veri kümesini yüz eşit parçaya bölen değerlerdir. Yani yüzdelik dilim, veri kümesinin belirli bir yüzdesinin altına düştüğü değeri belirtir.

Yüzdelikler büyük harf P ve yüzdelik endeksi ile temsil edilir, yani ilk yüzdelik dilim P ₁ , 40. yüzdelik dilim P ₄₀ , 79. yüzdelik dilim P ₇₉ vb.

Yüzdelik formül şöyledir:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Lütfen unutmayın: Bu formül bize yüzdelik dilimin konumunu belirtir, ancak değerini vermez. Yüzdelik dilim, formülün elde ettiği konumda bulunan veriler olacaktır.

Ancak bazen bu formülün sonucu bize ondalık sayı verir, bu nedenle sonucun ondalık sayı olup olmadığına bağlı olarak iki durumu ayırmamız gerekir:

Formülün sonucu ondalık kısmı olmayan bir sayı ise yüzdelik dilim yukarıdaki formülün sağladığı konumdaki verilere karşılık gelir.
Formül sonucu ondalık kısmı olan bir sayıysa , tam yüzdelik değer aşağıdaki formül kullanılarak hesaplanır:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Burada x _i ve x _i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.

➤ Bakınız: Yüzdelik Hesaplayıcı

İstatistiksel şekil ölçüm formülleri

asimetri katsayısı

Çarpıklık katsayısı veya çarpıklık endeksi, bir dağılımın çarpıklığını belirlemek için kullanılan istatistiksel bir katsayıdır. Yani asimetri katsayısını hesaplayarak, dağılımın asimetri türünü, bunun grafiksel bir gösterimini yapmaya gerek kalmadan öğrenebilirsiniz.

Asimetri katsayısının formülü aşağıdaki gibidir:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Eşdeğer olarak, Fisher asimetri katsayısını hesaplamak için aşağıdaki iki formülden herhangi biri kullanılabilir:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

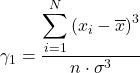
Altın

$E$

matematiksel beklenti,

$\overline{x}$

aritmetik ortalama,

$\sigma$

standart sapma ve

$n$

toplam veri sayısı.

➤ Bakınız: Asimetri katsayısı

basıklık katsayısı

Keskinlik olarak da adlandırılan basıklık, bir dağılımın ortalama etrafında ne kadar yoğunlaştığını gösterir. Başka bir deyişle basıklık, bir dağılımın dik mi yoksa düz mü olduğunu gösterir. Spesifik olarak, bir dağılımın basıklığı ne kadar büyük olursa, o kadar dik (veya daha keskin) olur.

Basıklık katsayısının formülü aşağıdaki gibidir:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

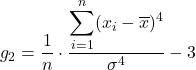
Altın

$x_i$

gözleme karşılık gelen değerdir

$i$

$\overline{x}$

aritmetik ortalama,

$\sigma$

standart sapma ve

$n$

toplam veri sayısı.

➤ Bakınız: Düzleştirme Katsayısı Hesaplayıcısı

Tüm istatistiksel formüllerin özet tablosu

Son olarak size temel istatistiksel formülleri özetleyen bir tablo bırakıyoruz.

➤ Bakınız: Olasılık formülleri

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Merkezi eğilimin istatistiksel ölçümleri için formüller

Yarım

Medyan

Moda

İstatistiksel dağılım ölçümleri için formüller

Standart sapma

Varyans

Değişim katsayısı

Düzenli

Çeyrekler arası aralık

orta fark

İstatistiksel konum ölçümleri için formüller

çeyrekler

ondalık dilimler

yüzdelikler

İstatistiksel şekil ölçüm formülleri

asimetri katsayısı

basıklık katsayısı

Tüm istatistiksel formüllerin özet tablosu

yazar hakkında

Dr.benjamin anderson

Yorum ekle