Moda (istatistikler)

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makalede istatistiklerde hangi modun olduğu açıklanmaktadır. Gruplandırılmış veriler ve gruplanmamış veriler için istatistiksel modu nasıl bulacağınızı, farklı mod türlerini ve bu istatistiksel ölçümün birkaç örneğini öğreneceksiniz.

İstatistiklerde mod nedir?

İstatistikte mod, veri kümesindeki mutlak frekansı en yüksek olan değerdir, yani mod, bir veri kümesinde en çok tekrarlanan değerdir.

Bu nedenle, istatistiksel bir veri kümesinin modunu hesaplamak için, her veri öğesinin örnekte kaç kez göründüğünü saymanız yeterlidir; en çok tekrarlanan veri, mod olacaktır.

Mod, istatistiksel bir dağılımı tanımlamak için kullanılır, çünkü en çok tekrarlanan değer genellikle dağılımın merkezindedir.

Modun istatistiksel mod veya modal değer olduğu da söylenebilir. Benzer şekilde, veriler aralıklar halinde gruplandırıldığında en çok tekrarlanan aralık, modal aralık veya modal sınıftır .

Genel olarak Mo terimi istatistiksel modun sembolü olarak kullanılır; örneğin X dağıtım modu Mo(X)’tür.

Modun, medyan ve ortalamanın yanı sıra merkez konumun da istatistiksel bir ölçüsü olduğunu unutmayın. Aşağıda bu istatistiksel önlemlerin her birinin ne anlama geldiğini göreceğiz.

İstatistiklerdeki mod türleri

İstatistiklerde, en çok tekrarlanan değerlerin sayısına göre sınıflandırılan çeşitli mod türleri vardır:

Tek modlu mod : Maksimum tekrar sayısına sahip yalnızca bir değer vardır. Örneğin, [1, 4, 2, 4, 5, 3].
Bimodal mod : Maksimum tekrar sayısı iki farklı değerde gerçekleşir ve her iki değer de aynı sayıda tekrarlanır. Örneğin, [2, 6, 7, 2, 3, 6, 9].
Multimodal mod : Üç veya daha fazla değer aynı maksimum tekrar sayısına sahiptir. Örneğin, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

İstatistiksel mod nasıl bulunur?

Bir veri kümesinin istatistiksel modunu bulmak için aşağıdaki adımları izlemelisiniz:

Verileri sıraya koyun. Bu adım zorunlu değildir ancak sayıları saymayı kolaylaştıracaktır.
Her sayının kaç kez göründüğünü sayın.
En sık görünen sayı istatistiksel moddur.

İstatistiksel mod örnekleri

Modanın istatistiklerdeki tanımı göz önüne alındığında, kavramı daha iyi anlayabilmeniz için aşağıda her moda türünün bir örneğini görebilirsiniz.

Tek modlu mod örneği

Aşağıdaki veri kümesinin modu nedir?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

Rakamlar sıralanmamıştır, bu nedenle modu bulmayı kolaylaştırmak için önce onları sıralayacağız.

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

2 ve 9 sayıları iki kez görünüyor, ancak 5 sayısı üç kez tekrarlanıyor. Bu nedenle veri serisinin modu 5 numaradır.

$Mo=5$

İki modlu mod örneği

Aşağıdaki veri setinin modunu hesaplayın:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

İlk önce sayıları sıraya koyuyoruz:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

Gördüğünüz gibi 6 sayısı ve 8 sayısı toplamda dört kez karşımıza çıkıyor, bu da maksimum tekrar sayısıdır. Bu nedenle, bu durumda bu iki modlu bir moddur ve iki sayı, veri kümesinin modudur:

$Mo=\{ 6 \ ; \ 8\}$

Çok modlu mod örneği

Aşağıdaki veri kümesi modunu bulun:

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

Çok fazla veri olduğundan, saymayı kolaylaştırmak için önce bunları artan düzende sıralıyoruz:

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

En çok tekrarlanan sayılar 20, 27 ve 31’dir, her üç sayı da beşer kez tekrarlanır. Bu örneğin modu bu nedenle çok modludur.

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

moda hesap makinesi

Modunu hesaplamak için herhangi bir istatistiksel örnekten verileri aşağıdaki çevrimiçi hesap makinesine girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Gruplandırılmış veriler için mod

Verileri aralık şeklinde gruplandırdığımızda, her bir veri parçasının kaç kez tekrarlandığını gerçekten bilmiyoruz, yalnızca her aralığın sıklığını biliyoruz.

Bu nedenle, aralıklara göre gruplandırılmış verilerin modunu hesaplamak için aşağıdaki formülü kullanmamız gerekir :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

Altın:

L _i , modal aralığın alt sınırıdır (en yüksek mutlak frekans aralığı).
f _i modal aralığın mutlak frekansıdır.
f _i-1 modaldan önceki aralığın mutlak frekansıdır.
f _i+1 modaldan sonraki aralığın mutlak frekansıdır.
A _i modal aralığın genişliğidir.

Örnek olarak, aşağıda aralıklara göre gruplandırılmış veri modunun hesaplandığı bir alıştırmayı çözdünüz:

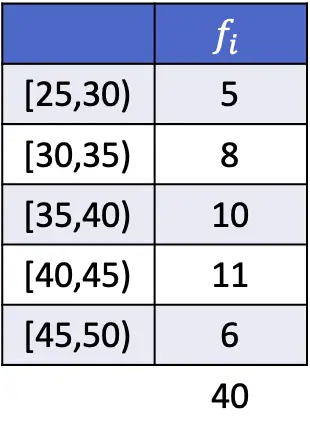
gruplandırılmış veriler için istatistiksel mod örneği

Bu durumda modal aralık, en büyük mutlak frekansa sahip aralık olduğundan [40,45] olur. Bu nedenle, gruplandırılmış veriler için mod formülü parametreleri şunlardır:

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

Bu nedenle aralıklara göre gruplandırılmış verilerin modunu belirlemek için formülü uyguluyoruz ve hesaplamayı yapıyoruz:

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

Mod, ortalama ve medyan arasındaki fark

Bu son bölümde mod, ortalama ve medyan arasındaki farkın ne olduğunu göreceğiz. Her üçü de merkezi konumun istatistiksel ölçüleri olduğundan anlamları farklıdır.

Makale boyunca açıklandığı gibi matematikte mod, bir veri setinde en çok tekrarlanan değerdir.

İkincisi, ortalama tüm istatistiksel verilerin ortalama değeridir. Bu nedenle, belirli verilerin ortalamasını elde etmek için tüm verileri toplamanız ve ardından sonucu gözlem sayısına bölmeniz gerekir.

Ve son olarak medyan, veriler sıralandığında merkezi konumu işgal eden değerdir.

Böylece, üç istatistiksel ölçü bir olasılık dağılımının tanımlanmasına yardımcı olur çünkü merkezi değerleri hakkında bir fikir sağlarlar. Ancak unutmayın ki hiçbir ölçü diğerinden daha iyi değildir, bunlar sadece farklı kavramları ifade etmektedir.

Moda özellikleri

Moda özellikleri şunlardır:

Mod hem niceliksel değişkenlerde hem de niteliksel değişkenlerde bulunabilir.
Rastgele bir değişkene doğrusal dönüşüm uygularsak uygulanan işlemlere bağlı olarak ortalamanın değeri değişecektir.

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

Genel olarak mod aykırı değerlere karşı duyarsızdır.
Tüm değerler aynı frekansa sahipse mod yoktur.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil