İstatistiklerde artıklar nelerdir?

Artık ,regresyon analizinde gözlemlenen bir değer ile tahmin edilen bir değer arasındaki farktır.

Aşağıdaki şekilde hesaplanır:

Artık = Gözlemlenen değer – Tahmin edilen değer

Doğrusal regresyonun amacının, bir veya daha fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek olduğunu hatırlayın. Bunu yapmak için doğrusal regresyon, en küçük kareler regresyon çizgisi adı verilen, verilere en iyi “uyan” çizgiyi bulur.

Bu çizgi, veri setindeki her gözlem için bir tahmin üretir ancak regresyon çizgisi tarafından yapılan tahminin, gözlemlenen değerle tam olarak eşleşmesi pek olası değildir.

Tahmin ile gözlemlenen değer arasındaki fark artıktır. Gözlemlenen değerleri çizer ve uygun regresyon çizgisini üst üste koyarsak, her gözlem için artıklar, gözlem ile regresyon çizgisi arasındaki dikey mesafe olacaktır:

Bir gözlemin değeri, regresyon çizgisi tarafından tahmin edilen değerden büyükse, pozitif bir artık değeri vardır.

Tersine, eğer değeri regresyon çizgisi tarafından tahmin edilen değerden küçükse, bir gözlemin negatif bir kalıntısı vardır.

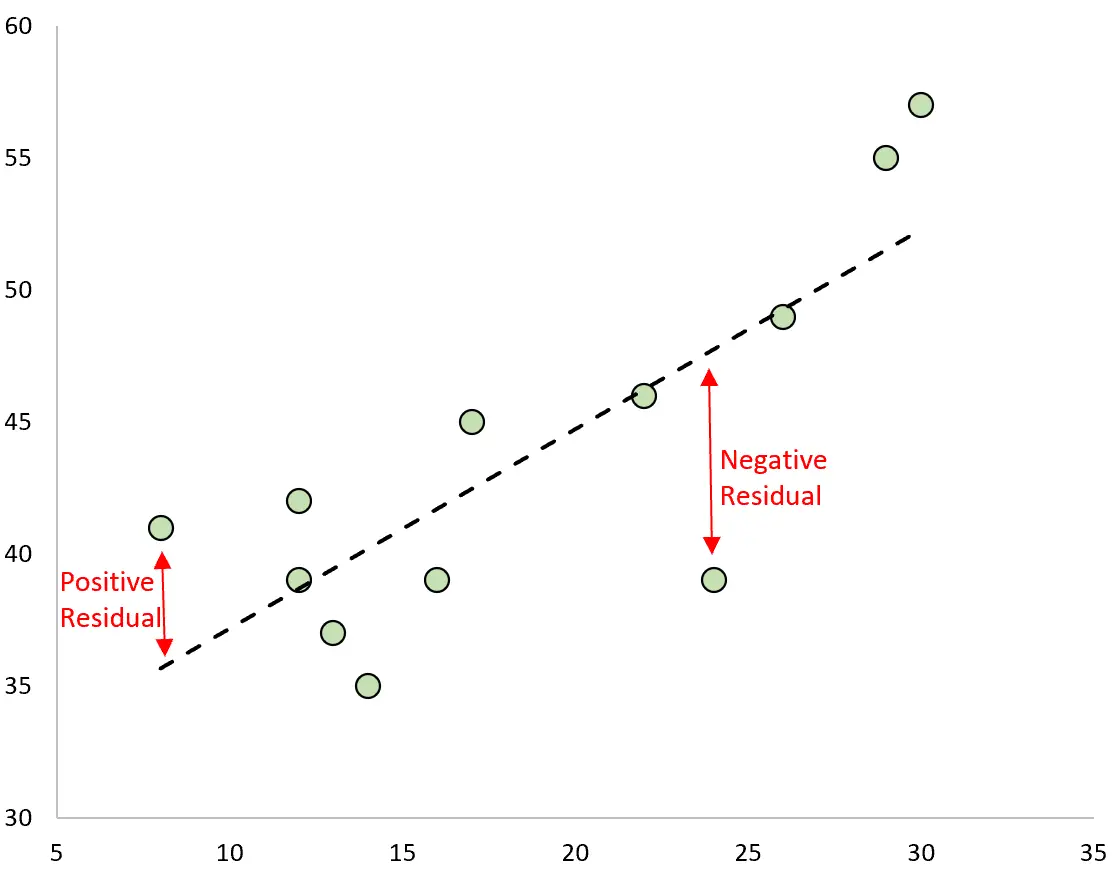
Bazı gözlemlerin pozitif artıkları olacak, bazılarının ise negatif artıkları olacak, ancak tüm artıkların toplamı sıfıra eşit olacak.

Artıkların hesaplanmasına örnek

Toplamda 12 gözlem içeren aşağıdaki veri setine sahip olduğumuzu varsayalım:

Bu veri setine doğrusal bir regresyon çizgisi sığdırmak için istatistiksel yazılım ( R , Excel , Python , Stata vb. gibi) kullanırsak, en uygun çizginin şu şekilde ortaya çıktığını göreceğiz:

y = 29,63 + 0,7553x

Bu satırı kullanarak X değerine göre her Y değeri için tahmin edilen değeri hesaplayabiliriz. Örneğin ilk gözlemin tahmin edilen değeri şöyle olacaktır:

y = 29,63 + 0,7553*(8) = 35,67

Daha sonra bu gözlemin artığı şu şekilde hesaplayabiliriz:

Artık = Gözlemlenen değer – Tahmin edilen değer = 41 – 35,67 = 5,33

Her gözlem için artık değeri bulmak amacıyla bu işlemi tekrarlayabiliriz:

Gözlemleri uygun regresyon çizgisiyle görselleştirmek için bir dağılım grafiği oluşturursak, bazı gözlemlerin çizginin üstünde, diğerlerinin ise çizginin altında olduğunu göreceğiz:

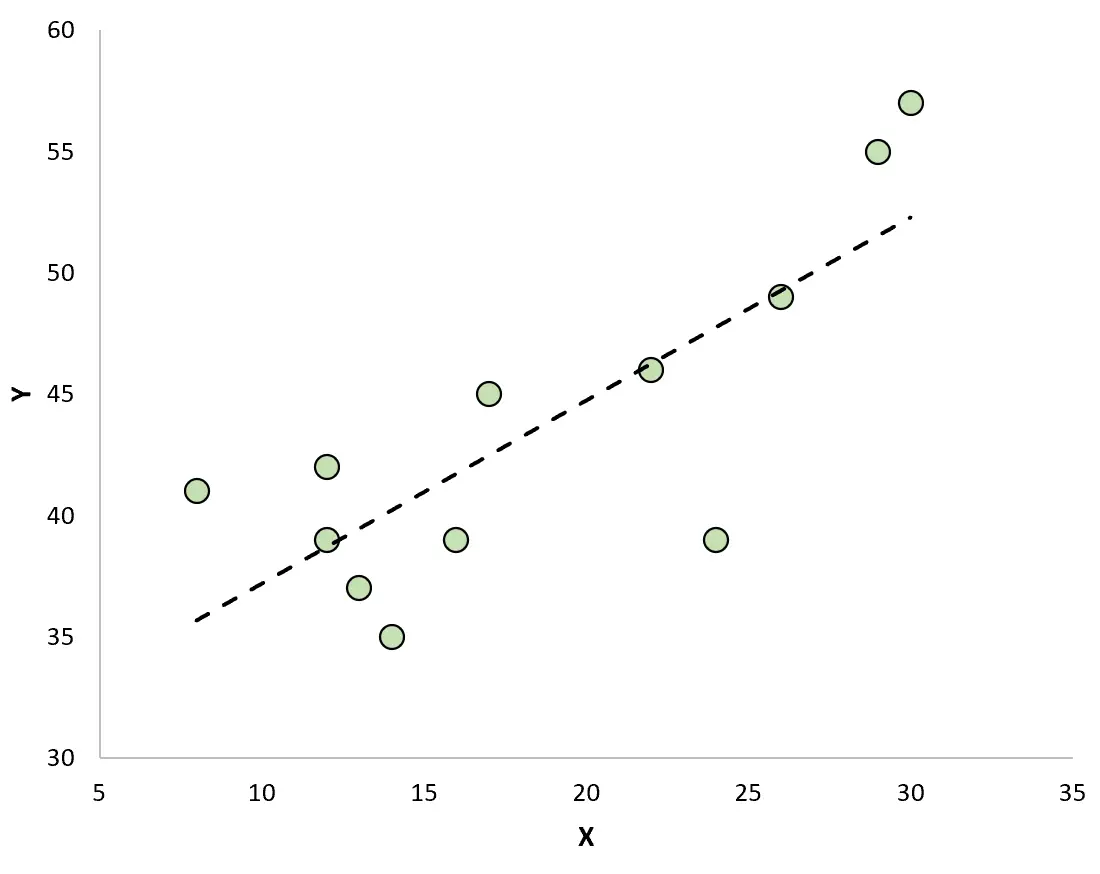
Kalıntıların özellikleri

Kalıntılar aşağıdaki özelliklere sahiptir:

• Bir veri setindeki her gözlemin karşılık gelen bir kalıntısı vardır. Yani, eğer bir veri seti toplamda 100 gözlem içeriyorsa, model 100 tahmin edilen değer üretecek ve sonuçta toplamda 100 artık elde edilecektir.
• Tüm artıkların toplamı sıfırdır.
• Artıkların ortalama değeri sıfırdır.

Kalıntılar pratikte nasıl kullanılır?

Uygulamada regresyonda artıklar üç farklı nedenden dolayı kullanılır:

1. Modelin yeterliliğini değerlendirin.

Uygun bir regresyon çizgisi ürettiğimizde, tüm karelerin toplamı olan artık kareler toplamını (RSS) hesaplayabiliriz. RSS ne kadar düşük olursa, regresyon modeli verilere o kadar iyi uyar.

2. Normallik varsayımını kontrol edin.

Doğrusal regresyonun temel varsayımlarından biri artıkların normal dağıldığıdır.

Bu hipotezi test etmek için, bir modelin artıklarının normal dağılıma uyup uymadığını belirlemek için kullanabileceğimiz bir grafik türü olan QQ grafiğini oluşturabiliriz.

Grafikteki noktalar kabaca düz bir çapraz çizgi oluşturuyorsa normallik varsayımı karşılanmıştır.

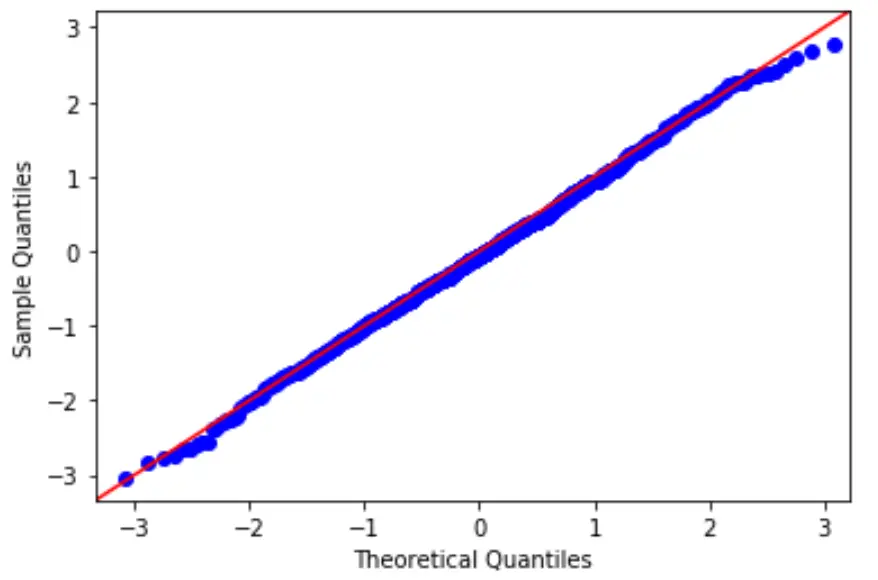
3. Eş varyans varsayımını kontrol edin.

Doğrusal regresyonun diğer bir temel varsayımı, artıkların her x seviyesinde sabit varyansa sahip olmasıdır. Buna homoskedastisite denir. Durum böyle olmadığında, artıklar değişen varyanstan muzdariptir.

Bu varsayımın karşılanıp karşılanmadığını kontrol etmek için, artıkları modelin tahmin edilen değerlerine göre gösteren bir dağılım grafiği olan bir artıklar grafiği oluşturabiliriz.

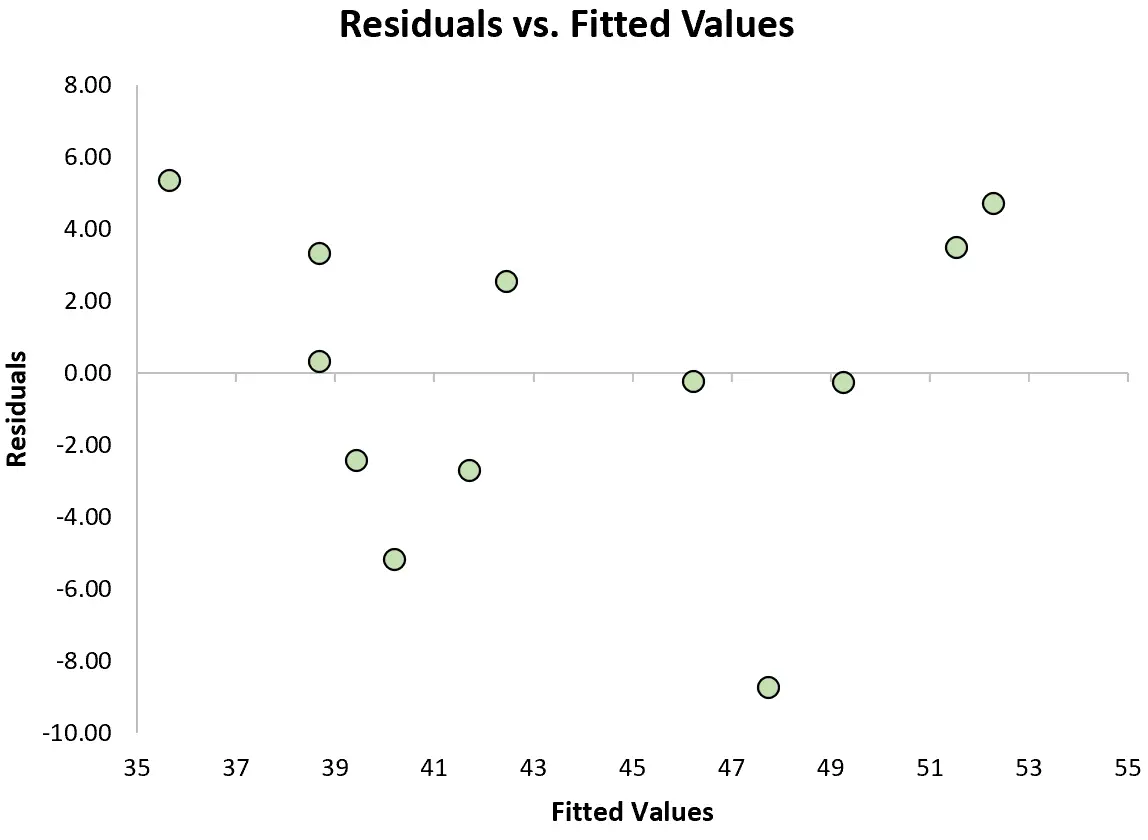
Eğer artıklar grafikte net bir trend olmadan yaklaşık olarak sıfır etrafında eşit bir şekilde dağılmışsa, o zaman genellikle eşvaryans varsayımının karşılandığını söyleriz.

Ek kaynaklar

Basit Doğrusal Regresyona Giriş
Çoklu Doğrusal Regresyona Giriş
Doğrusal regresyonun dört varsayımı
Excel’de Artık Grafik Nasıl Oluşturulur