Sas'ta roc eğrisi nasıl oluşturulur

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullanabileceğimiz bir yöntemdir.

Lojistik regresyon modelinin bir veri kümesine ne kadar iyi uyduğunu değerlendirmek için aşağıdaki iki ölçüme bakabiliriz:

• Duyarlılık: Sonuç gerçekten olumluyken modelin bir gözlem için olumlu bir sonuç tahmin etme olasılığı. Buna aynı zamanda “gerçek pozitif oran” da denir.
• Özgüllük: Sonuç gerçekten negatif olduğunda modelin bir gözlem için negatif bir sonuç öngörme olasılığı. Buna aynı zamanda “gerçek negatif oran” da denir.

Bu iki ölçümü görselleştirmenin bir yolu, “alıcı çalışma karakteristiği” eğrisi anlamına gelen bir ROC eğrisi oluşturmaktır. Bu, lojistik regresyon modelinin duyarlılığını ve özgüllüğünü gösteren bir grafiktir.

Aşağıdaki adım adım örnek, SAS’ta bir ROC eğrisinin nasıl oluşturulacağını ve yorumlanacağını gösterir.

1. Adım: Veri kümesini oluşturun

Öncelikle 18 öğrenci için aşağıdaki değişkenlere ilişkin bilgileri içeren bir veri seti oluşturacağız:

• Belirli bir üniversiteye kabul (1 = evet, 0 = hayır)
• GPA (1’den 4’e kadar ölçek)
• ACT puanı (1’den 36’ya kadar ölçek)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

Adım 2: Lojistik regresyon modelini yerleştirin ve bir ROC eğrisi oluşturun

Daha sonra, yanıt değişkeni olarak “kabul”ü ve yordayıcı değişkenler olarak “gpa” ve “hareket”i kullanarak lojistik regresyon modeline uyacak şekilde proc lojistiğini kullanacağız.

SAS’ın yanıt değişkeninin 1 değerini alma olasılığını nasıl tahmin edeceğini bilmesi için azalmayı belirteceğiz.

Modelin ROC eğrisini oluşturmak için de graphs(only)=roc kullanacağız:

 /*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
  model acceptance = gpa act;
run ;

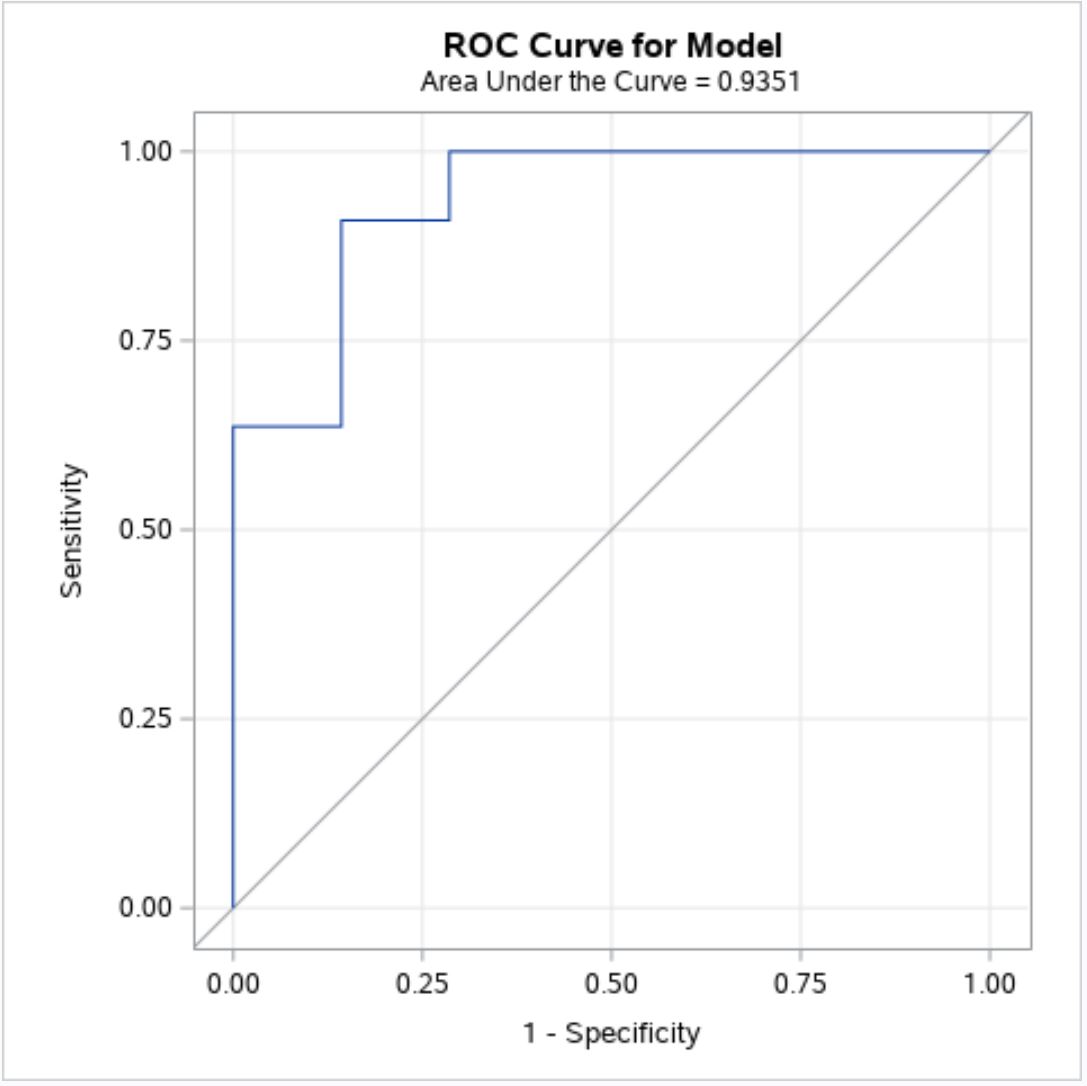
Adım 3: ROC eğrisini yorumlayın

ROC eğrisi grafiğin sol üst köşesine ne kadar yakın olursa, model veri setindeki yanıt değerlerinin değerini o kadar iyi tahmin eder.

Yukarıdaki grafikten mavi ROC eğrisinin sol üst köşeye sarılma eğiliminde olduğunu görebiliriz, bu da lojistik regresyon modelinin yanıt değerlerinin değerini tahmin etme konusunda iyi bir iş çıkardığını gösterir.

Lojistik regresyon modelinin verilere ne kadar iyi uyduğunu ölçmek için, grafiğin ne kadarının eğrinin altında olduğunu bize söyleyen AUC’yi (eğri altındaki alan) hesaplayabiliriz.

AUC 1’e ne kadar yakınsa model o kadar iyidir. AUC değeri 0,5’e eşit olan bir model, rastgele sınıflandırma yapan bir modelden daha iyi değildir.

Yukarıdaki grafik başlığı altında bu modelin AUC’sinin 0,9351 olduğunu görebiliyoruz.

Bu değerin bire yakın olması modelin yanıt değerlerinin değerini iyi tahmin ettiğini doğrulamaktadır.

AUC değerini farklı lojistik regresyon modellerinin uyumunu karşılaştırmak için de kullanabiliriz.

Örneğin, iki farklı lojistik regresyon modelini uydurduğumuzu ve her biri için AUC değerlerini hesapladığımızı varsayalım:

• Model 1’in AUC’si: 0,9351
• Model 2’nin AUC’si: 0,8140

Model 1’in AUC’si daha büyük olduğundan, bu bize Model 1’in verileri uydurma konusunda Model 2’den daha iyi bir iş çıkardığını gösterir.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer yaygın işlemlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta basit doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta çoklu doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta lojistik regresyon nasıl gerçekleştirilir?